Exercice : DM 2022 :Produit Scalaire
Exercice 1
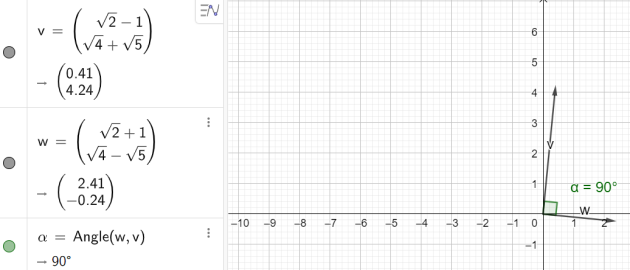
Dans un repère orthonormé \((O ;\vec{i} ;\vec{j})\),on considère les vecteurs \(\vec{v}\) de coordonnées \(\left( \begin{array}{c} \sqrt{2} – 1 \\ \sqrt{4} +\sqrt{5} \end{array} \right)\) et \(\vec{w}\) de coordonnées \(\left( \begin{array}{c} \sqrt{2}+ 1 \\ \sqrt{4} –\sqrt{5} \end{array} \right)\) ?
Question
Les vecteurs \(\vec{v}\) et \(\vec{w}\) sont-ils orthogonaux ?
Solution
\(\vec{v}.\vec{w}= \left( \begin{array}{c} \sqrt{2} – 1 \\ \sqrt{4} +\sqrt{5} \end{array} \right). \left( \begin{array}{c} \sqrt{2}+ 1 \\ \sqrt{4} –\sqrt{5} \end{array} \right)\)
\(\iff \vec{v}.\vec{w}=(\sqrt{2}^2 – 1^2)+ ( \sqrt{4}^2 -\sqrt{5}^2)\)
\(\iff \vec{v}.\vec{w}=(2 – 1)+ (4 -5)\)
\(\iff \vec{v}.\vec{w}=(1)+ (-1)=0\)
donc les vecteurs \(\vec{v}\) et \(\vec{w}\) sont orthogonaux.
Exercice 2
Soit \((O ;\vec{i} ;\vec{j})\) un repère orthonormé. Soient les vecteurs \(\vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=a^2\vec{u}+a\vec{i}\)
Question
1.Faire une figure dans le cas où \(a=2\)
Solution
\(\vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=2^2\vec{u}+2\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=4\vec{u}+2\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=4(3\vec{j}-\vec{i})+2\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=12\vec{j}-4\vec{i}+2\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=12\vec{j}-2\vec{i}\)
\(\iff \vec{u}=-\vec{i}+3\vec{j}\) et \(\vec{v}=-2\vec{i}+12\vec{j}\)
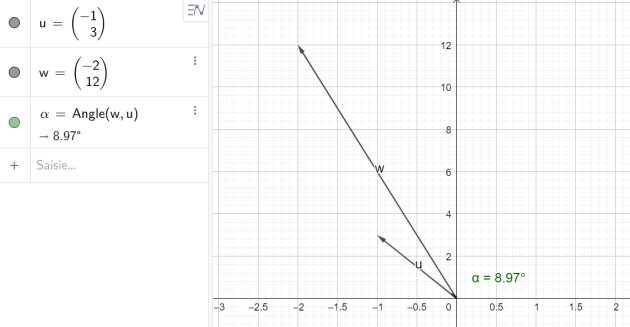
donc \(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -2 \\ 12 \end{array} \right)\)
Question
2.Donner les coordonnées des vecteurs \(\vec{u}\) et \(\vec{v}\) dans le repère \((O ;\vec{i} ;\vec{j})\)
En particulier, montrer que les coordonnées du vecteur \(\vec{v}\) sont :
\(\left( \begin{array}{c}-a^2+a\\3a^2\end{array} \right)\)
Solution
\(\vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=a^2\vec{u}+a\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=a^2(3\vec{j}-\vec{i})+a\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=3a^2\vec{j}-a^2\vec{i}+a\vec{i}\)
\(\iff \vec{u}=3\vec{j}-\vec{i}\) et \(\vec{v}=3a^2\vec{j}+(-a^2+a)\vec{i}\)
\(\iff \vec{u}=-\vec{i}+3\vec{j}\) et \(\vec{v}=(-a^2+a)\vec{i}+3a^2\vec{j}\)
donc \(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -a^2+a \\ 3a^2 \end{array} \right)\)
Question
3.Pour quelles valeurs du réel \(a\), les vecteurs \(\vec{u}\) et \(\vec{v}\) sont-ils orthogonaux ?
Faire une figure pour la valeur de \(a\) non nulle.
Solution
\(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -a^2+a \\ 3a^2 \end{array} \right)\)
\(\vec{u}.\vec{v}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right).\left( \begin{array}{c} -a^2+a \\ 3a^2 \end{array} \right)\)
\(\iff \vec{u}.\vec{v}=(– 1 \times (-a^2+a)+ 3 \times 3a^2 )\)
\(\iff \vec{u}.\vec{v}=(a^2-a+9a^2)\)
\(\iff \vec{u}.\vec{v}=10a^2-a\)
Les vecteurs \(\vec{u}.\vec{v}\) sont orthogonaux
si et seulement si \(\vec{u}.\vec{v}=0\)
\(\iff 10a^2-a=0\)
\(\iff a(10a-1)=0\)
\(\color{red}{\text{Propriété :}}\)
\(\color{red}{\text{Un produit de facteurs est nul}}\)
\(\color{red}{\text{si et seulement si }}\)
\(\color{red}{\text{un des facteurs au moins est nul.}}\)
donc les vecteurs \(\vec{u}.\vec{v}\) sont orthogonaux
si et seulement si \(a=0\) ou \(10a-1=0\)
\(\iff a=0 \quad ou \quad 10a=1\)
\(\iff a=0 \quad ou \quad a=\frac{1}{10}\)
\(\iff a=0 \quad ou \quad a=0,1\)
\(\color{magenta}{\text{Pour a=0:}}\)
\(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -0^2+0 \\ 3 \times 0^2 \end{array} \right)\)
\(\iff\) \(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} 0 \\ 0 \end{array} \right)\)
Le vecteur \(\vec{v}=\vec{0}\)
donc le vecteur \(\vec{v}\) est orthogonal au vecteur \(\vec{u}\)
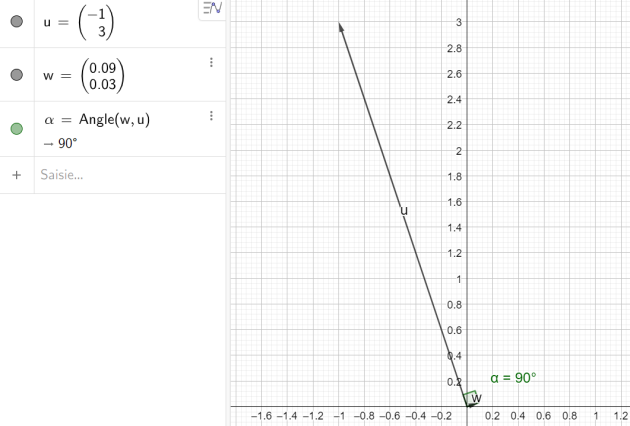
Pour \(a=0,1\):
\(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -0,1^2+0,1 \\ 3 \times 0,1^2 \end{array} \right)\)
\(\iff\) \(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} -0,01+0,1 \\ 3 \times 0,01 \end{array} \right)\)
\(\iff\) \(\vec{u}=\left( \begin{array}{c} – 1 \\ 3 \end{array} \right)\)
et \(\vec{v}=\left( \begin{array}{c} 0,09 \\ 0,03 \end{array} \right)\)
Exercice 3
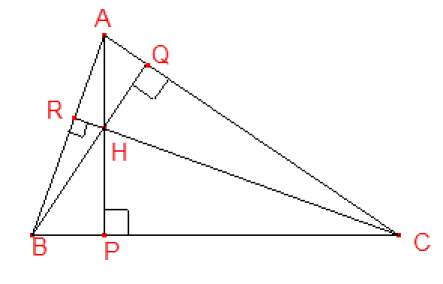
Soit H l'orthocentre du triangle ABC et P,Q et R les pieds des hauteurs (voir figure ci-contre).
Question
Justifier, sans aucun calcul, chacune des égalités suivantes :
\(\vec{HP}.\vec{HA}=\vec{HB}.\vec{HA}=\vec{HB}.\vec{HQ}=\vec{HB}.\vec{HC}=\vec{HR}.\vec{HC}\)
Solution
Le projeté orthogonal :
- du point B sur la droite (HA) est le point P
- du point H sur la droite (HA) est le point H
donc le projeté orthogonal du vecteur \(\vec{HB}\) sur le vecteur \(\vec{HA}\) est le vecteur \(\vec{HP}\)
d'où \(\vec{HB}.\vec{HA}=\vec{HP}.\vec{HA}\)
Le projeté orthogonal :
- du point A sur la droite (HB) est le point Q
- du point H sur la droite (HB) est le point H
donc le projeté orthogonal du vecteur \(\vec{HA}\) sur le vecteur \(\vec{HB}\) est le vecteur \(\vec{HQ}\)
d'où \(\vec{HB}.\vec{HA}=\vec{HB}.\vec{HQ}\)
Le projeté orthogonal :
- du point C sur la droite (HB) est le point Q
- du point H sur la droite (HB) est le point H
donc le projeté orthogonal du vecteur \(\vec{HC}\) sur le vecteur \(\vec{HB}\) est le vecteur \(\vec{HQ}\)
d'où \(\vec{HB}.\vec{HQ}=\vec{HB}.\vec{HC}\)
Le projeté orthogonal :
- du point B sur la droite (HB) est le point R
- du point H sur la droite (HB) est le point H
donc le projeté orthogonal du vecteur \(\vec{HB}\) sur le vecteur \(\vec{HB}\) est le vecteur \(\vec{HR}\)
d'où \(\vec{HB}.\vec{HC}=\vec{HR}.\vec{HC}\)
Exercice 3
Soit \((O ;\vec{i} ;\vec{j})\) un repère orthonormé.
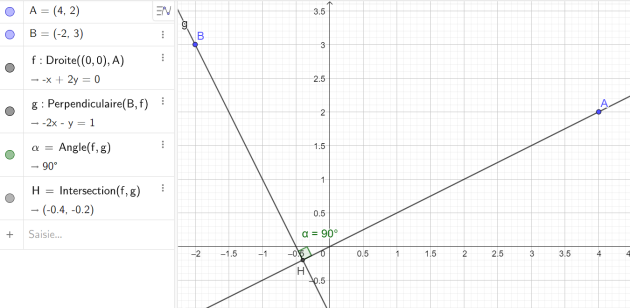
Soit A le point de coordonnées (4 ; 2).
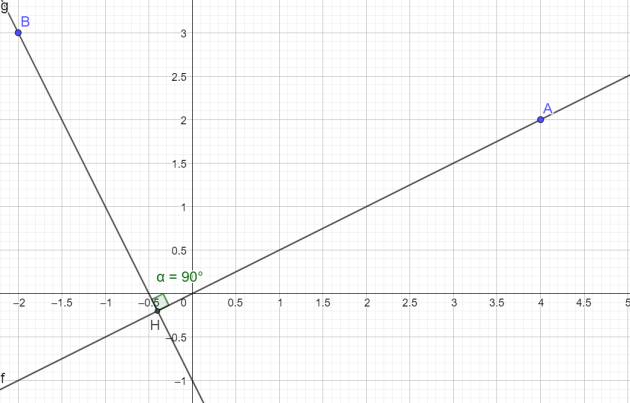
Soit H le projeté orthogonal du point B(–2 ; 3) sur la droite (OA),
Question
1.Faire une figure.
Question
2. En notant \((x_H ;y_H)\) les coordonnées du point H
et en utilisant que les vecteurs \(\vec{HB}\) et \(\vec{OA}\) sont orthogonaux
et donc que \(\vec{HB}.\vec{OA}=0\)
montrer que ces coordonnées vérifient :
\(y_H = – 2x_H – 1\)
Solution
\(\vec{HB}=\left( \begin{array}{c} x_B-x_H \\ y_B-y_H \end{array} \right)\)
\(\iff \vec{HB}=\left( \begin{array}{c} -2-x_H \\ 3-y_H \end{array} \right)\)
\(\vec{OA}=\left( \begin{array}{c} x_A-x_O \\ y_A-y_O \end{array} \right)\)
\(\iff \vec{OA}=\left( \begin{array}{c} 4-0 \\ 2-0\end{array} \right)\)
\(\iff \vec{OA}=\left( \begin{array}{c} 4 \\ 2 \end{array} \right)\)
\(\vec{HB}.\vec{OA}=\left( \begin{array}{c} -2-x_H \\ 3-y_H \end{array} \right).\left( \begin{array}{c} 4 \\ 2\end{array} \right)=0\)
\(\iff \vec{HB}.\vec{OA}=(-2-x_H) \times 4 + (3-y_H) \times 2=0\)
\(\iff \vec{HB}.\vec{OA}=-8-4x_H+ 6-2y_H=0\)
\(\iff -2-4x_H-2y_H=0\)
\(\iff -2y_H=4x_H+2\)
\(\iff y_H=-2x_H-1\)
Question
3.En traduisant que le point H appartient à la droite (OA)
montrer que ces coordonnées vérifient :
\(y_H = 0,5x_H\)
Solution
La droite (OA) est la représentation graphique d'une fonction linéaire,
elle est donc de la forme :
\(y=ax\)
Calcul du coefficient directeur :
\(a=\frac{y_A-y_O}{x_A-x_O}\)
\(\iff a=\frac{2-0}{4-0}=\frac{2}{4}=0,5\)
L'équation de la droite linéaire est donc \(y=0,5x\)
Comme le point \(H \in (OA)\),
les coordonnées du point H vérifient l'équation de la droite (OA) :
\(y_H=0,5x_H\)
Question
4.Résoudre le système :
\(\begin{cases}y= – 2x – 1\\y = 0,5x\end{cases}\)
En déduire les coordonnées du point H.
Vérifier ces coordonnées sur votre dessin.
Solution
\(\begin{cases}y= – 2x – 1\\y = 0,5x\end{cases}\)
\(– 2x – 1=0,5x\)
\(\iff – 2x=0,5x+1\)
\(\iff – 2x-0,5x=1\)
\(\iff – 2,5x=1\)
\(\iff x=\frac{1}{-2,5}\)
\(\iff x=\frac{-1}{2,5}\)
\(\iff x=\frac{-4}{10}=-0,4\)
\(\begin{cases}y= – 2 \times (-0,4)– 1\\y = 0,5 \times (-0,4)\end{cases}\)
\(\iff \begin{cases}y= 0,8– 1\\y = -0,2\end{cases}\)
\(\iff \begin{cases}y= – 0,2\\y = -0,2\end{cases}\)
Les coordonnées du point H sont donc (-0,4 ;-0,2)
Exercice 4
Soit \((O ;\vec{i} ;\vec{j})\) un repère orthonormé.
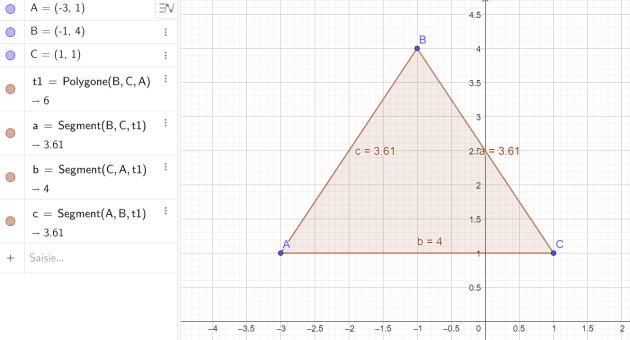
Soient les points A(–3 ;1), B(–1 ;4) et C(1 ;1).
Question
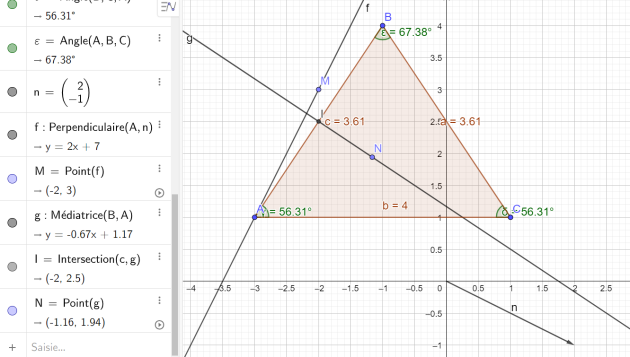
1.Faire une figure
Question
2.Montrer que le triangle ABC est isocèle.
Justifier que le triangle n'est ni équilatéral, ni rectangle.
Solution
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(\iff AB=\sqrt{(-1-(-3))^2+(4-1)^2}\)
\(\iff AB=\sqrt{(-1+3)^2+3^2}\)
\(\iff AB=\sqrt{2^2+3^2}\)
\(\iff AB=\sqrt{4+9}=\sqrt{13}\)
\(AC=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}\)
\(\iff AC=\sqrt{(1-(-3))^2+(1-1)^2}\)
\(\iff AC=\sqrt{(1+3)^2+0^2}\)
\(\iff AC=\sqrt{4^2}=4\)
\(BC=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}\)
\(\iff BC=\sqrt{(1-(-1))^2+(1-4)^2}\)
\(\iff BC=\sqrt{(1+1)^2+(-3)^2}\)
\(\iff BC=\sqrt{2^2+3^2}\)
\(\iff BC=\sqrt{4+9}=\sqrt{13}\)
Le triangle ABC a deux côtés de même longueur (AB=BC) donc le triangle est isocèle en B.
Le troisième côté [AC] est de longueur différente
donc le triangle ABC n'est pas équilatéral.
Le côté le plus long est AC :
\(AC^2=4^2=16\)
et \(AB^2+BC^2=\sqrt{13}^2+\sqrt{13}^2=13+13=26\)
donc l'égalité du théorème de Pythagore n'est pas vérifiée,
on en déduit que le triangle ABC n'est pas rectangle.
Question
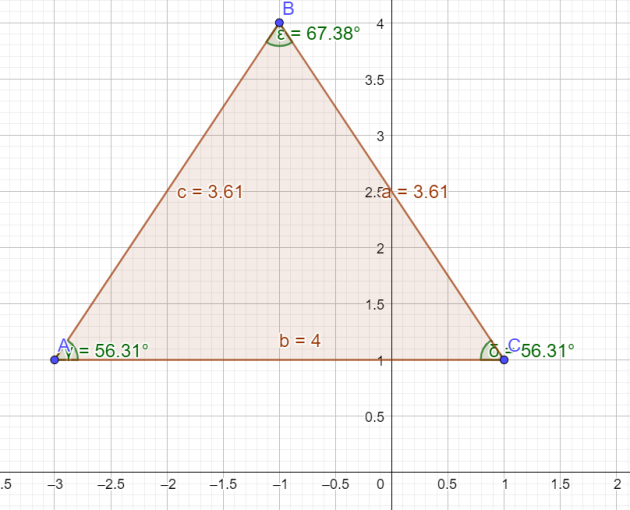
2.Calculer une valeur approchée à 0,01° près de chacun des angles du triangle.
Indice
Utiliser les formules d'Al-Kashi
Solution
Formules d'Al-Kashi :
\(\begin{cases}AB^2=AC^2+CB^2-2 AC \times CB \times cos(\widehat{ACB})\\AC^2=AB^2+CB^2-2 AB \times CB \times cos(\widehat{ABC})\\BC^2=BA^2+AC^2-2 BA \times AC \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}\sqrt{13}^2=4^2+\sqrt{13}^2-2 \times 4 \times \sqrt{13} \times cos(\widehat{ACB})\\4^2=\sqrt{13}^2+\sqrt{13}^2-2 \times \sqrt{13} \times \sqrt{13} \times cos(\widehat{ABC})\\\sqrt{13}^2=\sqrt{13}^2+4^2-2 \sqrt{13} \times 4 \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}13=16+13-8\sqrt{13} \times cos(\widehat{ACB})\\16=13+13-2 \times 13 \times cos(\widehat{ABC})\\13=13+16-8 \times \sqrt{13} \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}13=29-8\sqrt{13} \times cos(\widehat{ACB})\\16=26-26 \times cos(\widehat{ABC})\\13=29-8\sqrt{13} \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}13-29=-8\sqrt{13}cos(\widehat{ACB})\\16-26=-26cos(\widehat{ABC})\\13-29=-8\sqrt{13} \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}-16=-8\sqrt{13}cos(\widehat{ACB})\\-10=-26cos(\widehat{ABC})\\-16=-8\sqrt{13} \times cos(\widehat{CAB})\end{cases}\)
\(\iff \begin{cases}cos(\widehat{ACB})=\frac{-16}{-8\sqrt{13}}\\cos(\widehat{ABC})=\frac{-10}{-26}\\cos(\widehat{CAB})=\frac{-16}{-8\sqrt{13}}\end{cases}\)
\(\iff \begin{cases}cos(\widehat{ACB})=\frac{2}{\sqrt{13}}\\cos(\widehat{ABC})=\frac{10}{26}\\cos(\widehat{CAB})=\frac{2}{\sqrt{13}}\end{cases}\)
\(\iff \begin{cases}cos(\widehat{ACB})=\frac{2\sqrt{13}}{\sqrt{13}^2}\\cos(\widehat{ABC})=\frac{5}{13}\\cos(\widehat{CAB})=\frac{2\sqrt{13}}{\sqrt{13}^2}\end{cases}\)
\(\iff \begin{cases}cos(\widehat{ACB})=\frac{2\sqrt{13}}{13}\\cos(\widehat{ABC})=\frac{5}{13}\\cos(\widehat{CAB})=\frac{2\sqrt{13}}{13}\end{cases}\)
\(\iff \begin{cases}\widehat{ACB}=Arccos(\frac{2\sqrt{13}}){13}\\\widehat{ABC})=Arccos(\frac{5}{13})\\\widehat{CAB}=Arccos(\frac{2\sqrt{13}}{13})\end{cases}\)
\(\iff \begin{cases}\widehat{ACB}=Arccos(\frac{2\sqrt{13}}{13})\simeq 56,3°\\\widehat{ABC})=Arccos(\frac{5}{13})\simeq 67,4°\\\widehat{CAB}=Arccos(\frac{2\sqrt{13}}{13})\simeq 56,3\end{cases}\)
Question
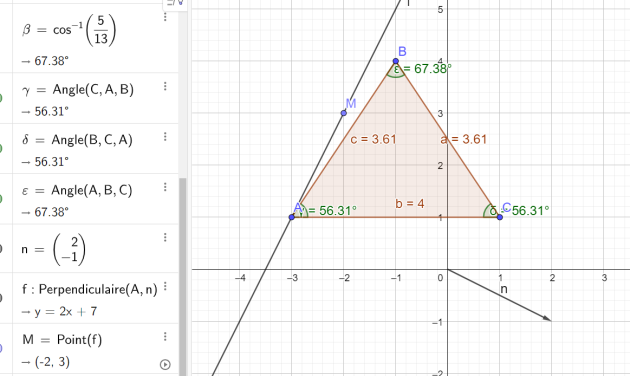
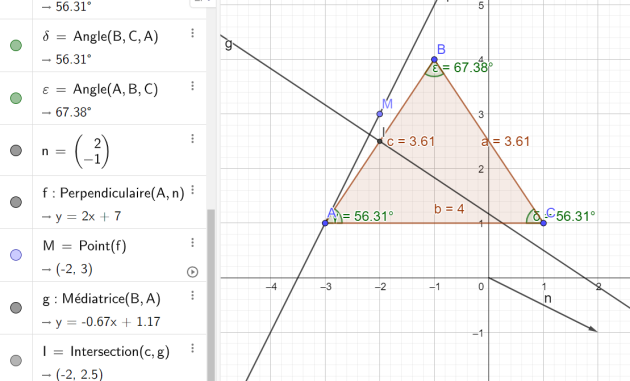
3. Quelle est l'équation réduite de la droite passant par la point A et de vecteur normal \(\vec{n}(2 ; –1)\) ?
Solution
Soit M un point de la droite passant par la point A et de vecteur normal \(\vec{n}(2 ; –1)\) de coordonnées \((x ;y)\)
alors
\(\vec{AM}=\left( \begin{array}{c} x_M-x_A \\ y_M-y_A \end{array} \right)\)
\(\iff \vec{AM}=\left( \begin{array}{c} x-(-3) \\ y-1 \end{array} \right)\)
\(\iff \vec{AM}=\left( \begin{array}{c} x+3 \\ y-1 \end{array} \right)\)
\(\vec{AM}.\vec{n}=\left( \begin{array}{c} x+3 \\ y-1 \end{array} \right).\left( \begin{array}{c} 2 \\ -1 \end{array} \right)=0\)
\(\iff \vec{AM}.\vec{n}=2(x+3) -1( y-1)=0\)
\(\iff 2x+6 - y+1=0\)
\(\iff 2x- y+7=0\)
\(\iff - y=-2x-7\)
\(\iff y=2x+7\)
L'équation réduite de la droite passant par la point A et de vecteur normal \(\vec{n}(2 ; –1)\) est \(y=2x+7\)
Question
4. Donner une équation de la médiatrice du segment [AB]
Solution
Equation de la médiatrice de [AB] :
Soit I le milieu de [AB] :
\(\begin{cases}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{-3+(-1)}{2}\\y_I=\frac{1+4}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{-4}{2}\\y_I=\frac{5}{2}\end{cases}\)
\(\iff \begin{cases}x_I=-2\\y_I=2,5\end{cases}\)
Soit N un point de la médiatrice du segment [AB]
alors les vecteurs \(\vec{AB}\) et \(\vec{IN}\) sont orthogonaux donc
\(\vec{AB}.\vec{IN}=0\)
\(\vec{AB}=\left( \begin{array}{c} x_B-x_A \\ y_B-y_A \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} -1-(-3) \\ 4-1 \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} -1+3 \\ 3 \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)\)
\(\vec{AB}=\left( \begin{array}{c} x_B-x_A \\ y_B-y_A \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} -1-(-3) \\ 4-1 \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} -1+3 \\ 3 \end{array} \right)\)
\(\iff \vec{AB}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right)\)
\(\vec{IN}=\left( \begin{array}{c} x_N-x_I \\ y_N-y_I \end{array} \right)\)
\(\iff \vec{IN}=\left( \begin{array}{c} x-(-2) \\ y-2,5 \end{array} \right)\)
\(\iff \vec{IN}=\left( \begin{array}{c} x+2 \\ y-2,5 \end{array} \right)\)
\(\vec{AB}.\vec{IN}=\left( \begin{array}{c} 2 \\ 3 \end{array} \right).\left( \begin{array}{c} x+2 \\ y-2,5 \end{array} \right)=0\)
\(\vec{AB}.\vec{IN}=2(x+2)+3(y-2,5)=0\)
\(\iff \vec{AB}.\vec{IN}=2x+4+3y-7,5=0\)
\(\iff 2x+3y-3,5=0\)
\(\iff 3y=-2x+3,5\)
\(\iff y=-\frac{2}{3}x+\frac{3,5}{3}\)
\(\iff y=-\frac{2}{3}x+\frac{7}{6}\)
Exercice 5
Soit \((O ;\vec{i} ;\vec{j})\) un repère orthonormé.
Donner une équation des cercles :
Question
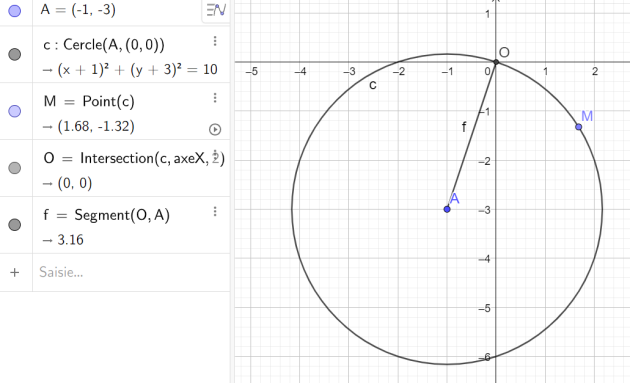
de centre (–1 ; –3) passant par l'origine ;
Solution
Soit M un point du cercle de centre (–1 ; –3) passant par l'origine du repère
de coordonnées \((x ;y)\)
alors
AM=OA
\(\begin{cases}AM=\sqrt{(x_M-x_A)^2+(y_M-y_A)^2}\\OA=\sqrt{(x_A-x_O)^2+(y_A-y_O)^2}\end{cases}\)
\(\begin{cases}AM=\sqrt{(x-(-1))^2+(y-(-3))^2}\\OA=\sqrt{(-1-0)^2+(-3-0)^2}\end{cases}\)
\(\iff \begin{cases}AM=\sqrt{(x+1)^2+(y+3)^2}\\OA=\sqrt{(-1)^2+(-3)^2}\end{cases}\)
\(\iff \begin{cases}AM=\sqrt{(x+1)^2+(y+3)^2}\\OA=\sqrt{1+9}\end{cases}\)
\(\iff \begin{cases}AM=\sqrt{(x+1)^2+(y+3)^2}\\OA=\sqrt{10}\end{cases}\)
AM=OA
\(\iff AM^2=OA^2\)
\(\iff \sqrt{(x+1)^2+(y+3)^2}^2=\sqrt{10}^2\)
\(\iff (x+1)^2+(y+3)^2=10\)
Question
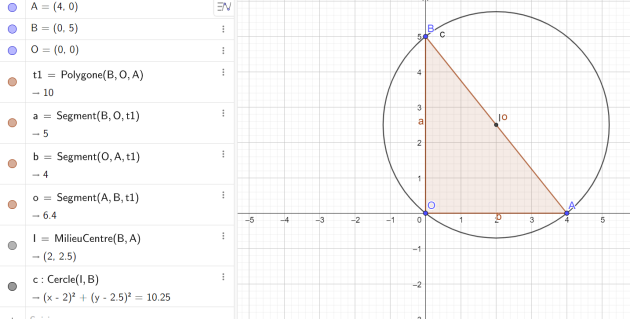
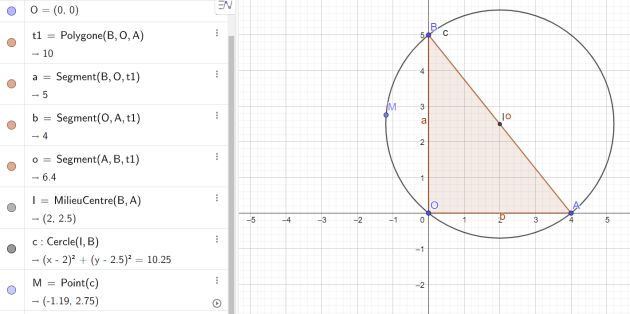
circonscrit au triangle OAB, où A et B ont pour coordonnées respectivement (4 ; 0) et (0 ; 5).
Solution
Montrons que le triangle OAB est rectangle en O
\(OA=\sqrt{(x_A-x_O)^2+(y_A-y_O)^2}\)
\(\iff OA=\sqrt{(4-0)^2+(0-0)^2}\)
\(\iff OA=\sqrt{4^2+0^2}\)
\(\iff OA=\sqrt{16+0}\)
\(\iff OA=\sqrt{16}=4\)
\(OB=\sqrt{(x_B-x_O)^2+(y_B-y_O)^2}\)
\(\iff OB=\sqrt{(0-0)^2+(5-0)^2}\)
\(\iff OB=\sqrt{0^2+5^2}\)
\(\iff OB=\sqrt{0+25}\)
\(\iff OB=\sqrt{25}=5\)
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(\iff AB=\sqrt{(0-4)^2+(5-0)^2}\)
\(\iff AB=\sqrt{4^2+5^2}\)
\(\iff AB=\sqrt{16+25}\)
\(\iff AB=\sqrt{41}\)
Le côté le plus long est AB :
\(AB^2=\sqrt{41}^2=41\)
et \(OA^2+OB^2=4^2+5^2=16+25=41\)
donc l'égalité du théorème de Pythagore est vérifiée,
on en déduit que le triangle OAB est rectangle en O d'hypoténuse [AB].
\(\color{red}{\text{Propriété :}}\)
\(\color{red}{\text{Un tiangle rectangle est inscrit dans un demi cercle de diamètre le milieu de son hypoténuse.}}\)
L'hypoténuse du triangle OAB est [AB] de milieu I tel que :
\(\begin{cases}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{4+0}{2}\\y_I=\frac{0+5}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{4}{2}\\y_I=\frac{5}{2}\end{cases}\)
\(\iff \begin{cases}x_I=2\\y_I=2,5\end{cases}\)
Soit M un point du cercle circonscrit au triangle OAB
de coordonnées \((x ;y)\)
alors
\(IA=IM\)
\(\begin{cases}IA=\sqrt{(x_A-x_I)^2+(y_A-y_I)^2}\\IM=\sqrt{(x_M-x_I)^2+(y_M-y_I)^2}\end{cases}\)
\(\begin{cases}IA=\sqrt{(4-2)^2+(0-2,5)^2}\\IM=\sqrt{(x-2)^2+(y-2,5)^2}\end{cases}\)
\(\iff \begin{cases}IA=\sqrt{2^2+(-2,5)^2}\\IM=\sqrt{(x-2)^2+(y-2,5)^2}\end{cases}\)
\(\iff \begin{cases}IA=\sqrt{4+6,25}\\IM=\sqrt{(x-2)^2+(y-2,5)^2}\end{cases}\)
\(\iff \begin{cases}IA=\sqrt{10,25}\\IM=\sqrt{(x-2)^2+(y-2,5)^2}\end{cases}\)
\(IA=IM\)
\(\iff IA^2=IM^2\)
\(\iff \sqrt{10,25}^2=\sqrt{(x-2)^2+(y-2,5)^2}^2\)
\(\iff 10,25=(x-2)^2+(y-2,5)^2\)
\(\iff (x-2)^2+(y-2,5)^2=10,25\)