Exercice : DS 2025 A : Produit Scalaire

Exercice 1

Soit ABC un parallélogramme tel que AB=4 ;AC=5 et \(\widehat{BAC}=\frac{\pi}{3}\)

La figure n'est pas à l'échelle.

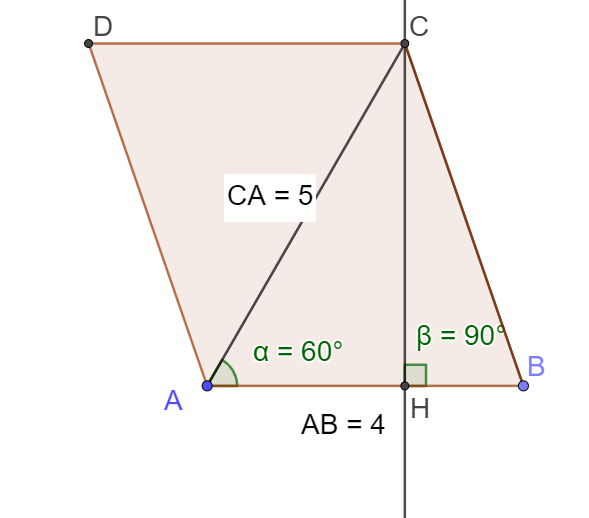
Question

  1. Déterminer le produit scalaire \(\vec{AB}.\vec{AC}\)

Solution

\(\overrightarrow{AB} \cdot \overrightarrow{AC} = ||\vec{AB}|| \times ||\vec{AC}|| \times \cos\left( (\vec{AB};\vec{AC})\right)\)

\(\Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} = AB \times AC \times \cos\left(\frac{\pi}{3}\right) = 4 \times 5 \times \frac{1}{2} = 10\)

Question

2.En utilisant la formule donnant le produit scalaire \(\vec{AB}.\vec{AC}\)

en fonction de la norme du projeté du vecteur \(\vec{AC}\) sur le vecteur \(\vec{AB}\),

déterminer la longueur AH

Solution

Le projeté orthogonal du vecteur \(\vec{AC}\) sur la droite  \((AB)\) est le vecteur \(\vec{AH}\)

\(\overrightarrow{AB} \cdot \overrightarrow{AC} = AB \times AH= 10\)

\(\iff AH=\frac{10}{4}=2,5\)

Exercice 2

On considère la figure suivante :

La figure n'est pas à l'échelle.

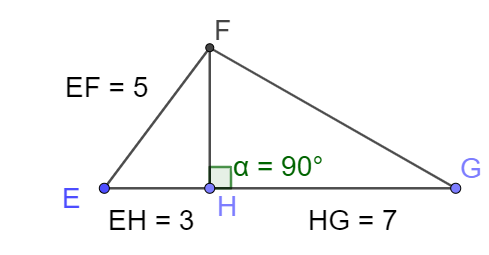
Question

  1. Déterminer le produit scalaire \(\vec{EF}.\vec{EG}\)

Solution

Le projeté orthogonal du vecteur \(\vec{EF}\) sur la droite  \((EG)\) est le vecteur \(\vec{EH}\)

\(\overrightarrow{EF} \cdot \overrightarrow{EG} = EH \times EG = 3 \times 10=30\)

Question

2. En déduire la mesure de l'angle de vecteurs \((\vec{EF};\vec{EG})\) arrondi au degré près.

Solution

\(\overrightarrow{EF} \cdot \overrightarrow{EG} = ||\vec{EF}|| \times ||\vec{EG}|| \times \cos\left( (\vec{EF};\vec{EG})\right)\)

\(\Rightarrow ||\vec{EF}|| \times ||\vec{EG}|| \times \cos\left( (\vec{EF};\vec{EG})\right)=30\)

\(\iff 5 \times 10 \times \cos\left( (\vec{EF};\vec{EG})\right)=30\)

\(\iff 50 \times \cos\left( (\vec{EF};\vec{EG})\right)=30\)

\(\iff \cos\left( (\vec{EF};\vec{EG})\right)=\frac{30}{50}\)

\(\iff \cos\left( (\vec{EF};\vec{EG})\right)=\frac{3}{5}\)

\(\iff \cos\left( (\vec{EF};\vec{EG})\right)=0,6\)

\(\iff (\vec{EF};\vec{EG})=-Arccos(0,6) \simeq -53°\)

En effet l'angle de vecteurs \((\vec{EF};\vec{EG})\) est orienté dans le sens opposé du sens positif du cercle trigonométrique.

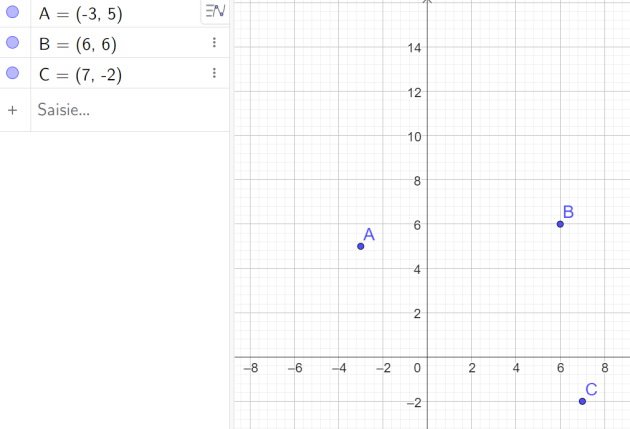
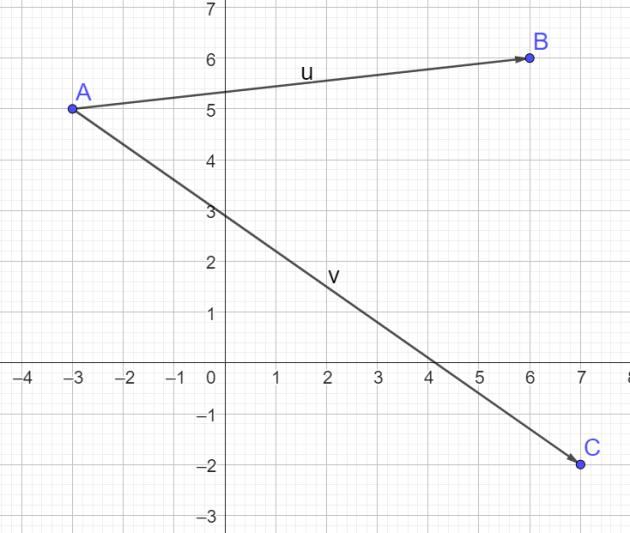
Exercice 3

Le plan est rapporté à un repère orthonormé.

On considère les points de coordonnées :

A(-3 ;5) ; B(6 ;6) ; C(7 ;-2)

Question

  1. Déterminer le produit scalaire \(\vec{AB}.\vec{AC}\)

Solution

  • \(\vec{AB}=\left( \begin{array}{c}x_B−x_A\\y_B−y_A\end{array} \right)\)\(\)

    \(\Rightarrow \vec{AB}=\left( \begin{array}{c}6−(−3)\\6−5\end{array} \right)\)\(\)

    \(\iff \vec{AB}=\left( \begin{array}{c}9\\1\end{array} \right)\)

  • \(\vec{AC}=\left( \begin{array}{c}x_C−x_A\\y_C−y_A\end{array} \right)\)\(\)

    \(\Rightarrow \vec{AC}=\left( \begin{array}{c}7−(−3)\\-2−5\end{array} \right)\)\(\)

    \(\iff \vec{AC}=\left( \begin{array}{c}10\\-7\end{array} \right)\)\(\)

  • \(\vec{AB} \cdot \vec{AC}=9×10+1×(−7)=83\)

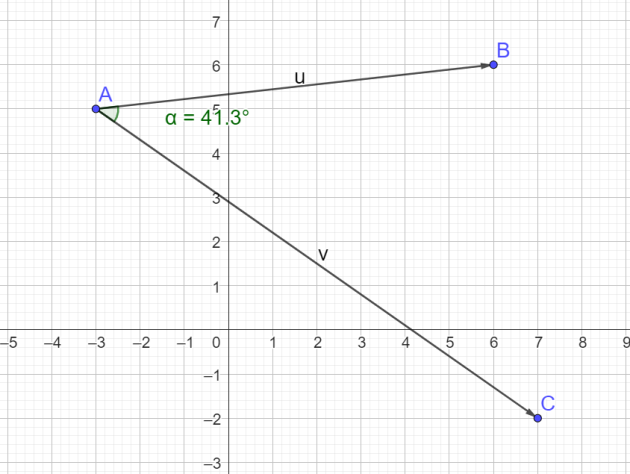
Question

2. En déduire la mesure de l'angle de vecteurs \((\vec{AB};\vec{AC})\) arrondie au dixième.

Solution

\(\overrightarrow{AB} \cdot \overrightarrow{AC} = ||\vec{AB}|| \times ||\vec{AC}|| \times \cos\left( (\vec{AB};\vec{AC})\right)\)

  • Calcul des normes des vecteurs :

\(||\vec{AB}||=\sqrt{9^2+1^2​}=\sqrt{81+1}=\sqrt{82}\)​

\(||\vec{AC}||=\sqrt{10^2+(-7)^2​}=\sqrt{100+49}=\sqrt{149}\)​

\(\Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} = \sqrt{82}​ \times\sqrt{149} \times \cos\left( (\vec{AB};\vec{AC})\right)=83\)

\(\iff \sqrt{82}​ \times\sqrt{149} \times \cos\left( (\vec{AB};\vec{AC})\right)=83\)

\(\iff \cos\left( (\vec{AB};\vec{AC})\right)=\frac{83}{\sqrt{82}​ \times\sqrt{149 }}\)

\(\iff (\vec{AB};\vec{AC})=-Arccos(\frac{83}{\sqrt{82}​ \times\sqrt{149 }})\simeq -41°\)

En effet l'angle de vecteurs \((\vec{AB};\vec{AC})\) est orienté dans le sens opposé du sens positif du cercle trigonométrique.

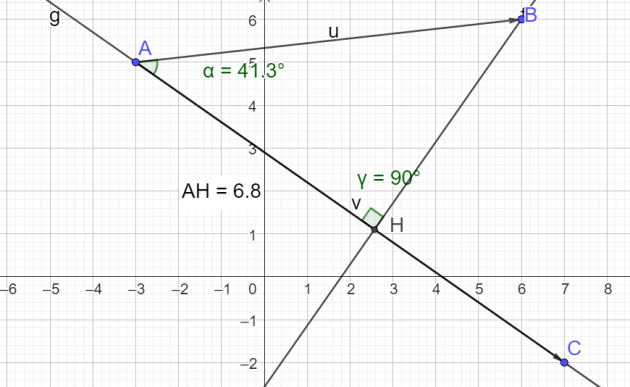
Question

3. Soit H le projeté orthogonal du point B sur la droite (AC), déterminer la longueur AH

Solution

Le projeté orthogonal du vecteur \(\vec{AB}\) sur la droite  \((AC)\) est le vecteur \(\vec{AH}\)

\(\overrightarrow{AB} \cdot \overrightarrow{AC} = AH \times AC= 83\)

\(\Rightarrow AH \times \sqrt{149}= 83\)

\(\iff AH = \frac{83}{\sqrt{149}}\)

\(\Rightarrow AH = \simeq 6,8\)

Exercice 4

Le plan est rapporté à un repère orthonormé.

On considère les points de coordonnées :

A(-1 ;0) ; B(-2 ;-7) ; C(12 ;-9) ; D(-9 ;-6)

Question

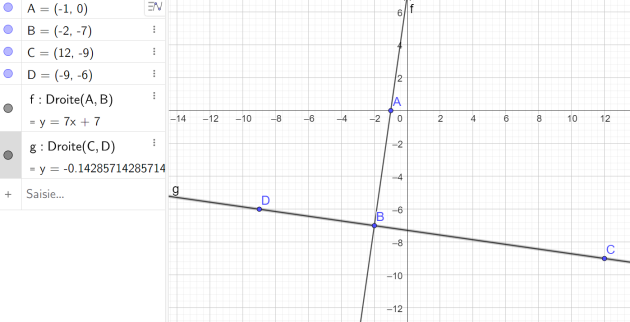
Démontrer que les droites (AB) et (CD) sont perpendiculaires.

Solution

  • \(\vec{AB}=\left( \begin{array}{c}x_B−x_A\\y_B−y_A\end{array} \right)\)\(\)

    \(\Rightarrow \vec{AB}=\left( \begin{array}{c}-2−(−1)\\-7−0\end{array} \right)\)\(\)

    \(\vec{AB}=\left( \begin{array}{c}-2+1\\-7−0\end{array} \right)\)\(\)

    \(\iff \vec{AB}=\left( \begin{array}{c}-1\\-7\end{array} \right)\)

  • \(\vec{CD}=\left( \begin{array}{c}x_D−x_C\\y_D−y_C\end{array} \right)\)\(\)

    \(\Rightarrow \vec{CD}=\left( \begin{array}{c}-9−12\\-6−(-9)\end{array} \right)\)\(\)

    \(\Rightarrow \vec{CD}=\left( \begin{array}{c}-21\\-6+9\end{array} \right)\)\(\)

    \(\Rightarrow \vec{CD}=\left( \begin{array}{c}-21\\3\end{array} \right)\)

  • \(\overrightarrow{AB} \cdot \overrightarrow{CD} =(−1)×(−21)+(−7)×3=21−21=0\)

Le produit scalaire des vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) est nul donc les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont orthogonaux.

Les droites (AB) et (CD) sont donc perpendiculaires.

Exercice 5

On considère la figure ci-contre avec le quadrilatère OABC qui est un carré.

D le milieu du segment [OC]

Question

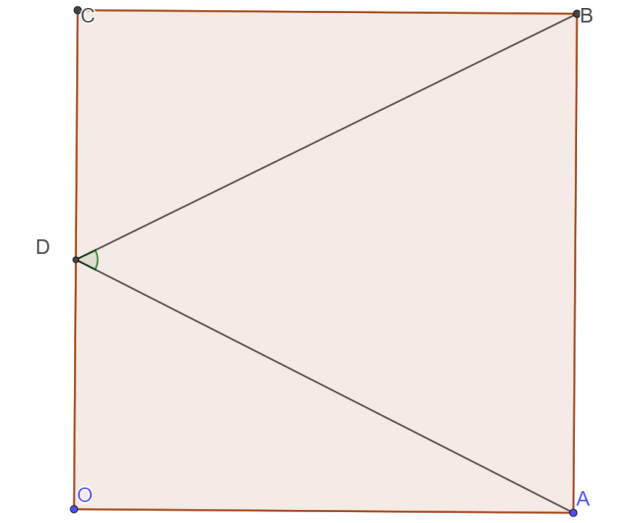
  1. Donner les coordonnées des points O,A,B,C,D dans le repère orthonormé (\(O ;\vec{OA},\vec{OC}\)).

Question

2. Donner les coordonnées des vecteurs \(\vec{DA}\) et \(\vec{DB}\) dans le repère orthonormé (\(O ;\vec{OA},\vec{OC}\)).

Solution

  • \(\vec{DA}=\left( \begin{array}{c}x_A−x_D\\y_A−y_D\end{array} \right)\)\(\)

    \(\Rightarrow \vec{DA}=\left( \begin{array}{c}1−0\\0−\frac{1}{2}\end{array} \right)\)\(\)

    \(\iff \vec{DA}=\left( \begin{array}{c}1\\−\frac{1}{2}\end{array} \right)\)\(\)

  • \(\vec{DB}=\left( \begin{array}{c}x_B−x_D\\y_B−y_D\end{array} \right)\)\(\)

    \(\Rightarrow \vec{DB}=\left( \begin{array}{c}1−0\\1−\frac{1}{2}\end{array} \right)\)\(\)

    \(\iff \vec{DB}=\left( \begin{array}{c}1\\\frac{1}{2}\end{array} \right)\)\(\)

Question

3.Calculer le produit scalaire \(\vec{DA}.\vec{DB}\)

Solution

\(\overrightarrow{DA} \cdot \overrightarrow{DB} =1×1+(−\frac{1}{2})×\frac{1}{2}=1−\frac{1}{4}=\frac{3}{4}\)

Question

4. Calculer les normes des vecteurs \(\vec{DA}\) et \(\vec{DB}\) dans le repère orthonormé (\(O ;\vec{OA},\vec{OB}\)) grâce au théorème de Pythagore.

Solution

  • Dans le triangle DAO rectangle en O, d'hypoténuse [DA] :

\(DA^2=DO^2+OA^2\)

\(\iff ||\vec{DA}|| =\sqrt{1^2+(−0,5)^2​}=\sqrt{1+0,25​}=\sqrt{1,25​}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}\)

  • Dans le triangle DCB rectangle en B, d'hypoténuse [DB] :

\(DB^2=DC^2+CB^2\)

\(||\vec{DB}|| =\sqrt{1^2+0,5^2​}=\sqrt{1+0,25​}=\sqrt{1,25​}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}\)

Question

5.En utilisant la question 4. et le produit scalaire \(\vec{DA}.\vec{DB}\),

déterminer la mesure de l'angle de vecteurs \((\vec{DA} ;\vec{DB})\)

Solution

\(\overrightarrow{DA} \cdot \overrightarrow{DB} = ||\vec{DA}|| \times ||\vec{DB}|| \times \cos\left( (\vec{DA};\vec{DB})\right)\)

\(\Rightarrow \overrightarrow{DA} \cdot \overrightarrow{DB} = \frac{\sqrt{5}}{2}​ \times \frac{\sqrt{5}}{2} \times \cos\left( (\vec{DA};\vec{DB})\right)=\frac{3}{4}\)

\(\iff \frac{(\sqrt{5})^2}{4}\times \cos\left( (\vec{DA};\vec{DB})\right)=\frac{3}{4}\)

\(\iff \frac{5}{4}\times \cos\left( (\vec{DA};\vec{DB})\right)=\frac{3}{4}\)

\(\iff \cos\left( (\vec{DA};\vec{DB})\right)=\frac{\frac{3}{4}}{\frac{5}{4}}\)

\(\iff \cos\left( (\vec{DA};\vec{DB})\right)=\frac{3}{4} \times \frac{4}{5}\)

\(\iff \cos\left( (\vec{DA};\vec{DB})\right)=\frac{3}{5}\)

\(\iff (\vec{DA};\vec{DB})=Arccos(0,6) \simeq 53°\)

En effet l'angle de vecteurs \((\vec{DA};\vec{DB})\) est orienté dans le sens positif du cercle trigonométrique.