Exercice : Puissance d'un point par rapport à un cercle
(C) est un cercle, $M un point du plan
et d une droite passant par M.
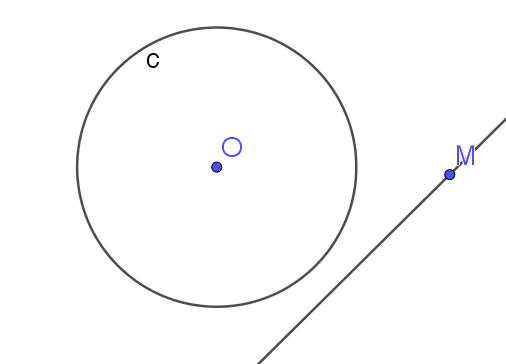
On se propose d'étudier le produit scalaire
\(\vec{MA} .\vec{MB}\)
où A et B sont les points d'intersection,
lorsqu'ils existent, de la droite d et du cercle (C).
Lancer le logiciel Geogebra.
\(\color{magenta}{\text{I/Construction:}}\)
A partir d'une figure vide:
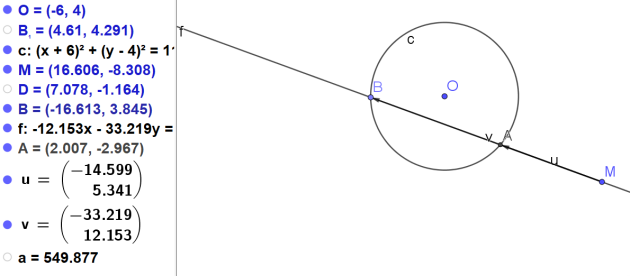
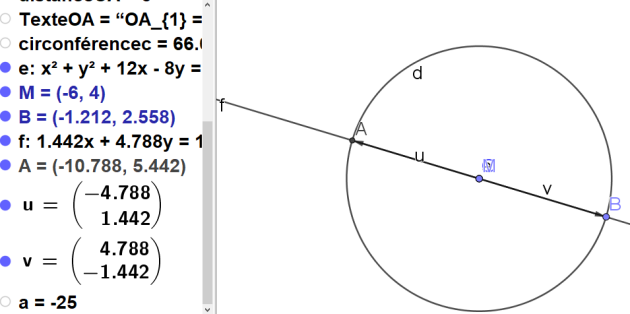
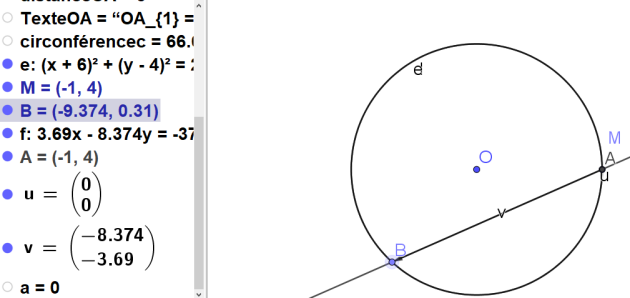
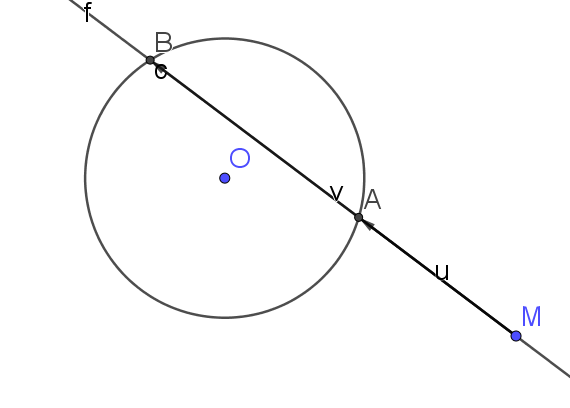
a.Placer un point O.
b. Dessiner le cercle C de centre O et de rayon 5
c. Placer un point M.
d. Dessiner une droite d passant par M.
e. Déplacer le point de la droite d différent de M afin que la droite coupe le cercle en deux points.
f. Placer les points d'intersection A et B de la droite d et du cercle C.
g.Dessiner des représentants des vecteurs \(\vec{MA}\) et \(\vec{MB}\)
Le vecteur \(\vec{MA}\) est enregistré sous le nom \(\vec{u}\) et le vecteur \(\vec{MB}\) sous le nom \(\vec{v}\).
h.Dans la zone de saisie, rentrer:
Ceci va définir le produit scalaire \(\vec{MA} .\vec{MB}\)
Pour connaître la valeur du produit scalaire: lire la valeur dans la fenêtre algèbre du logiciel
Question
\(\color{red}{\text{Conjectures graphiques:}}\)
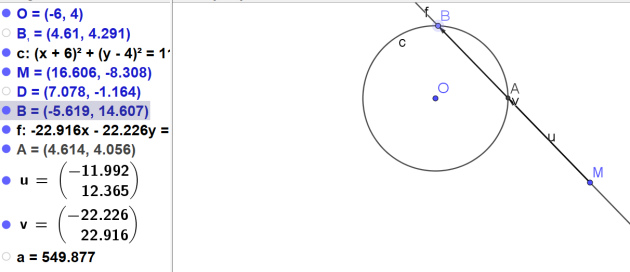
1. Faire varier la position de la droite d
sans faire varier la position du point M.
Que constate t-on?
Solution
Le produit scalaire \(\vec{MA}.\vec{MB}\) reste constant si on déplace la droite (d)
Question
2. Faire bouger le point M afin d'étudier le signe de \(\vec{MA} .\vec{MB}\)
Solution
Si le point M est à l'extérieur du cercle,
le produit scalaire \(\vec{MA}.\vec{MB}\) est positif.
Si le point M est sur le cercle,
le produit scalaire \(\vec{MA}.\vec{MB}\) est nul.
Si le point M est à l'intérieur du cercle,
le produit scalaire \(\vec{MA}.\vec{MB}\) est négatif.
Question
\(\color{red}{\text{II/Démonstration des résultats:}}\)
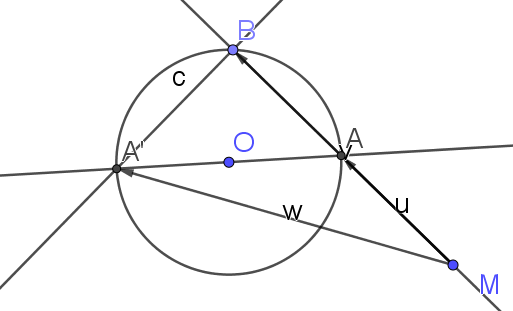
Placer le point A' diamétralement opposé à A sur le cercle C.
Question
1.Montrer que \(\vec{MA} .\vec{MB}=\vec{MA} .\vec{MA'}\)
Solution
\(\vec{MA} .\vec{MB}=\vec{MA} .\vec{MA'}\)
car B se projette orthogonalement en A' sur (AB)
Question
2.En utilisant le fait que
\(\vec{MA}=\vec{MO}+\vec{OA}\)
et \(\vec{MA'} =\vec{MO}+\vec{OA'}\)
calculer \(\vec{MA} .\vec{MB}\)
et en déduire qu'il ne dépend que de M et du cercle C.
Solution
\(\vec{MA} .\vec{MB}\)
\(=\vec{MA} .\vec{MA'}\)
\(=(\vec{MO}+\vec{OA})(\vec{MO}+\vec{OA'})\)
\(=\vec{MO}.\vec{MO}+\vec{MO}.\vec{OA'}+\vec{OA}.\vec{MO}+\vec{OA}.\vec{OA'}\)
\(=MO^2+\vec{MO}.(\vec{OA'}+\vec{OA})+\vec{OA}.\vec{OA'}\)
or \(\vec{OA'}=-\vec{OA}\)
donc
\(\vec{MA} .\vec{MB}=MO^2+\vec{MO}.(-\vec{OA}+\vec{OA})+\vec{OA}.(-\vec{OA})\)
\(\iff \vec{MA} .\vec{MB}=MO^2-OA^2\)
\(\iff \vec{MA} .\vec{MB}=OM^2-R^2\)
\(\iff \vec{MA} .\vec{MB}=OM^2-5^2\)
\(\iff \vec{MA} .\vec{MB}=OM^2-25\)
Le produit scalaire \(\vec{MA} .\vec{MB}\)
ne dépend que de la distance OM
et ne dépend pas de la droite (d).
Question
3.Utiliser l'expression de \(\vec{MA} .\vec{MB}\)
trouvée à la question précédente
pour étudier le signe de ce produit scalaire.
Solution
\(\vec{MA} .\vec{MB}=OM^2-R^2\)
Si le point M est à l'extérieur du cercle (OM>R),
le produit scalaire \(\vec{MA}.\vec{MB}\) est positif.
Si le point M est sur le cercle (OM=R),le produit scalaire \(\vec{MA}.\vec{MB}\) est nul.
Si le point M est à l'intérieur du cercle (OM<R),le produit scalaire \(\vec{MA}.\vec{MB}\) est négatif.
\(\color{red}{\text{III/ Prolongement:}}\)
On vient de démontrer que \(\vec{MA} .\vec{MB}\)
ne dépend pas de la position de la droite d.
Question
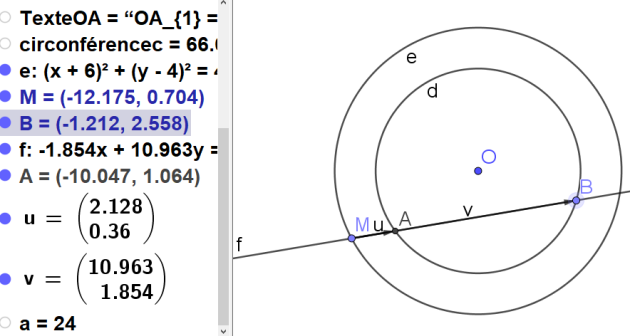
1.Déterminer l'ensemble des points M
tels que \(\vec{MA} .\vec{MB}\) soit égal à 24.
Solution
\(\vec{MA}.\vec{MB}=OM^2-25=24\)
\(\iff OM^2=49\)
\(\iff OM=7\)
L'ensemble des points M
tels que \(\vec{MA} .\vec{MB}\) soit égal à 24
est le cercle de centre O et de rayon 7
Question
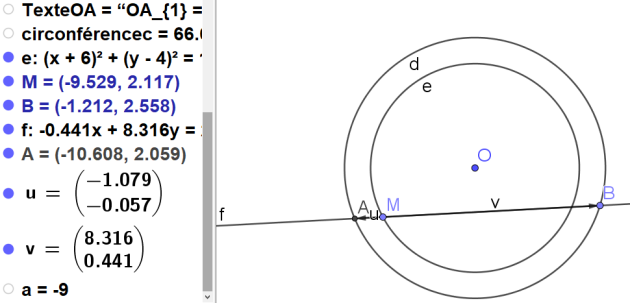
2.Déterminer l'ensemble des points M tels que \(\vec{MA} .\vec{MB}\) soit égal à -9.
Solution
\(\vec{MA}.\vec{MB}=OM^2-25=-9\)
\(\iff OM^2=16\)
\(\iff OM=4\)
L'ensemble des points M
tels que \(\vec{MA} .\vec{MB}\) soit égal à -9
est le cercle de centre O et de rayon 4
Question
3.Déterminer l'ensemble des points M tels que \(\vec{MA} .\vec{MB}\) soit égal à -25.
Solution
\(\vec{MA}.\vec{MB}=OM^2-25=-25\)
\(\iff OM^2=0\)
\(\iff OM=0\)
L'ensemble des points M
tels que \(\vec{MA} .\vec{MB}\) soit égal à -25
est le centre O du cercle.
Question
4.Déterminer l'ensemble des points M tels que \(\vec{MA} .\vec{MB}\) soit égal à 0.
Solution
\(\vec{MA}.\vec{MB}=OM^2-25=0\)
\(\iff OM^2=25\)
\(\iff OM=5\)
L'ensemble des points M
tels que \(\vec{MA} .\vec{MB}\) soit égal à 0
est le cercle centre O et de rayon 5
\(\color{red}{\text{B/ Axe radical de deux cercles (Eleves avancés)}}\)
\(\color{red}{\text{Définition :}}\)
\(\color{red}{\text{L'axe radical de deux cercles, de centres distincts,}}\)
\(\color{red}{\text{est l'ensemble des points ayant même puissance par rapport à ces deux cercles.}}\)
Question
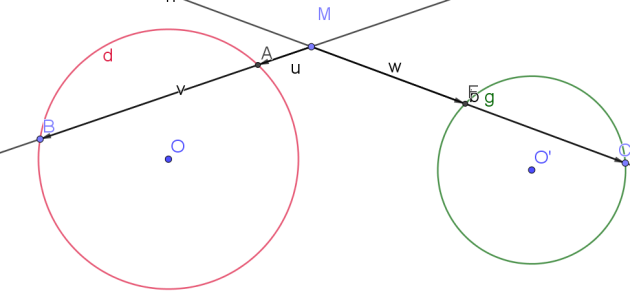
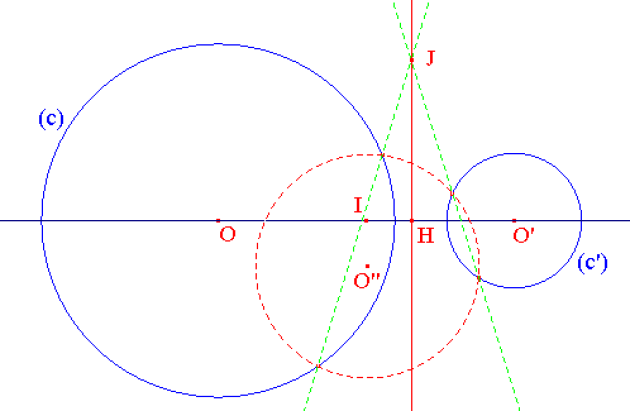
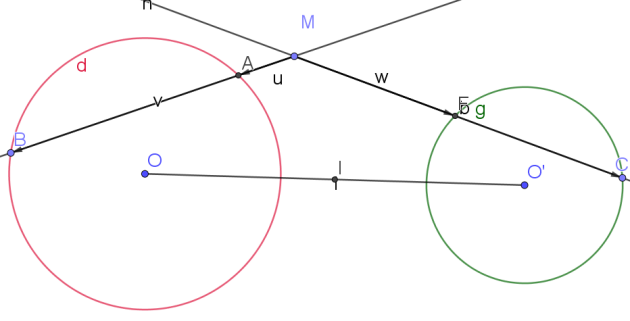
Soit deux cercles C(O, R) et C'(O', R') avec O et O' distincts.
1. Montrer que l'ensemble des points M de mêmes puissances par rapport aux deux cercles
vérifie : \(OM^2 - O'M^2 = R^2 - R'^2\)
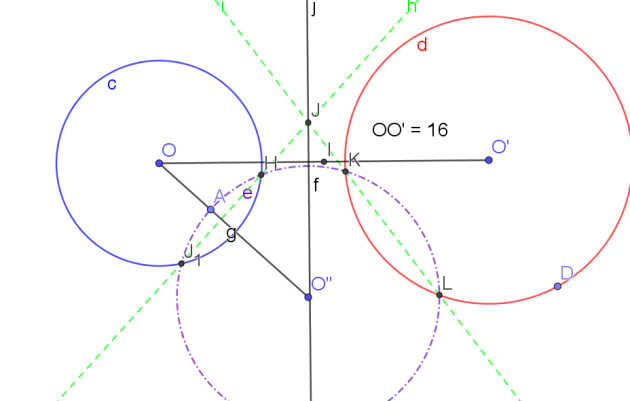
Le point J est appelé centre radical des 3 cercles ci-dessus. Ce centre n'existe que si O, O' et O" ne sont pas alignés.
Solution
\(\vec{MA} .\vec{MB}=OM^2-R^2\)
\(\vec{MA'} .\vec{MB'}=O'M^2-R'^2\)
or les puissances par rapport aux deux cercles sont égales
donc
\(\vec{MA} .\vec{MB}=\vec{MA'} .\vec{MB'}\)
\(\iff OM^2-R^2=O'M^2-R'^2\)
\(\iff OM^2 - O'M^2 = R^2 - R'^2\)
Question
2. En remarquant que
\(OM^2 - O'M^2 = ( \vec{OM}-\vec{O'M} ).(\vec{OM} + \vec{O'M})\).
Montrer en introduisant le point I milieu de [OO']
dans \(\vec{OM} + \vec{O'M}\)
que \(OM^2 - O'M^2= 2\vec{OO'}.\vec{IM}\)
Solution
\(OM^2 - O'M^2 = ( \vec{OM}-\vec{O'M} ).(\vec{OM} + \vec{O'M})\)
\(\iff OM^2 - O'M^2 = ( \vec{OM}+\vec{MO'} ).(\vec{OM} + \vec{O'M})\)
I milieu de [OO'] donc \(\vec{IO}=-\vec{IO'}\)
\(\iff OM^2 - O'M^2 = ( \vec{OM}+\vec{MO'} ).(\vec{OI}+\vec{IM} + \vec{O'I}+\vec{IM})\)
donc \(OM^2 - O'M^2 = ( \vec{OM}+\vec{MO'} ).(\vec{OI}+\vec{IM} + (-\vec{OI})+\vec{IM})\)
\(\iff OM^2 - O'M^2 = ( \vec{OM}+\vec{MO'} ).(2\vec{IM})\)
\(\iff OM^2 - O'M^2 = 2\vec{OO'}.\vec{IM}\)
Question
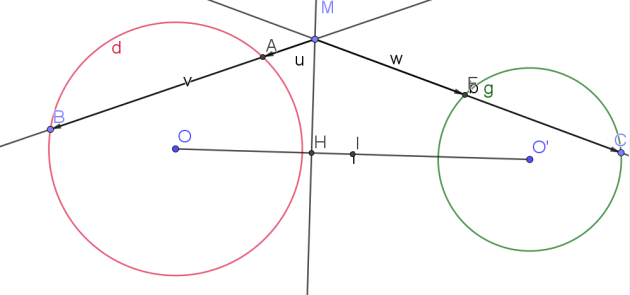
3. En notant H, le projeté du point M sur l'axe (OO'), montrer que :
\(2\vec{OO'} \times \vec{IH}=R^2-R'^2\)
Solution
\(OM^2 - O'M^2 = 2\vec{OO'}.\vec{IM}=2\vec{OO'} \times \vec{IH}=R^2-R'^2\)
car M se projette orthogonalement en H sur (OO')
Question
4.Conclure sur l'ensemble des points ayant même puissance par rapport à deux cercles de centre distincts.
Solution
\(2\vec{OO'} \times \vec{IH}=R^2-R'^2\)
Si \(H\in [OI]\)
\(-2OO' \times IH=R^2-R'^2\)
\(\iff IH=-\frac{R^2-R'^2}{2OO'}\)
\(\iff IH=\frac{R'^2-R^2}{2OO'}\)
Si \(H\in [IO']\)
\(2OO' \times IH=R^2-R'^2\)
\(\iff IH=\frac{R^2-R'^2}{2OO'}\)
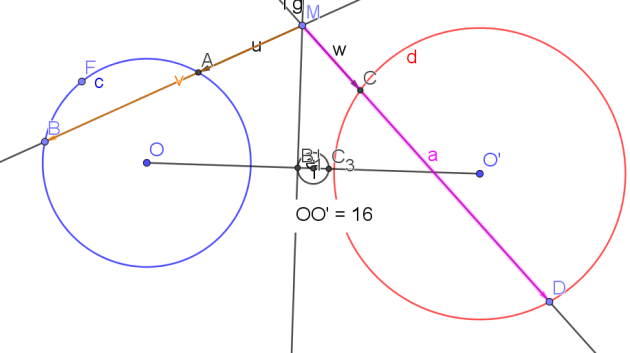
Exemple :
C(O,5) et C(O',7)
OO'=16
Si \(H\in [OI]\)
\(IH=\frac{7^2-5^2}{2\times 16}=\frac{49-25}{32}=\frac{24}{32}=\frac{3}{4}=0,75\)
Si \(H\in [IO']\)
\(IH=\frac{5^2-7'^2}{2\times 16}=\frac{25-49}{32}=\frac{-24}{32}=-\frac{3}{4}=-0,75\)
Une distance étant toujours positive donc cette deuxième valeur est impossible.
\(\color{magenta}{\text{L'ensemble cherché est donc une droite perpendiculaire à (OO') appelé axe radical des cercles (C) et (C').}}\)
Question
5. Que se passe t-il si les deux cercles sont tangents ?
Solution
\(2\vec{OO'} \times \vec{IH}=R^2-R'^2\)
Si \(H\in [OI]\)
\(-2OO' \times IH=R^2-R'^2\)
\(\iff IH=-\frac{R^2-R'^2}{2OO'}\)
Or OO'=R+R'
\(\iff IH=\frac{R'^2-R^2}{2(R+R')}\)
\(\iff IH=\frac{R'-R}{2}\)
Si \(H\in [IO']\)
\(2OO' \times IH=R^2-R'^2\)
\(\iff IH=\frac{R^2-R'^2}{2(R+R')}\)
\(\iff IH=\frac{R-R'}{2}\)
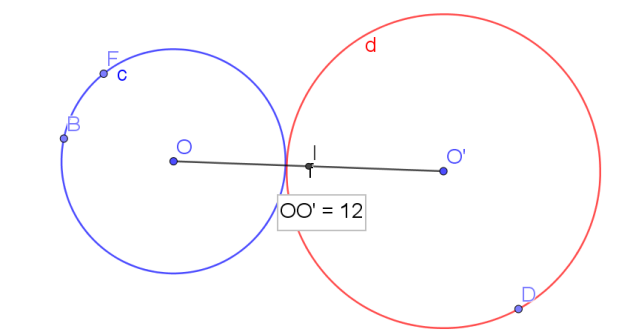
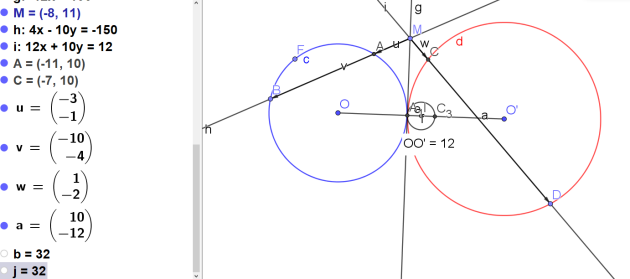
Exemple :
C(O,5) et C(O',7)
OO'=12
Si \(H\in [OI]\)
\(IH=\frac{7-5}{2}=\frac{2}{2}=1\)
Si \(H\in [IO']\)
\(IH=\frac{5-7}{2}=\frac{-2}{2}=-1\)
Une distance étant toujours positive donc cette deuxième valeur est impossible.
\(\color{magenta}{\text{L'ensemble cherché est donc une droite perpendiculaire à (OO') appelé axe radical des cercles (C) et (C').}}\)
\(\color{red}{\text{Pour deux cercles tangents, c'est la tangente commune.}}\)
Question
6. Que se passe t-il si les deux cercles sont sécants ?
Solution
\(2\vec{OO'} \times \vec{IH}=R^2-R'^2\)
Si \(H\in [OI]\)
\(-2OO' \times IH=R^2-R'^2\)
\(\iff IH=-\frac{R^2-R'^2}{2OO'}\)
Si \(H\in [IO']\)
\(2OO' \times IH=R^2-R'^2\)
\(\iff IH=\frac{R^2-R'^2}{2OO'}\)
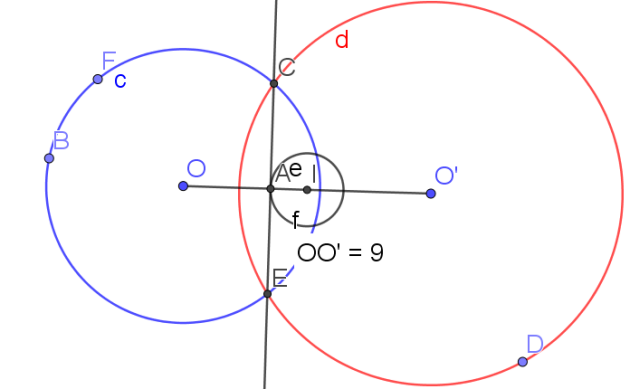
Exemple :
C(O,5) et C(O',7)
OO'=9
Si \(H\in [OI]\)
\(IH=\frac{7^2-5^2}{2\times 9}=\frac{49-25}{18}=\frac{24}{18}=\frac{4}{3}\)
Si \(H\in [IO']\)
\(IH=\frac{5^2-7^2}{2 \times 9}=\frac{-24}{18}=-\frac{4}{3}\)
Une distance étant toujours positive donc cette deuxième valeur est impossible.
\(\color{magenta}{\text{L'ensemble cherché est donc une droite perpendiculaire à (OO') appelé axe radical des cercles (C) et (C').}}\)
\(\color{\text{Pour deux cercles sécants, c'est la droite passant par les points d'intersection des deux cercles}}\)
En effet, en ces deux points, la puissance est nulle par rapport aux deux cercles.
Lorsque les cercles n'ont aucun point commun,
on se ramène au cas sécant au moyen d'un cercle auxiliaire
(cercle violet)
permettant de trouver un point J de l'axe radical des deux cercles.
On construit alors la perpendiculaire à la droite (OO') passant par le point J.
