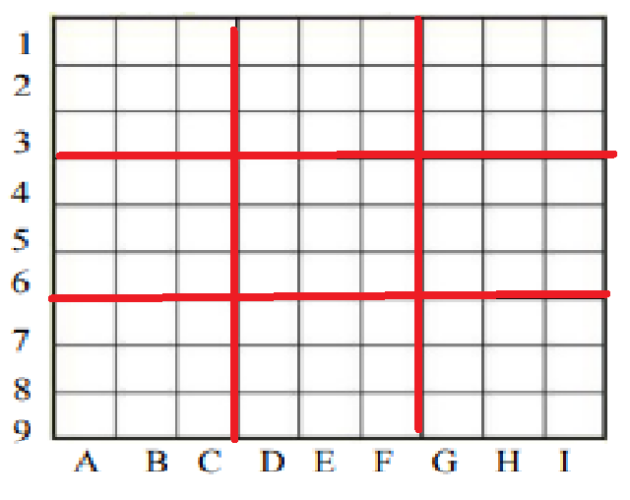
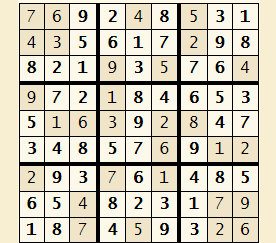
Exercice : SUDOMATHS : Produit scalaire et applications
On se place dans un repère orthonormé du plan (\(O;\vec{i} ; \vec{j}\) ) A l'aide des énigmes mathématiques suivantes, remplir les cases correspondantes. Ensuite, appliquer la méthode « classique » pour remplir les autres cases.
Question
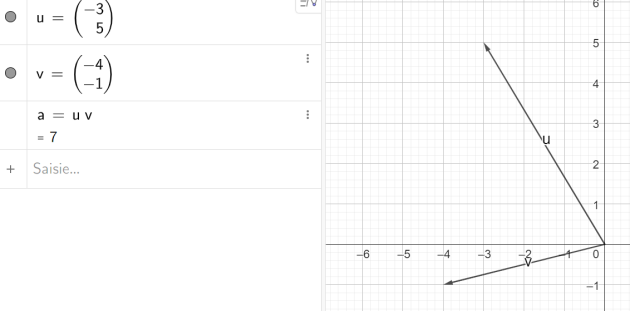
A1 : Soient \(\vec{u}\)(-3;5) et \(\vec{v}\)(-4;-1), \(\vec{u}\).\(\vec{v}\) =\(\cdots\)
Question
B1 : Sachant que AB = 3 ,AC = 2 et \(\vec{AB}.\vec{AC} \)= \(\frac{7}{2}\)
calculer \((\vec{AB} - \vec{AC} )^2 =\cdots\)
Solution
\((\vec{AB} - \vec{AC} )^2 =(\vec{AB} - \vec{AC} ).(\vec{AB} - \vec{AC} )\)
\(\iff (\vec{AB} - \vec{AC} )^2 =\vec{AB}. \vec{AB}- \vec{AB}.\vec{AC} - \vec{AC}. \vec{AB}- \vec{AC}. (-\vec{AC})\)
\(\iff (\vec{AB} - \vec{AC} )^2 =||\vec{AB}|| \times |\vec{AB}|| \times cos((\vec{AB};\vec{AB})) - \vec{AB}.\vec{AC} - \vec{AB }. \vec{AC}+ ||\vec{AC}|| \times ||\vec{AC}|| \times cos((\vec{AC};\vec{AC}))\)
\(\iff (\vec{AB} - \vec{AC} )^2 =AB \times AB \times cos(0) -2 \vec{AB}.\vec{AC} + AC \times AC \times cos(0)\)
\(\iff (\vec{AB} - \vec{AC} )^2 =AB^2-2 \times \frac{7}{2}+ AC^2\)
\(\iff (\vec{AB} - \vec{AC} )^2 =3^2-7+ 2^2\)
\(\iff (\vec{AB} - \vec{AC} )^2 =9-7+ 4=2+4=6\)
donc \(\color{magenta}{\text{B1 est 6}}\)
Question
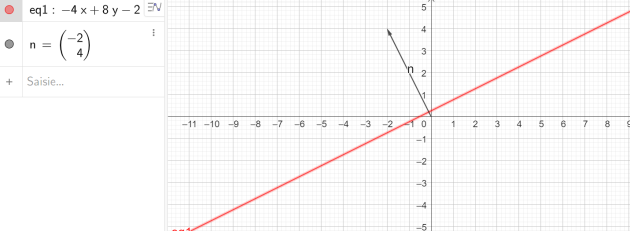
E1 : \(\vec{n}\)(-2 ;......) est un vecteur normal à la droite (d) : \(- 4x + 8y – 2 = 0\)
Solution
\(vec{n}\)(-2 ;......) est un vecteur normal à la droite (d) :
\(- 4x + 8y – 2 = 0\)
La droite (d) est aussi d'équation \(-2x+4y-1=0\) (en divisant tous les coeffeicients par 2)
\(\vec{n}.\vec{AM}\)
\(=\left (\begin{array}{c}-2\\n_y\end{array} \right) .\left (\begin{array}{c}x-x_A\\y-y_A\end{array} \right )\)
\(= -2(x-x_A)+n_y(y-y_A)\)
\(=- 2x + n_yy +2x_A-n_y \times y_A\)
Pour égaler avec l'équation de la droite (d) :
\(n_yy=4y\) donc \(n_y=4\)
Le vecteur \(\vec{n}\)(-2 ;4) est un vecteur normal à la droite (d) : \(- 4x + 8y – 2 = 0\)
donc \(\color{magenta}{\text{E1 est 4}}\)
Question
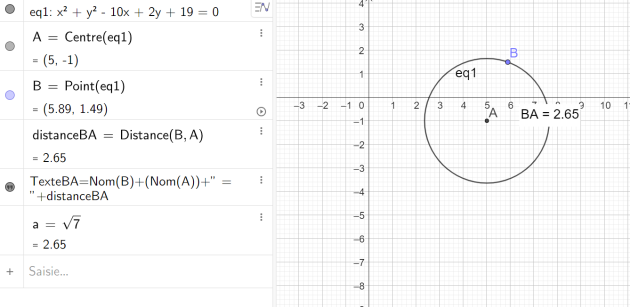
G1 : Abscisse du centre du cercle d'équation :
\(x^2 + y^2 – 10x + 2y + 19 = 0\)
Solution
\(x^2 + y^2 – 10x + 2y + 19 = 0\)
\(\iff (x-5)^2 + (y+1)^2 -25-1+ 19 = 0\)
\(\iff (x-5)^2 + (y+1)^2 -26+ 19 = 0\)
\(\iff (x-5)^2 + (y+1)^2-7 = 0\)
\(\iff (x-5)^2 + (y+1)^2=7\)
\(\iff \Omega M^2=R^2=\sqrt{7}^2\)
Le cercle d'équation
\(x^2 + y^2 – 10x + 2y + 19 = 0\)
est donc le cercle de centre \(\Omega=(5 ;-1)\) et de rayon \(\sqrt{7}\)
donc \(\color{magenta}{\text{G1 est 5}}\)
Question
A2 : Si \(\vec{u} = 2\vec{i} –5\vec{j}\) et \(\vec{v} =- 2\vec{j} –3\vec{i}\) ,
alors \(\vec{u}.\vec{v} = \cdots\)
Solution
\(\vec{u} =\left (\begin{array}{c} 2\\–5 \end{array} \right) \)et \(\vec{v} =\left (\begin{array}{c} -3\\–2 \end{array} \right)\)
alors \(\vec{u}.\vec{v} =xx'+yy'\)
\(\iff \vec{u}.\vec{v} =2 \times (-3)+(-5) \times (-2)\)
\(\iff \vec{u}.\vec{v} =-6+10\)
\(\iff \vec{u}.\vec{v} =4\)
donc \(\color{magenta}{\text{A2 est 4}}\)
Question
B2 : Si \(\vec{u}(2; \sqrt{5})\), alors \(|| \vec{u}|| =\cdots\)
Solution
\(|| \vec{u}|| =\sqrt{2^2+\sqrt{5}^2}\)
\(\iff || \vec{u}|| =\sqrt{4+5}\)
\(\iff || \vec{u}|| =\sqrt{9}\)
\(\iff || \vec{u}|| =3\)
donc \(\color{magenta}{\text{B2 est 3}}\)
Question
G2 : \((\vec{u} +\vec{v})^2\) = \(||\vec{u}||^2 + ||\vec{v}||^2 + \cdots \vec{u} . \vec{v}\)
Solution
\((\vec{u} +\vec{v})^2\)
=\((\vec{u} +\vec{v}).(\vec{u} +\vec{v})\)
\(\iff (\vec{u} +\vec{v})^2\)
=\(\vec{u}.\vec{u}+\vec{v}.\vec{u}+\vec{v}.\vec{u} +\vec{v}.\vec{v}\)
\(\iff (\vec{u} +\vec{v})^2\)
=\(||\vec{u}||.||\vec{u}||. cos((\vec{u};\vec{u}))+2\vec{u}.\vec{v}+||\vec{v}||.||\vec{v}||.cos((\vec{v};\vec{v}))\)
\(\iff (\vec{u} +\vec{v})^2\)
=\(||\vec{u}||^2. cos(0)+2\vec{u}.\vec{v}+||\vec{v}||^2.cos(0)\)
\(\iff (\vec{u} +\vec{v})^2\)
=\(||\vec{u}||^2. +2\vec{u}.\vec{v}+||\vec{v}||^2\)
donc \(\color{magenta}{\text{G2 est 2}}\)
Question
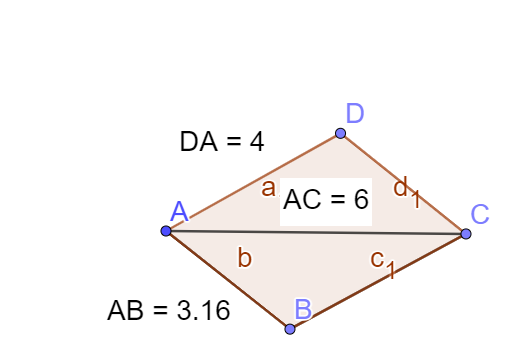
F3 : Soit ABCD un parallélogramme tel que AC= 6, AB = \(\sqrt{10}\) et AD = 4.
Calculer \(\vec{AB}. \vec{AD}\)
Solution
\(\vec{u} \vec{v}=\frac{1}{2}(||\vec{u}||^2+ ||\vec{v}||^2-||\vec{u}-\vec{v}||^2)\)
donc \(\vec{AB} \vec{AD}=\frac{1}{2}(||\vec{AB}||^2+ ||\vec{AD}||^2-||\vec{AB}-\vec{AD}||^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(AB^2+ AD^2-||\vec{AB}+\vec{DA}||^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(AB^2+ AD^2-||\vec{DA}+\vec{AB}||^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(AB^2+ AD^2-||\vec{DB}||^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(AB^2+ AD^2-DB^2)\)
La longueur DB n'est pas connue donc cette formule ne nous permet pas de conclure.
\(\vec{u} \vec{v}=\frac{1}{2}(||\vec{u}+\vec{v}||^2- ||\vec{u}||^2-||\vec{v}||^2)\)
donc \(\vec{AB} \vec{AD}=\frac{1}{2}(||\vec{AB}+\vec{AD}||^2- ||\vec{AB}||^2-||\vec{AD}||^2)\)
\(\vec{AD}=\vec{BC}\)
donc \(\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(AC^2- AB^2-AD^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(6^2- \sqrt{10}^2-4^2)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(36-10-16)\)
\(\iff \vec{AB} \vec{AD}=\frac{1}{2}(10)=5\)
donc \(\color{magenta}{\text{F3 est 5}}\)
Question
D3 : Soient \(\vec{u}\) et \(\vec{v}\) , deux vecteurs tels que : \(||\vec{u}|| \)= 10, \(||\vec{v} ||\) = 25 et \(\vec{u} .\vec{v}\) = 247.
Calculer (\(\vec{u} ,\vec{v}\) ) au degré près.
Solution
\(vec{u} .\vec{v}\) = ||\(vec{u}|| \times ||\vec{v}\)|| \times cos(\((\vec{u} ;\vec{v})\))
\(\iff 247=10 \times 25 \times cos(\)\((\vec{u} ;\vec{v})\))
\(\iff 247=250 \times cos(\)\((\vec{u} ;\vec{v})\))
\(\iff cos(\)\((\vec{u} ;\vec{v})\))\(=\frac{247}{250}\)
\(\iff \)\((\vec{u} ;\vec{v})\))\(=Arccos(\frac{247}{250}) \simeq 9\)
donc \(\color{magenta}{\text{D3 est 9}}\)
Question
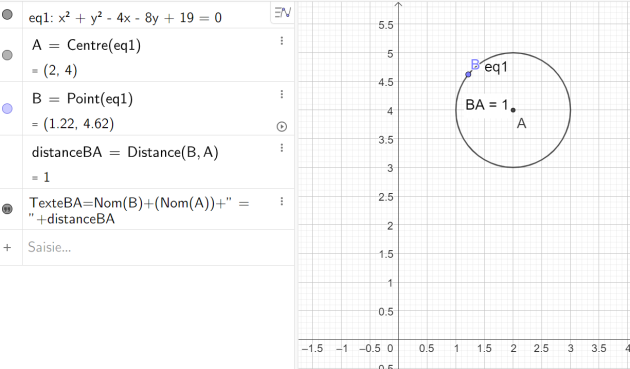
I3 : Ordonnée du centre du cercle d'équation : \(x^2 + y^2 – 4x – 8y + 19 = 0\)
Solution
\(x^2 + y^2 – 4x – 8y + 19 = 0\)
\(\iff (x-2)^2 + (y-4)^2-4-16 +19=0\)
\(\iff (x-2)^2 + (y-4)^2-1=0\)
\(\iff (x-2)^2 + (y-4)^2=1\)
\(\iff \Omega M^2=R^2=1^2\)
Le cercle d'équation
\(x^2 + y^2 – 4x – 8y + 19 = 0\)
est donc le cercle de centre \(\Omega=(2 ;4)\) et de rayon \(1\)
donc \(\color{magenta}{\text{I3 est 4}}\)
Question
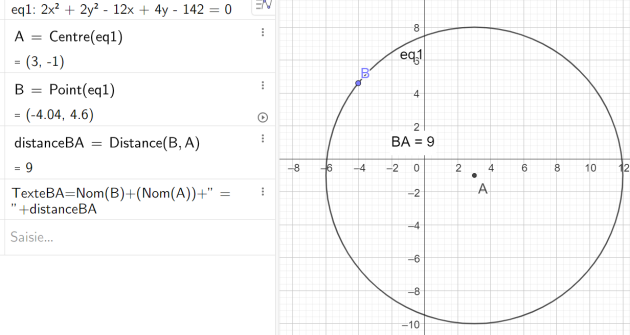
A4 : Rayon du cercle d'équation : \(2x^2 + 2y^2 – 12x + 4y – 142 = 0\)
Solution
\(2x^2 + 2y^2 – 12x + 4y – 142 = 0\)
\(\iff x^2 + y^2 – 6x + 2y – 71= 0\)
\(\iff (x-3)^2 + (y+1)^2 -9 - 1 – 71= 0\)
\(\iff (x-3)^2 + (y+1)^2 -81= 0\)
\(\iff (x-3)^2 + (y+1)^2 =81\)
\(\iff \Omega M^2=R^2=9^2\)
Le cercle d'équation
\(2x^2 + 2y^2 – 12x + 4y – 142 = 0\)
est donc le cercle de centre \(\Omega=(3 ;-1)\) et de rayon \(9\)
donc \(\color{magenta}{\text{A4 est 9}}\)
Question
B6 :\(|| \vec{u}+\vec{v} ||^2 - ||\vec{u}-\vec{v}||^2 = \cdots \vec{u} .\vec{v}\)
Solution
\(|| \vec{u}+\vec{v} ||^2=|| \vec{u}+\vec{v} ||.|| \vec{u}+\vec{v} ||.cos(( \vec{u}+\vec{v}, \vec{u}+\vec{v}))=( \vec{u}+\vec{v})^2\)
or \(( \vec{u}+\vec{v}).( \vec{u}+\vec{v})=\vec{u}.\vec{u}+ \vec{u}.\vec{v}+\vec{v}.\vec{u}+\vec{v}.\vec{v}\)
\(\iff ( \vec{u}+\vec{v}).( \vec{u}+\vec{v})=||\vec{u}||^2+2 \vec{u}.\vec{v}+||\vec{v}||^2\)
donc \(||\vec{u}+\vec{v}||2 = ||\vec{u}||^2+2 \vec{u}.\vec{v}+||\vec{v}||^2\)
\(|| \vec{u}-\vec{v} ||^2=|| \vec{u}-\vec{v} ||.|| \vec{u}-\vec{v} ||.cos(( \vec{u}-\vec{v}, \vec{u}-\vec{v}))=( \vec{u}-\vec{v})^2\)
or \(( \vec{u}-\vec{v}).( \vec{u}-\vec{v})=\vec{u}.\vec{u}- \vec{u}.\vec{v}-\vec{v}.\vec{u}+(-\vec{v}).(-\vec{v})\)
\(\iff ( \vec{u}-\vec{v}).( \vec{u}-\vec{v})=||\vec{u}||^2-2 \vec{u}.\vec{v}+||\vec{v}||^2\)
donc \(||\vec{u}-\vec{v}||2 = ||\vec{u}||^2-2 \vec{u}.\vec{v}+||\vec{v}||^2\)
Finalement \(|| \vec{u}+\vec{v} ||^2 - ||\vec{u}-\vec{v}||^2 =( ||\vec{u}||^2+2 \vec{u}.\vec{v}+||\vec{v}||^2)-(||\vec{u}||^2-2 \vec{u}.\vec{v}+||\vec{v}||^2)\)
\(\iff || \vec{u}+\vec{v} ||^2 - ||\vec{u}-\vec{v}||^2 = ||\vec{u}||^2+2 \vec{u}.\vec{v}+||\vec{v}||^2-||\vec{u}||^2+2 \vec{u}.\vec{v}-||\vec{v}||^2\)\(\)
\(\iff || \vec{u}+\vec{v} ||^2 - ||\vec{u}-\vec{v}||^2 = 4\vec{u}.\vec{v}\)
donc \(\color{magenta}{\text{B4 est 4}}\)
Question
D4 : Soit \(\vec{v}\) (\(-\frac{1}{2} ; \frac{\sqrt{3}}{2}\) ), \(||\vec{v}|| =\cdots\)
Solution
\(||\vec{v}|| =\sqrt{x^2+y^2}\)
\(\iff ||\vec{v}|| =\sqrt{(-\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}\)
\(\iff ||\vec{v}|| =\sqrt{\frac{1}{4}+\frac{3}{4}}\)
\(\iff ||\vec{v}|| =\sqrt{\frac{4}{4}}\)
\(\iff ||\vec{v}|| =\sqrt{1}\)
\(\iff ||\vec{v}|| =1\)
donc \(\color{magenta}{\text{D4 est 1}}\)
Question
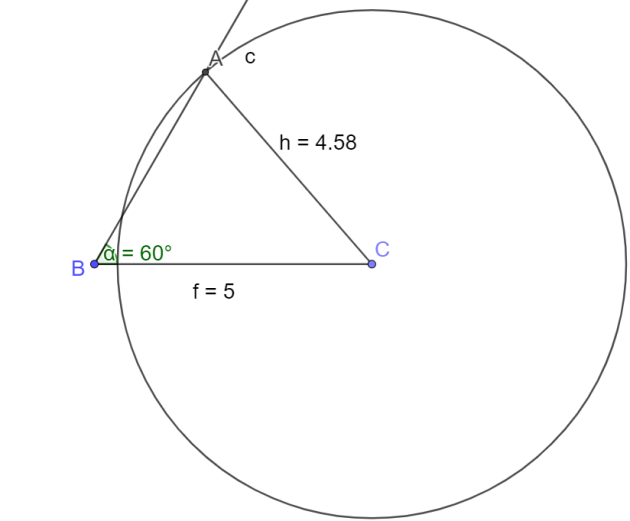
B5 : ABC est un triangle tel que BC = 5 cm, AC =\sqrt{21} cm et \(\widehat{ABC}\) = 60°.
\(AB=\cdots\)
Solution
On utilise le théorème d'Al-Khasi dans le triangle ABC :
\(AC^2=BC^2+BA^2-2BC \times BA \cos(\widehat{ABC})\)
\(\iff \sqrt{21}^2=5^2+BA^2-2 \times 5 \times BA \cos(60)\)
\(\iff 21=25+BA^2-2 \times 5 \times BA \times \frac{1}{2}\)
\(\iff 21=25+BA^2-5 BA\)
\(\iff 0=BA^2-5 BA+4\)
\(\iff BA^2-5 BA+4=0\)
On doit résoudre une équation du second degré :
\(a=1\) \(b=-5\) \(c=4\)
Calcul du discriminant :
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-5)^2-4 \times 1 \times 4\)
\(\iff \Delta=25-16\)
\(\iff \Delta=9\)
Comme \(\Delta>0\),
l'équation \(BA^2-5 BA+4=0\) admet deux solutions :
\(\begin{cases}BA_1=\frac{-b-\sqrt{\Delta}}{2a}\\BA_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}BA_1=\frac{-(-5)-\sqrt{9}}{2 \times 1}\\BA_2=\frac{-(-5)+\sqrt{9}}{2 \times 1}\end{cases}\)
\(\iff \begin{cases}BA_1=\frac{5-3}{2}\\BA_2=\frac{5+3}{2}\end{cases}\)
\(\iff \begin{cases}BA_1=\frac{2}{2}\\BA_2=\frac{8}{2}\end{cases}\)
\(\iff \begin{cases}BA_1=\frac{2}{2}\\BA_2=\frac{8}{2}\end{cases}\)
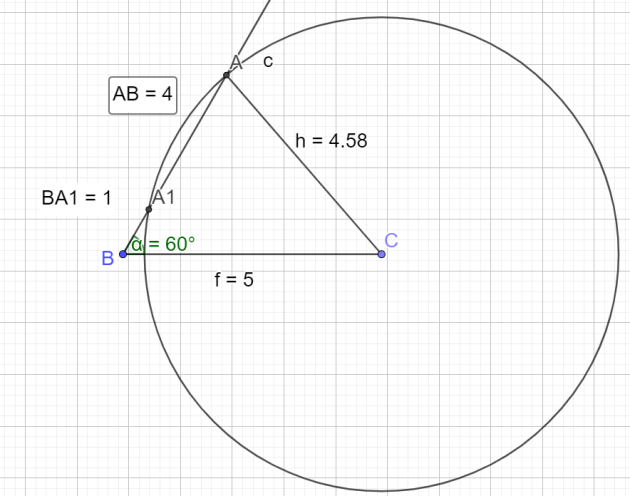
\(\iff \begin{cases}BA_1=1\\BA_2=4\end{cases}\)
donc \(\color{magenta}{\text{B5 est 1}}\) car la valeur de la case B4 est 4 (même colonne)
Question
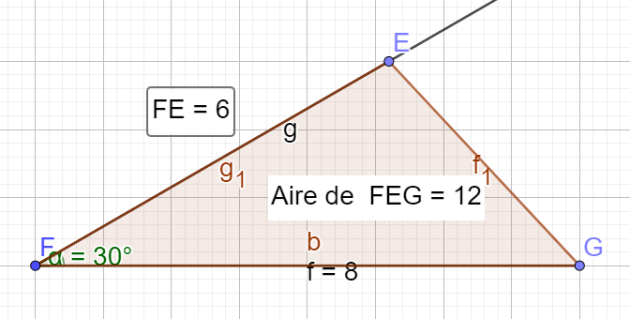
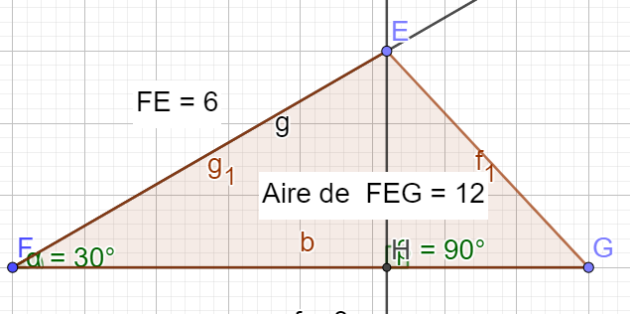
C5 : EFG est un triangle d'aire 12 \(cm^2\) .
FG = 8 cm et \(\widehat{EFG}\) = 30°.
\(EF = \cdots\)
Solution
\(\color{magenta}{\text{1ère méthode :}}\)
\(\vec{FE}.\vec{FG}=||\vec{FE}|| \times ||\vec{FG}|| \times cos((\vec{FE} ;\vec{FG}))\)
\(\iff \vec{FE}.\vec{FG}=FE \times 8 \times cos(30)\)
\(\iff \vec{FE}.\vec{FG}=FE \times 8 \times \frac{\sqrt{3}}{2}\)\(\)
\(\iff \vec{FE}.\vec{FG}=4\sqrt{3}FE\)
\(\color{magenta}{\text{2ème méthode :}}\)
\(\vec{FE}.\vec{FG}=||\vec{FH}|| \times ||\vec{FG}||\)
\(\iff \vec{FE}.\vec{FG}=FH \times 8\)
Aire du triangle :
\(\frac{Base \times Hauteur}{2}=\frac{FG \times EH}{2}=12\)
\(\iff \frac{8 \times EH}{2}=12\)
\(\iff 8EH=24\)
\(\iff EH=3\)
On utilise les formules de trigonométrie dans le triangle EFH rectangle en H
\(tan(\widehat{EFH})=\frac{côté opposé}{côté adjacent}\)
\(\iff tan(30)=\frac{EH}{FH}=\frac{3}{FH}\)\(\)
\(\iff \frac{tan(30)}{1}=\frac{3}{FH}\)
On effectue le produit en croix d'où :
\(tan(30) \times FH=3 \times 1=3\)
\(\iff FH=\frac{3}{tan(30)}\)
or \(tan(30)=\frac{sin(30)}{cos(30)}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}\)
\(\iff tan(30)=\frac{1}{2} \times \frac{2}{\sqrt{3}}\)
\(\iff tan(30)=\frac{1}{\sqrt{3}}\)
\(\iff FH=\frac{3}{\frac{1}{\sqrt{3}}}\)
\(\iff FH=3 \times \frac{\sqrt{3}}{1}\)
\(\iff FH=3\sqrt{3}\)
\(\iff \vec{FE}.\vec{FG}=3\sqrt{3} \times 8=24\sqrt{3}\)
Finalement, on obtient l'égalité :\(\vec{FE}.\vec{FG}=4\sqrt{3}FE=24\sqrt{3}\)
\(\iff 4\sqrt{3}FE=24\sqrt{3}\)
\(\iff FE=\frac{24\sqrt{3}}{4\sqrt{3}}=6\)
donc \(\color{magenta}{\text{C5 est 6}}\)
Question
D5 : En remarquant que \(\frac{π}{4} + \frac{π}{6} = \frac{5π}{12}\)
on peut montrer que :
\(cos(\frac{5π}{12}) =\frac{\sqrt{2}×(\sqrt{\cdots}−1)}{4}\)
Solution
\(\frac{π}{4} + \frac{π}{6} =\frac{3π}{12} + \frac{2π}{12}=\frac{5π}{12}\)
\(cos(\frac{5π}{12})=cos(\frac{π}{4} + \frac{π}{6})\)
\(\iff cos(\frac{5π}{12})=cos(\frac{π}{4})cos(\frac{π}{6})-sin(\frac{π}{4})sin(\frac{π}{6})\)
\(\iff cos(\frac{5π}{12})=\frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2} \times \frac{1}{2}\)
\(\iff cos(\frac{5π}{12})=\frac{\sqrt{2} \times \sqrt{3}}{4}-\frac{\sqrt{2}}{4}\)
\(\iff cos(\frac{5π}{12})=\frac{\sqrt{2} \times (\sqrt{3}-1)}{4}\)
donc \(\color{magenta}{\text{D5 est 3}}\)
Question
F5 : \(sin(2x) =.........sin(x) × cos(x)\)
Solution
\(sin(2x) =2sin(x) × cos(x)\)
donc \(\color{magenta}{\text{F5 est 2}}\)
Question
G5 : IJK est un triangle isocèle et rectangle en I tel que :
IK = \(2\sqrt{2}\) cm et JK = 4 cm
\(\vec{JI} .\vec{JK} =\cdots\)
Solution
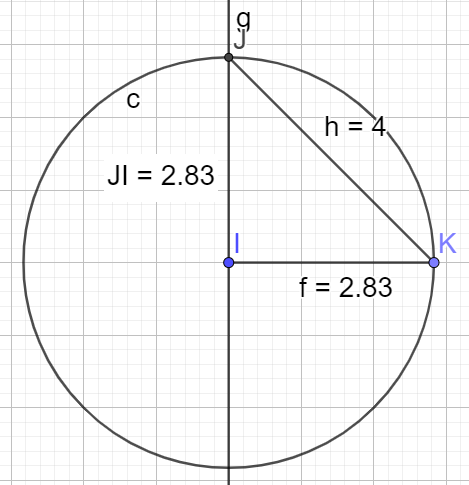
\(\vec{JI} .\vec{JK} =\vec{JI} .\vec{JI}\)
car le point I est le projeté orthogonal du point K sur la droite (JI)
\(\iff \vec{JI} .\vec{JK} =||\vec{JI}|| \times ||\vec{JI}|| \times cos((\vec{JI};\vec{JI}))\)
\(\iff \vec{JI} .\vec{JK} =||\vec{JI}||^2 \times cos(0)\)
\(\iff \vec{JI} .\vec{JK} =JI^2 \times 1\)
\(\iff \vec{JI} .\vec{JK} =JI^2=(2\sqrt{2})^2=8\)
donc \(\color{magenta}{\text{G5 est 8}}\)
Question
H5 : Soit la droite (\(d_1\)) :\( x – y + 1 = 0\)
et \((d_2)\) la droite dont une équation cartésienne est de la forme :
\(ax + by + c = 0\).
Sachant que (\(d_2\)) ⊥ (\(d_1\)) et \(A(3;1) ∈ (d_2)\) valeur du coefficient \(c =\cdots\)
Solution
(\(d_1\)) :\( x – y + 1 = 0 \iff y=x+1\)
Un vecteur directeur de la droite (\(d_1\)) est \(\left ( \begin{array}{c}1\\m\end{array} \right )=\left ( \begin{array}{c}1\\1\end{array} \right )\)
\((d_2)\) la droite d'équation cartésienne :
\(ax + by + c = 0\)
\(\iff by= -ax-c\)
\(\iff y= -\frac{a}{b}x-\frac{c}{b}\)
Un vecteur directeur de la droite (\(d_2\)) est \(\left ( \begin{array}{c}1\\m\end{array} \right )=\left ( \begin{array}{c}1\\-\frac{a}{b}\end{array} \right )\)
Les deux droites sont orthogonales donc :
\(\left ( \begin{array}{c}1\\1\end{array} \right ).\left ( \begin{array}{c}1\\-\frac{a}{b}\end{array} \right )=0\)
\(\iff 1 \times 1+1 \times (-\frac{a}{b})=0\)
\(\iff 1-\frac{a}{b}=0\)
\(\iff -\frac{a}{b}=-1\)
\(\iff \frac{a}{b}=1\)
\(\iff a=b\)
L'équation réduite de la droite (\(d_2\)) est donc
\(y= -\frac{a}{b}x-\frac{c}{b}\)
\(\iff y= -\frac{a}{a}x-\frac{c}{a}\)
\(\iff y= -x-\frac{c}{a}\)
\(A(3 ;1) \in (d_2)\)
\(\iff 1=-3-\frac{c}{a}\)
\(\iff 4=-\frac{c}{a}\)
\(\iff -\frac{c}{a}=4\)
\(\iff -\frac{c}{a}=4\)
\(\iff \frac{c}{a}=-4\)
\(\iff c=-4a\)
Une équation cartésienne de la droite (\(d_2\)) est :
\(ax+by+c=0\)
\(\iff ax+ay-4a=0\)
\(\iff ax+ay-4a=0\)
\(c=-4a\in [0 ;9]\)
si et seulement si \(a=-1\) :
\(c=4\)
une équation cartésienne de la droite (\(d_2\)) est :
\(-x-y+4=0\)
ou \(a=-2\)
\(c=8\)
une équation cartésienne de la droite (\(d_2\)) est :
\(-2x-2y+8=0\)
donc \(\color{magenta}{\text{H5 est 4 }}\) car la valeur de la case G5 est 8
Question
F6 : Soient A et B, deux points, tels que AB = 2 cm. Soit un point M tel que :
\(MA^2 + MB^2 = 74\).
I est le milieu du segment [AB]
\(MI = \cdots\)
Solution
\(MA^2 + MB^2 = 74\)
\(MA^2=(\vec{MI}+\vec{IA})^2=(\vec{MI}+\vec{IA}).(\vec{MI}+\vec{IA})\)
\(\iff MA^2=\vec{MI}.\vec{MI}+\vec{MI}.\vec{IA}+\vec{IA}.\vec{IA}+\vec{IA}.\vec{IA}\)\(\)
\(\iff MA^2=||\vec{MI}|| \times ||\vec{MI}|| \times cos((\vec{MI};\vec{MI}))+2\vec{MI}.\vec{IA}+||\vec{IA}|| \times ||\vec{IA}||\times cos((\vec{IA};\vec{IA}))\)\(\)
\(\iff MA^2=||\vec{MI}||^2\times cos(0)+2\vec{MI}.\vec{IA}+||\vec{IA}||^2 \times cos(0)\)\(\)
\(\iff MA^2=MI^2+2\vec{MI}.\vec{IA}+IA^2\)
\(IA=IB=\frac{AB}{2}=\frac{2}{2}=1\)\(\)
\(\iff MA^2=MI^2+2\vec{MI}.\vec{IA}+1^2\)\(\)
\(\iff MA^2=MI^2+2\vec{MI}.\vec{IA}+1\)
\(MB^2=(\vec{MI}+\vec{IB})^2=(\vec{MI}+\vec{IB}).(\vec{MI}+\vec{IB})\)
\(\iff MB^2=\vec{MI}.\vec{MI}+\vec{MI}.\vec{IB}+\vec{IB}.\vec{IB}+\vec{IB}.\vec{IB}\)\(\)
\(\iff MB^2=||\vec{MI}|| \times ||\vec{MI}|| \times cos((\vec{MI};\vec{MI}))+2\vec{MI}.\vec{IB}+||\vec{IB}|| \times ||\vec{IB}||\times cos((\vec{IB};\vec{IB}))\)\(\)\(\)
\(\iff MB^2=||\vec{MI}||^2\times cos(0)+2\vec{MI}.\vec{IB}+||\vec{IB}||^2 \times cos(0)\)\(\)\(\)
\(\iff MB^2=MI^2+2\vec{MI}.\vec{IB}+IB^2\)
\(IA=IB=\frac{AB}{2}=\frac{2}{2}=1\)\(\)\(\)
\(\iff MB^2=MI^2+2\vec{MI}.\vec{IB}+1^2\)\(\)\(\)
\(\iff MB^2=MI^2+2\vec{MI}.\vec{IB}+1\)
\(MA^2 + MB^2 = 74\)
\(\iff MI^2+2\vec{MI}.\vec{IA}+1+MI^2+2\vec{MI}.\vec{IB}+1=74\)
\(\iff 2MI^2+\vec{MI}.(\vec{IA}+\vec{IB})+2=74\)
Or \(\vec{IA}=-\vec{IB}\)
donc \(\vec{IA}+\vec{IB}=\vec{0}\)
\(\iff 2MI^2+2=74\)
\(\iff 2MI^2=72\)\(\)
\(\iff MI^2=36\)
\(\iff MI=6\)
L'ensemble des points est le cercle de centre I milieu du segment [AB] et de rayon 6
donc \(\color{magenta}{\text{F6 est 6}}\)
Question
H6 : \(\vec{n}\left(\begin{array}{c}5\\\cdots\end{array} \right )\)et \(\vec{u}\left(\begin{array}{c}-\frac{9}{2} \\\ \frac{45}{2}\end{array} \right )\) sont orthogonaux
Solution
\(\vec{n}( 5 ;x )\) et \(\vec{u} (-\frac{9}{2} ; \frac{45}{2} )\) sont orthogonaux
\(\vec{n}.\vec{u}=0\)
\(\iff 5 \times (-\frac{9}{2})+x \times \frac{45}{2}=0\)
\(\iff -\frac{45}{2}+\frac{45}{2}x=0\)
\(\iff \frac{45}{2}x=\frac{45}{2}\)
\(\iff x=1\)
donc \(\color{magenta}{\text{H6 est 1}}\)
Question
I6 : \(cos(x) = - 1 + \cdots cos^2(\frac{x}{2})\)
Solution
\(cos(x) =cos(\frac{x}{2}+\frac{x}{2})=cos(\frac{x}{2})cos(\frac{x}{2})-sin(\frac{x}{2})sin(\frac{x}{2})\)
\(\iff cos(x) =cos^2(\frac{x}{2})-sin^2(\frac{x}{2})\)
\(cos^2(frac{x}{2})+sin^2(\frac{x}{2})=1\)
\(\iff cos(x) =cos^2(\frac{x}{2})-(1-cos^2(\frac{x}{2}))\)
\(\iff cos(x) =cos^2(\frac{x}{2})-1+cos^2(\frac{x}{2})\)
\(\iff cos(x) =2cos^2(\frac{x}{2})-1\)
\(\iff cos(x) =-1+2cos^2(\frac{x}{2})\)
donc \(\color{magenta}{\text{I6 est 2}}\)
Question
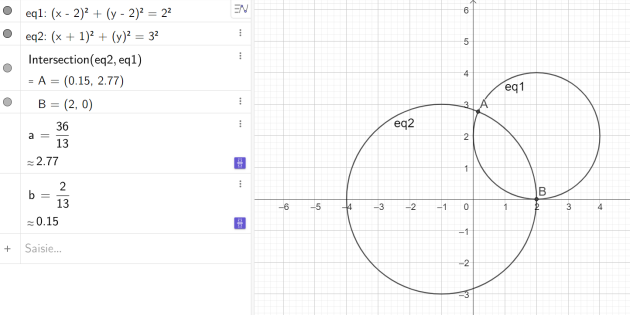
A7 : On considère le cercle de centre A(2;2) et de rayon 2 et le cercle de centre B(-1;0) et de rayon 3.
Ces deux cercles ont deux points d'intersection dont l'un possède une abscisse entière (et pas l'autre).
Cette abscisse=....
Solution
Cercle de centre A(2;2) et de rayon 2 : \((x-2)^2+(y-2)^2=2^2 \iff (x-2)^2+(y-2)^2=4 \iff x^2-4x+4+y^2-4y+4=4\iff x^2-4x+y^2-4y+4=0\)
Cercle de centre B(-1;0) et de rayon 3 :\((x-(-1))^2+(y-0)^2=3^2 \iff (x+1)^2+y^2=9 \iff x^2+2x+y^2-8=0\)
\(\begin{cases}x^2-4x+y^2-4y+4=0\\x^2+2x+y^2-8=0\end{cases}\)
L1-L2 :\(-6x-4y+12=0 \iff -4y=6x-12\iff y=-1,5x+3\)
On remplace dans la seconde équation \(y\) par cette expression :
\(x^2+2x+(-1,5x+3)^2-8=0\)
\(\iff x^2+2x+(-1,5x)^2+2\times (-1,5x)\times 3+3^2-8=0\)
\(\iff x^2+2x+2,25x^2-9x+9-8=0\)\(\)
\(\iff 3,25x^2-7x+1=0\)
\(\iff 13x^2-28x+4=0\)
\(a=13\) \(b=-28\) \(c=4\)
\(\Delta=b^2-4ac=(-28)^2-4\times 13 \times 4\)
\(\iff \Delta=784-208\)
\(\iff \Delta=576\)
Comme \(\Delta>0\), l'équation \(13x^2-28x+4=0\) admet deux solutions :
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-28)-\sqrt{576}}{2 \times 13}\\x_2=\frac{-(-28)+\sqrt{576}}{2 \times 13 }\end{cases}\)\(\)
\(\iff \begin{cases}x_1=\frac{28-24}{26}\\x_2=\frac{28+24}{26}\end{cases}\)\(\)
\(\iff \begin{cases}x_1=\frac{4}{26}\\x_2=\frac{52}{26}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{2}{13}\\x_2=2\end{cases}\)
Calcul de l'ordonnée du point d'intersection d'abscisse \(x_1=\frac{2}{13}:\)
\(y=-1,5 \times \frac{2}{13} +3\)\(\)
\(\iff y=-\frac{3}{13} +3\)\(\)
\(\iff y=-\frac{3}{13} +\frac{3}{1}\)\(\)
\(\iff y=-\frac{3}{13} +\frac{39}{13}\)\(\)
\(\iff y=\frac{36}{13}\)
Un point d'intersection des deux cercles est le point de coordonnées \((\frac{2}{13} ;\frac{36}{13})\)
Calcul de l'ordonnée du point d'intersection d'abscisse \(x_2=2:\)\(\)
\(y=-1,5 \times 2+3\)
\(\iff y=-3+3\)
\(\iff y=0\)
Un point d'intersection des deux cercles est le point de coordonnées \((2 ;0)\)
donc \(\color{magenta}{\text{A7 est 2}}\)