Exercice : Vecteurs Colinéaires -Points Alignés
Dans un repère \((O;\vec{i} \vec{j})\),
on donne les points A(-2 ; -2),B(4 ; -3)et C(\(\frac{3}{2}\) ;2)
Question
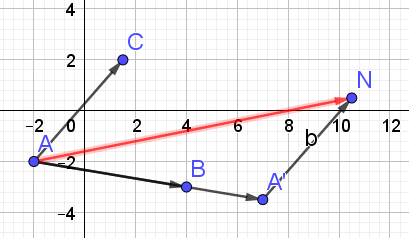
1.Construire le point N tel que \(\vec{AN}=\frac{3}{2} \vec{AB}+\vec{AC}\).
On laissera visible les traits de construction.
Question
2.Soit P le point tel que \(3\vec{PB}+2\vec{PC}=\vec{0}\)
a. Montrer que \(\vec{BP}=\frac{2}{5} \vec{BC}\)
Solution
\(3\vec{PB}+2\vec{PC}=\vec{0}\)
Par la relation de Chasles :
\(\vec{PC}=\vec{PB}+\vec{BC}\)
donc
\(3\vec{PB}+2(\vec{PB}+\vec{BC})=\vec{0}\)
\(\iff 3\vec{PB}+2\vec{PB}+2\vec{BC}=\vec{0}\)
\(\iff 5\vec{PB}+2\vec{BC}=\vec{0}\)
\(\iff \vec{PB}=-\frac{2}{5}\vec{BC}\)
\(\iff -\vec{BP}=-\frac{2}{5}\vec{BC}\)
\(\iff \vec{BP}=\frac{2}{5}\vec{BC}\)
Question
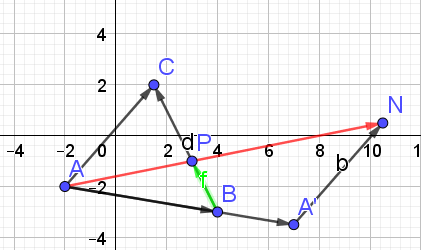
b. Placer P.
Question
c.Que peut-on conjecturer pour les points A, N et P ?
Solution
On peut conjecturer que les points A, N et P sont alignés.
Question
3. Calculer les coordonnées des points N et P.
Solution
\(\vec{AN}=\frac{3}{2} \vec{AB}+\vec{AC}\)
\(\vec{AN}=\left(\begin{array}{c}x_N-x_A\\y_N-y_A\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}x_N-(-2)\\y_N-(-2)\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}x_N+2\\y_N+2\end{array}\right)\)
\(\vec{AB}=\left(\begin{array}{c}x_B-x_A\\y_B-y_A\end{array}\right)\)
\(\iff \vec{AB}=\left(\begin{array}{c}4-(-2)\\-3-(-2)\end{array}\right)\)
\(\iff \vec{AB}=\left(\begin{array}{c}4+2\\-3+2\end{array}\right)\)
\(\iff \vec{AB}=\left(\begin{array}{c}6\\-1\end{array}\right)\)
\(\vec{AC}=\left(\begin{array}{c}x_C-x_A\\y_C-y_A\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}\frac{3}{2}-(-2)\\2-(-2)\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}\frac{3}{2}+2\\2+2\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}\frac{3}{2}+\frac{4}{2}\\4\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}\frac{7}{2}\\4\end{array}\right)\)
\(\vec{AN}=\frac{3}{2} \left(\begin{array}{c}6\\-1\end{array}\right)+\left(\begin{array}{c}\frac{7}{2}\\4\end{array}\right)\)
\(\iff \vec{AN}= \left(\begin{array}{c}\frac{18}{2}\\-\frac{3}{2}\end{array}\right)+\left(\begin{array}{c}\frac{7}{2}\\4\end{array}\right)\)
\(\iff \vec{AN}= \left(\begin{array}v\frac{18}{2}+\frac{7}{2}\\-\frac{3}{2}+4\end{array}\right)\)
\(\iff \vec{AN}=\left( \begin{array}{c}\frac{25}{2}\\-\frac{3}{2}+\frac{8}{2}\end{array}\right)\)
\(\iff \vec{AN}=\left( \begin{array}{c}\frac{25}{2}\\\frac{5}{2}\end{array}\right)\)
\(\vec{AN}=\left(\begin{array}{c}x_N+2\\y_N+2\end{array}\right)\)
\(\vec{AN}=\left(\begin{array}{c}\frac{25}{2}\\\frac{5}{2}\end{array}\right)\)
\(\iff \begin{cases}x_N+2=\frac{25}{2}\\y_N+2=\frac{5}{2}\end{cases}\)
\(\iff \begin{cases}x_N=\frac{25}{2}-2\\y_N=\frac{5}{2}-2\end{cases}\)
\(\iff \begin{cases}x_N=\frac{25}{2}-\frac{4}{2}\\y_N=\frac{5}{2}-\frac{4}{2}\end{cases}\)
\(\iff \begin{cases}x_N=\frac{21}{2}\\y_N=\frac{1}{2}\end{cases}\)
\(\vec{BP}=\frac{2}{5}\vec{BC}\)
\(\vec{BP}=\left(\begin{array}{c}x_P-x_B\\y_P-y_P\end{array}\right)\)
\(\iff \vec{BP}=\left(\begin{array}{c}x_P-4\\y_P-(-3)\end{array}\right)\)
\(\iff \vec{BP}=\left(\begin{array}{c}x_P-4\\y_P+3\end{array}\right)\)
\(\vec{BC}=\left(\begin{array}{c}x_C-x_B\\y_C-y_B\end{array}\right)\)
\(\iff \vec{BC}=\left(\begin{array}{c}\frac{3}{2}-4\\2-(-3)\end{array}\right)\)
\(\iff \vec{BC}=\left(\begin{array}{c}\frac{3}{2}-4\\2+3\end{array}\right)\)
\(\iff \vec{BC}=\left(\begin{array}{c}\frac{3}{2}-\frac{8}{2}\\5\end{array}\right)\)
\(\iff \vec{BC}=\left(\begin{array}{c}\frac{-5}{2}\\5\end{array}\right)\)
\(\vec{BP}=\frac{2}{5}\vec{BC}\)
\(\iff \vec{BP}=\left(\begin{array}{c}x_P-4\\y_P+3\end{array}\right)=\frac{2}{5}(\left(\begin{array}{c}\frac{-5}{2}\\5\end{array}\right)\)
\(\iff \begin{cases}x_P-4=\frac{2}{5} \times \frac{-5}{2} \\y_P+3=\frac{2}{5} \times 5\end{cases}\)
\(\iff \begin{cases}x_P-4=-1 \\y_P+3=2\end{cases}\)
\(\iff \begin{cases}x_P=-1+4 \\y_P=2-3\end{cases}\)
\(\iff \begin{cases}x_P=3 \\y_P=-1\end{cases}\)
Question
4. Démontrer votre conjecture de la question 2. c.-
Solution
\(\vec{AP}=\left(\begin{array}[c]x_P-x_A\\y_P-y_A\end{array}\right)\)
\(\iff \vec{AP}=\left(\begin{array}{c}3-(-2)\\-1-(-2)\end{array}\right)\)
\(\iff \vec{AP}=\left(\begin{array}{c}3+2\\-1+2\end{array}\right)\)
\(\iff \vec{AP}=\left(\begin{array}{c}5\\1\end{array}\right)\)
\(\vec{AN}=\left(\begin{array}{c}x_N-x_A\\y_N-y_A\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}\frac{21}{2}-(-2)\\\frac{1}{2}-(-2)\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}\frac{21}{2}+2\\\frac{1}{2}+2\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}\frac{21}{2}+\frac{4}{2}\\\frac{1}{2}+\frac{4}{2}\end{array}\right)\)
\(\iff \vec{AN}=\left(\begin{array}{c}\frac{25}{2}\\\frac{5}{2}\end{array}\right)\)
\(\vec{AN}=\frac{5}{2}\vec{AP}\)
\(\vec{AP} \Gamma \vec{AN} =\left(\begin{array}{c}5\\1\end{array}\right) \gamma \left(\begin{array}{c}\frac{25}{2}\\\frac{5}{2}\end{array}\right)\) (Produit en croix)
\(\vec{AP} \gamma \vec{AN} =5 \times \frac{5}{2}- 1 \times \frac{25}{2}=0\)
Les deux vecteurs \(\vec{AP}\) et \(\vec{AN}\) sont donc colinéaires
et donc les points A, P et N sont alignés.