Exercice : Vecteurs Colinéaires -Points Alignés 2
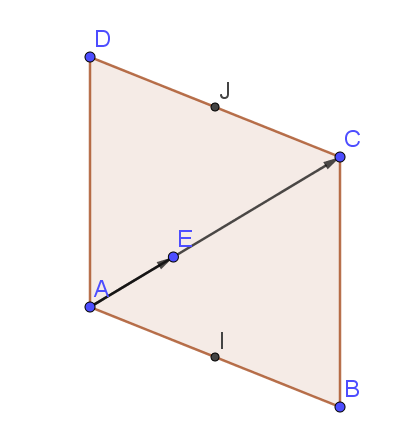
ABCD est un parallélogramme.
E est le point tel que \(\vec{AE}=\frac{1}{3}\vec{AC}\),
I est le milieu de [AB],
J est le milieu de [DC].
On considère le repère (A, \(\vec{AB}\), \(\vec{AD}\))
Question
Faire une figure que vous compléterez au fur et à mesure de l'exercice.
Question
a. Donner, sans justifier, les coordonnées des points A, B, D et C dans ce repère.
Solution
A(0, ;0)
B(1 ;0)
D(0 ;1)
C(1 ;1)
Question
b. Calculer les coordonnées des points E, I et J.
Solution
\(\vec{AE}=\frac{1}{3}\vec{AD}\)
\(\iff \left(\begin{array}{c}x_E-x_A\\y_E-y_A\end{array}\right)=\frac{1}{3}\left(\begin{array}{c}x_D-x_A\\y_D-y_A\end{array}\right)\)
\(\iff \left(\begin{array}{c}x_E-0\\y_E-0\end{array}\right)=\frac{1}{3}(\left(\begin{array}{c}x_D-0\\y_D-0\end{array}\right)\)
\(\iff \left(\begin{array}{c}x_E\\y_E\end{array}\right)=\frac{1}{3}(\left(\begin{array}{c}x_D\\y_D\end{array}\right)\)
\(\iff \left(\begin{array}{c}x_E\\y_E\end{array}\right)=\frac{1}{3}(\left(\begin{array}{c}1\\1\end{array}\right)\)
donc \(E(\frac{1}{3} ;\frac{1}{3})\)
\(\begin{cases}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{0+1}{2}\\y_I=\frac{0+0}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{1}{2}\\y_I=\frac{0}{2}\end{cases}\)
donc \(I(\frac{1}{2},0)\)
\(\begin{cases}x_J=\frac{x_C+x_D}{2}\\y_J=\frac{y_C+y_D}{2}\end{cases}\)
\(\iff \begin{cases}x_J=\frac{1+0}{2}\\y_J=\frac{1+1}{2}\end{cases}\)
\(\iff \begin{cases}x_J=\frac{1}{2}\\y_J=1\end{cases}\)
donc \(J(\frac{1}{2},1)\)
Question
3.Démontrer que les points I, E et D sont alignés.
Solution
\(\vec{EI}=\left(\begin{array}{c}x_I-x_E\\y_I-y_E\end{array}\right)\)
\(\iff \vec{EI}=\left(\begin{array}{c}\frac{1}{2}-\frac{1}{3}\\0-\frac{1}{3}\end{array}\right)\)
\(\iff \vec{EI}=\left(\begin{array}{c}\frac{3}{6}-\frac{2}{6}\\\}-\frac{1}{3}\end{array}\right)\)
\(\iff \vec{EI}=\left(\begin{array}{c}\frac{1}{6}\\-\frac{1}{3}\end{array}\right)\)
\(\vec{ED}=\left(\begin{array}{c}x_D-x_E\\y_D-y_E\end{array}\right)\)
\(\iff \vec{ED}=\left(\begin{array}{c}0-\frac{1}{3}\\1-\frac{1}{3}\end{array}\right)\)
\(\iff \vec{ED}=\left(\begin{array}{c}-\frac{1}{3}\\\frac{2}{3}\end{array}\right)\)
\(\vec{ED} \gamma \vec{EI}\)
\(=\left(\begin{array}{c}-\frac{1}{3}\\\frac{2}{3}\end{array}\right) \Gamma \left(\begin{array}{c}-\frac{1}{3}\\\frac{2}{3}\end{array}\right)\)
\(=-\frac{1}{3} \times \frac{2}{3} -\frac{2}{3} \times (-\frac{1}{3})\)
\(=\frac{-2}{9} +\frac{2}{9}=0\)
donc les vecteurs \(\vec{ED}\) et \(\vec{EI}\) sont colinéaires
et donc les points E,D et I sont alignés.
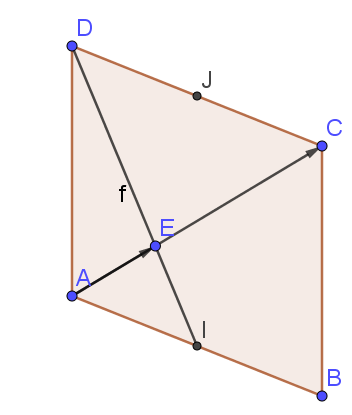
Question
4. a. Déterminer une équation cartésienne de la droite (BJ).
Solution
\(\vec{BJ}=\left(\begin{array}{c}x_J-x_B\\y_J-y_B\end{array}\right)\)
\(\iff \vec{BJ}=\left(\begin{array}{c}\frac{1}{2}-1\\1-0\end{array}\right)\)
\(\iff \vec{BJ}=\left(\begin{array}{c}-\frac{1}{2}\\1\end{array}\right)\)
Soit \(M(x,y)\) un point de la droite (BJ).
Les vecteurs \(\vec{BJ}\) et \(\vec{BM}\) sont colinéaires
donc \(\vec{BJ} \Gamma \vec{BM}=0\)
\(\vec{BM}=\left(\begin{array}{c}x-x_B\\y-y_B\end{array}\right)\)
\(\iff \vec{BM}=\left(\begin{array}{c}x-1\\y-0\end{array}\right)\)
\(\iff \vec{BM}=\left(\begin{array}{c}x-1\\y\end{array}\right)\)
\(\vec{BJ} \gamma \vec{BM}\)
\(=\left(\begin{array}{c}-\frac{1}{2}\\1\end{array}\right)\Gamma \left(\begin{array}{c}x-1\\y\end{array}\right)\)
\(\iff -\frac{1}{2}y-(x-1)=0\)
\(\iff y+2(x-1)=0\)
\(\iff y+2x-2=0\)
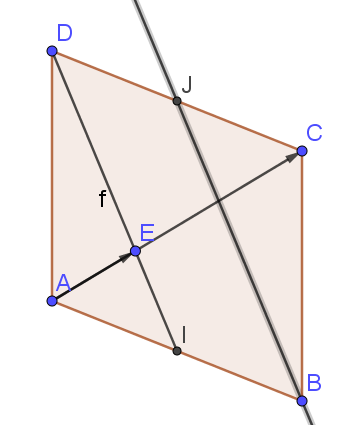
Question
b. Montrer que les droites (BJ) et (ID) sont parallèles.
Solution
\(\vec{ID}=\left(\begin{array}{c}x_D-x_I\\y_D-y_I\end{array}\right)\)
\(\iff \vec{ID}=\left(\begin{array}{c}-\frac{1}{2}\\1\end{array}\right)\)
D'après la question précédente :
\(\vec{BJ}=\left(\begin{array}{c}-\frac{1}{2}\\1\end{array}\right)\)
donc \(\vec{ID}=\vec{BJ}\)
finalement les deux droites (ID) et (BJ) ont un même vecteur directeur
donc ces deux droites sont parallèles.
Question
5. Montrer qu'une équation cartésienne de la droite (AC) est \(x-y=0.\)
Solution
\(\vec{AC}=\left(\begin{array}{c}x_C-x_A\\y_C-y_A\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}1-0\\1-0\end{array}\right)\)
\(\iff \vec{AC}=\left(\begin{array}{c}1\\1\end{array}\right)\)
Soit \(M(x,y)\) un point de la droite (AC).
Les vecteurs \(\vec{AC}\) et \(\vec{AM}\) sont colinéaires
donc \(\vec{AC} \Gamma \vec{AM}=0\)
\(\vec{AM}=\left(\begin{array}{c}x-x_A\\y-y_A\end{array}\right)\)
\(\iff \vec{AM}=\left(\begin{array}{c}x\\y\end{array}\right)\)
\(\vec{AC} \gamma \vec{AM}\)
\(=\left(\begin{array}{c}1\\1\end{array}\right) \gamma \left(\begin{array}{c}x\\y\end{array}\right)=0\)
\(\iff x-y=0\)
Question
6. a. Soit F le point d'intersection des droites (BJ) et (AC).
Calculer les coordonnées de F.
Indication : Résoudre un système de deux équations.
Solution
\(F=(BJ) \cap (AC)\)
\(\iff \begin{cases}y_F+2x_F-2=0\\x_F-y_F=0\end{cases}\)
\(\iff \begin{cases}y_F+2x_F-2=0\\y_F=x_F\end{cases}\)
\(\iff \begin{cases}x_F+2x_F-2=0\\y_F=x_F\end{cases}\)
\(\iff \begin{cases}3x_F-2=0\\y_F=x_F\end{cases}\)
\(\iff \begin{cases}3x_F=2\\y_F=x_F\end{cases}\)
\(\iff \begin{cases}x_F=\frac{2}{3}\\y_F=x_F\end{cases}\)
\(\iff \begin{cases}x_F=\frac{2}{3}\\y_F=\frac{2}{3}\end{cases}\)
Question
b. Prouver que F est le milieu de [EC]
Solution
Calcul des coordonnées du milieu de [EC] :
\(\begin{cases}x=\frac{x_E+x_C}{2}\\y=\frac{y_E+y_C}{2}\end{cases}\)
\(\iff \begin{cases}x=\frac{\frac{1}{3}+1}{2}\\y=\frac{\frac{1}{3}+1}{2}\end{cases}\)
\(\iff \begin{cases}x=\frac{\frac{1}{3}+\frac{3}{3}}{2}\\y=\frac{\frac{1}{3}+\frac{3}{3}}{2}\end{cases}\)
\(\iff \begin{cases}x=\frac{\frac{4}{3}}{2}\\y=\frac{\frac{4}{3}}{2}\end{cases}\)
\(\iff \begin{cases}x=\frac{2}{3}\\y=\frac{2}{3}\end{cases}\)
On retrouve les coordonnées du point F
donc F est le milieu du segment [EC]