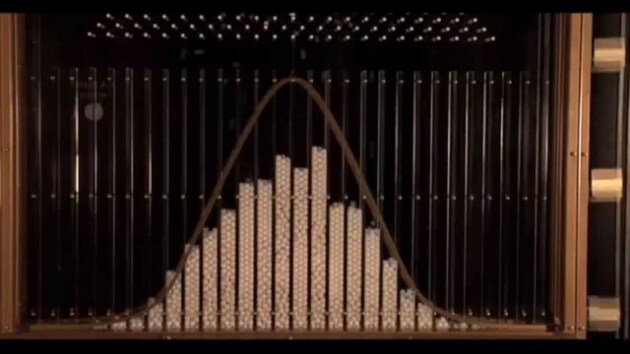
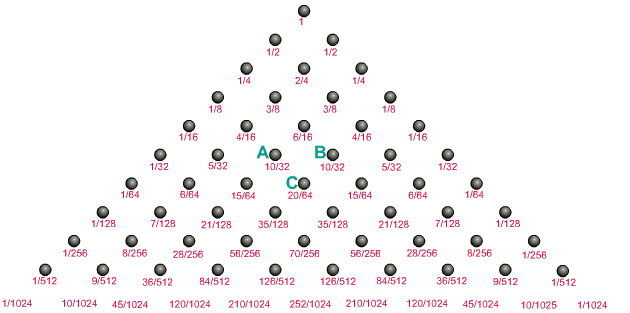
Planche Galton
Fondamental :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Sir Francis Galton (16 février 1822 - 17 janvier 1911) statisticien britannique.
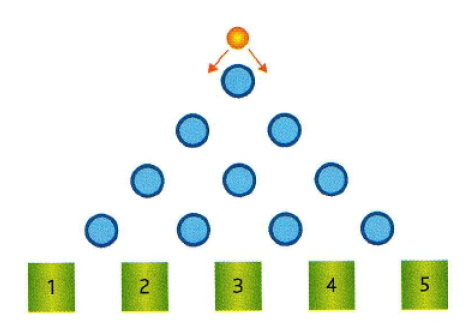
Soit X la variable aléatoire qui a un lancer de la bille associe le numéro de la case où elle est tombée à la fin de son parcours.
1.Déterminer la loi de probabilité de la variable aléatoire X
2. Déterminer le score que l'on peut espérer obtenir lors d'un grand nombre de lancers.
3.Calculer la variance et l'écart type de la variable aléatoire X.Interpréter ces résultats.
Complément :
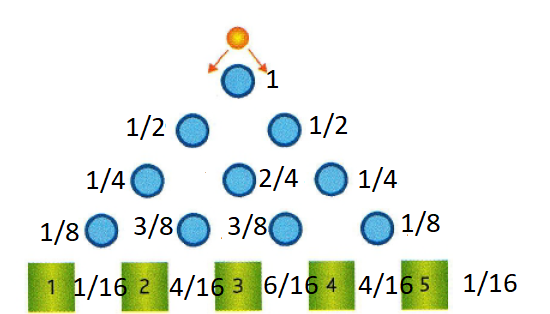
\(x_i\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{1}{16}\) | \(\frac{4}{16}=\frac{1}{4}\) | \(\frac{6}{16}=\frac{3}{8}\) | \(\frac{4}{16}=\frac{1}{4}\) | \(\frac{1}{16}\) |
\(E(X)=\frac{1}{16}\times 1+\frac{4}{16} \times 2 +\frac{6}{16} \times 3 +\frac{4}{16} \times 4+ \frac{1}{16} \times 5\)
\(=\frac{1}{16}+\frac{8}{16} +\frac{18}{16} +\frac{16}{16} + \frac{5}{16}\)
\(=\frac{48}{16}=3\)
donc \(\color{red}{\textbf{Sur un grand nombre de parties, on peut espérer en moyenne obtenir le score de 3 points.}}\)
\(V(X)=\frac{1}{16}\times (1-3)^2+\frac{4}{16} \times (2-3)^2 +\frac{6}{16} \times (3-3)^2 +\frac{4}{16} \times (4-3)^2+ \frac{1}{16} \times (5-3)^2\)
\(V(X)=\frac{1}{16}\times 4+\frac{4}{16} \times 1+\frac{6}{16} \times 0 +\frac{4}{16} \times 1+ \frac{1}{16} \times 4\)
\(V(X)=\frac{4}{16}+\frac{4}{16} +\frac{4}{16} + \frac{4}{16}=1\)
\(\sigma(X)=\sqrt{V(X)}=\sqrt{1}=1\)
donc \([E(X)-\sigma(X);E(X)+\sigma(X)]=[3-1 ;3+1]=[2 ;4]\)
\(\color{red}{\textbf{On peut donc espérer obtenir sur un grand nombre de parties avec une forte chance un résultat entre 2 et 4.}}\)
\(\color{red}{\textbf{Les cases 1 et 5 ont une probabilité très faible d'être obtenue.}}\)