Exercice : Alice au Pays des Merveilles
Alice, de Alice au Pays des Merveilles, prend le thé une fois par jour.
Soit \(N\) la variable aléatoire qui, à chaque jour,
associe le nombre de personnes buvant le thé avec elle.
La loi de probabilités de la variable aléatoire \(N\) est :
\(n_i\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
\(p(N = x_i)\) | 0,15 | 0,28 | 0,2 | 0,2 | \(a\) |

Question
1. Déterminer la valeur de \(a\)
Solution
La somme des probabilités de toutes les issues doit être égale à 1 :
\(P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)=1\)
\(\iff 0,15+0,28+0,2+0,2+P(X=5)=1\)
\(\iff P(X=5)=1−0,83=0,17\)
\(\iff a=P(X=5)=0,17\)
La probabilité que le nombre de personnes buvant le thé avec Alice est 0,17
Question
2. Calculer la probabilité que deux amis au moins prennent le thé avec Alice
Solution
La probabilité que deux amis au moins prennent le thé avec Alice signifie qu'on recherche la probabilité de l'évènement \("X≥2"\).
\(P(X≥2)=P(X=2)+P(X=3)+P(X=4)+P(X=5)=0,28+0,2+0,2+0,17=0,85\)
ou
\(P(X≥2)=P( \overline{X=1})=1-P(X=1)=1-0,15=0,85\)
La probabilité que deux amis au moins prennent le thé avec Alice est 0,85
soit 85% de chance que deux amis au moins prennent le thé avec Alice.
Question
3. Calculer la probabilité que moins de 5 amis prennent le thé avec Alice
Solution
La probabilité que moins de 5 amis prennent le thé avec Alice signifie qu'on recherche la probabilité de l'évènement \("X<5"\) :
\(P(X<5)=P(X≤4)=P(X=1)+P(X=2)+P(X=3)+P(X=4)=0,15+0,28+0,2+0,2=0,83\)
ou
\(P(X<5)=P(\overline{X=5})=1-P(X=5)=1-0,17=0,83\)
donc \(P(X<5)=0,83\)
La probabilité que moins de 5 amis prennent le thé avec Alice est 0,83
soit 83% de chance que moins de 5 amis prennent le thé avec Alice.
Question
4. Calculer \(p(2 \le X \le 4)\) et interpréter le résultat par une phrase.
Solution
Pour calculer \(P(2≤X≤4)\), nous devons additionner les probabilités que la variable aléatoire \(X\) prenne les valeurs 2, 3 et 4.
\(P(2≤X≤4)=P(X=2)+P(X=3)+P(X=4)=0,28+0,20+0,20=0,68\)
ou
\(P(2≤X≤4)=P(X≤4)-P(X < 2)=P(X<5)-P(X=1)\)
\(\iff P(2≤X≤4)=0,85-0,15\)
\(\iff P(2≤X≤4)=0,68\)
La probabilité qu'Alice prenne le thé avec entre 2 et 4 amis inclus un jour donné est de 0,68 donc il y a 68 % de chances qu'Alice partage son thé avec 2, 3 ou 4 personnes un jour donné.
Complément :
L'espérance est donnée par :
\(E(X)=∑x_iP(X=x_i)=1×0,15+2×0,28+3×0,2+4×0,2+5×0,17=0,15+0,56+0,6+0,8+0,85=2,96\)
En moyenne, Alice prend le thé avec environ 3 personnes par jour.
La variance est donnée par :
\(V(X)=E(X^2)−[E(X)]^2\)
\(E(X^2)=∑x_i^2P(X=x_i)=1^2×0,15+2^2×0,28+3^2×0,20+4^2×0,20+5^2×0,17\)
\(\iff E(X^2)=0,15+1,12+1,80+3,20+4,25=10,52\)
\(\Rightarrow V(X)=10,52−(2,96)2=10,52−8,7616=1,7584\)
\(\Rightarrow σ(X)=\sqrt{V(X)}=\sqrt{1,7584}≈1,326\)
\(\Rightarrow [E(X)−σ(X);E(X)+σ(X)]≈[2,96−1,326;2,96+1,326]≈[1,634;4,286]\)
Environ 68 % des jours, le nombre de personnes prenant le thé avec Alice se situe entre 1,63 et 4,29.
Comme la variable aléatoire \(X\)X est une variable aléatoire prenant des valeurs entières (discrète), on peut interpréter cet intervalle comme couvrant principalement les valeurs \(X=2\), \(X=3\) et \(X=4\)
Cela correspond bien à la probabilité \(P(2≤X≤4)=0,68\) calculée précédemment.

Le Lièvre de Mars qui court toujours après le temps organise un jeu à la fin du goûter selon les règles suivantes :
Il place 3 tasses à thé de couleurs différentes sur la table et il cache sous l'une d'elle une montre brisée indiquant perpétuellement l’heure du thé.
Le joueur doit miser « 6 minutes de temps »
Si le joueur trouve la montre au premier essai , il gagne « 10 minutes de temps ».
Si le joueur trouve la montre au deuxième essai, sa mise lui est rendue.
Si le joueur trouve la montre au troisième essai, il perd sa mise.
On définit la variable aléatoire \(T\) qui, à chaque partie, associe le «gain» algébrique du joueur (ce « gain » est négatif si le joueur perd du temps)
Question
1.Compléter l'arbre de probabilité avec les probabilités de trouver la montre au premier, deuxième essai ou au deuxième essai
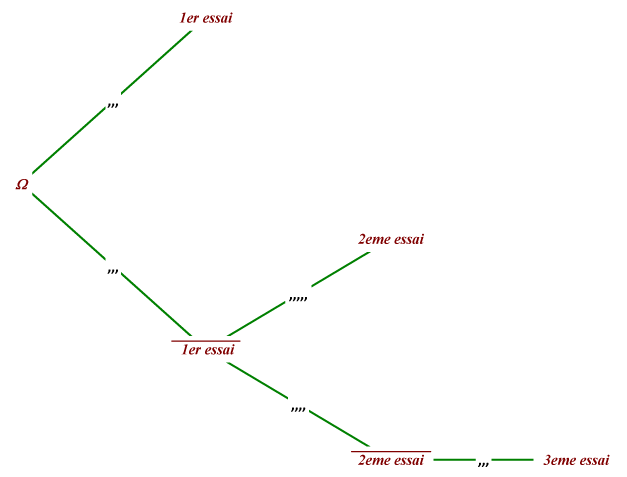
Solution
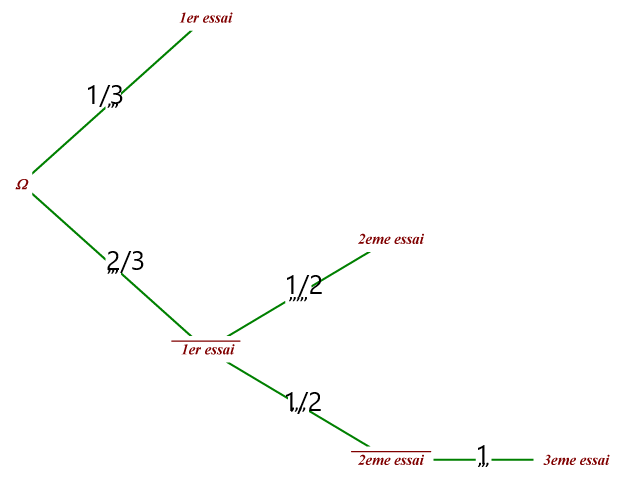
Au premier essai :
la probabilité de trouver la montre est \(\frac{1}{3}\)
la probabilité de ne pas trouver la montre est \(1-\frac{1}{3}=\frac{2}{3}\)
car la montre est seulement sous une des 3 tasses.
Si premier essai est un échec,
la probabilité de trouver la montre au deuxième essai est \(\frac{1}{2}\)
la probabilité de ne pas trouver la montre au deuxième essai est \(1-\frac{1}{2}=\frac{1}{2}\)
car la montre est seulement sous une des 2 tasses restantes.
Si deuxième essai échoue,
la probabilité de trouver la montre au 3ème et dernier essai est \(1\)
la montre se trouve forcément sous la dernière tasse.
Question
2. Montrer que la loi de probabilité de la variable aléatoire \(T\) est :
Temps \(t_i\) | -6 | 0 | 4 |
|---|---|---|---|
\(p(T=t_i)\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) |
Solution
Le gain si la montre est trouvée au premier essai est: 10−6=4 minutes
\(P(T=4)=\frac{1}{3}\)
Le gain si la montre est trouvée au deuxième essai est: 0 minute car la mise est rendue au joueur.
\(P(T=0)=\frac{2}{3}×\frac{1}{2}=\frac{1}{3}\)
Le gain si la montre est trouvée au troisième essai est: −6 minutes car la mise est perdue
\(P(T=−6)=\frac{2}{3}×\frac{1}{2} ×1=\frac{1}{3}\)
Question
3. Calculer l'espérance mathématique \(E(T)\) et interpréter son résultat.
Solution
\(E(T)=4×\frac{1}{3}+0×\frac{1}{3}+(−6)×\frac{1}{3}=-\frac{2}{3}\)
En moyenne, le joueur perd -\(\frac{2}{3}\) minute soit environ 0,67 minute par partie.
Question
4. Analyser le risque pour le joueur par le calcul de la variance et de l'écart-type.
Solution
Temps \(t_i^2\) | 36 | 0 | 16 |
|---|---|---|---|
\(p(T^2=t_i^2)\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) |
\(E(T^2)=16×\frac{1}{3}+0×\frac{1}{3}+36×\frac{1}{3}=\frac{52}{3}\)
\(V(T)=E(T^2)−[E(T)]2=\frac{52}{3}−(−\frac{2}{3})2=\frac{52}{3}−\frac{4}{9}\)
\(\iff V(T)=\frac{156}{9}−\frac{4}{9}=\frac{152}{9}\)
\(σ(T)=\sqrt{\frac{152}{9}}=\frac{\sqrt{152}}{3}≈4,11\)
Le risque est élevé car l'écart-type est grand par rapport à l'espérance.
L'intervalle de confiance est :
\([E(T)-σ(T);E(T)+σ(T)]=[-\frac{2}{3}-\frac{\sqrt{152}}{3} ;-\frac{2}{3}+\frac{\sqrt{152}}{3}]\)
\(\iff [E(T)-σ(T);E(T)+σ(T)]=[-0,67-4,11 ;-0,67+4,11]\)
\(\iff [E(T)-σ(T);E(T)+σ(T)]=[-4,78 ;3,44]\)
Environ 68 % du temps, le gain algébrique du joueur sera compris entre -4,78 minutes et +3,44 minutes.

Les masses des sachets de thé servis par le Chapelier Fou varient autour de 1 g par bonds de 0,01 g, selon la loi de probabilité suivante :
Loi de probabilité de la variable aléatoire masses des sachets de thé :
Masse \(m_i\) | 0,994 | 0,996 | 0,999 | 1 | 1,003 | 1,005 | 1,007 |
|---|---|---|---|---|---|---|---|
\(p(M=m_i)\) | 0,05 | 0,10 | 0,05 | 0,25 | 0,25 | 0,20 | 0,10 |
Question
Compléter la loi de probabilité de la variable aléatoire \(N=1000M-1000\)
\(n_i\) | |||||||
|---|---|---|---|---|---|---|---|
\(p(N=n_i)\) |
Solution
La variable aléatoire N représente l'écart en milligrammes (mg) par rapport à la masse nominale de 1000 mg (1 g).
Exemple :
N=−6 signifie que le sachet pèse 6 mg de moins que 1 g.
N=7 signifie qu'il pèse 7 mg de plus que 1 g.
La loi de probabilité de la variable aléatoire N est :
\(n_i\) | -6 | -4 | -1 | 0 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|
\(p(N=n_i)\) | 0,05 | 0,10 | 0,05 | 0,25 | 0,25 | 0,20 | 0,10 |
Remarque :
Cette transformation permet de travailler avec des entiers (écarts en mg) plutôt qu'avec des décimaux (masse en g).
Elle est utile pour simplifier les calculs statistiques ultérieurs (espérance, variance)
Question
2. Calculer l'espérance \(E(N)\) en déduire l'espérance \(E(M)\) de la masse d’un sachet de thé.
Solution
La variable aléatoire \(N=1000M−1000\) est une transformation linéaire de la variable aléatoire \(M\).
\(E(N)=∑n_i⋅P(N=n_i)\)
\(\Rightarrow E(N)=(−6)×0,05+(−4)×0,10+(−1)×0,05+0×0,25+3×0,25+5×0,20+7×0,10\)
\(\iff E(N)=−0,3−0,4−0,05+0+0,75+1,0+0,7=1,7 mg\)
En utilisant la linéarité de l'espérance :
\(E(N)=E(1000M−1000)=1000E(M)−1000=1,7\)
\(\iff 1000E(M)=1001,7\)
\(\iff E(M)=\frac{1001,7}{1000}\)
\(\iff E(M)=1,0017 g\)
La masse moyenne d'un sachet de thé est donc de 1,0017 g
Question
3. Calculer la variance \(V(N)\) en déduire la variance \(V(M)\) de la masse d’un sachet de thé.
Solution
La variance de variable aléatoire \(N\) est donnée par :
\(V(N)=E(N^2)−[E(N)]^2\)
\(E(N^2)=∑n_i^2⋅P(N=ni)\)
\(E(N^2)=(−6)^2×0,05+(−4)^2×0,10+(−1)^2×0,05+0^2×0,25+3^2×0,25+5^2×0,20+7^2×0,10\)
\(\iff E(N^2)=36×0,05+16×0,10+1×0,05+0×0,25+9×0,25+25×0,20+49×0,10\)
\(\Rightarrow V(N)=E(N^2)−[E(N)]^2=15,6−(1,7)^2=15,6−2,89=12,71 mg^2\)
Par transformation linéaire :
Comme \(N=1000M−1000\) la variance de la variable aléatoire \(N\) est liée à celle de M par :
\(V(N)=V(1000M−1000)=1000^2⋅V(M)\)
\(\iff 12,71=1000^2⋅V(M)\)
\(\iff 1000^2⋅V(M)=12,71\)
\(\iff V(M)=\frac{12,71}{1000^2}\)
\(\iff V(M)=\frac{12,71}{(10^3)^2}\)
\(\iff V(M)=\frac{12,71}{10^6}\)
\(\iff V(M)=12,71 \times 10^{-6}\)
\(\iff V(M)=1,271 \times 10^{-5}\)
\(σ(M)=\sqrt{V(M)}=\sqrt{1,271 \times 10^{-5}}≈0,00356\)
Calcul de l'intervalle de confiance :
\([E(M)-σ(M);E(M)+σ(M)]≈[1,0017−0,00356 ; 1,0017+0,00356]≈[0,9981 ; 1,0053]\)
Environ 68 % des sachets ont une masse comprise entre 0,9981 g et 1,0053 g.
La masse nominale étant de 1 g, l'intervalle montre que :
La majorité des sachets sont conformes (très proches de 1 g).
Quelques sachets peuvent être légèrement sous-dosés (jusqu'à 1,9 mg en moins) ou surdosés (jusqu'à 5,3 mg en plus).
L'écart-type très faible indique une production très précise.
L'intervalle est asymétrique autour de 1 g, car \(E(M)=1,0017\) (léger surdosage systématique).