Méthode de Monté Carlo - Geogebra
Fondamental :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
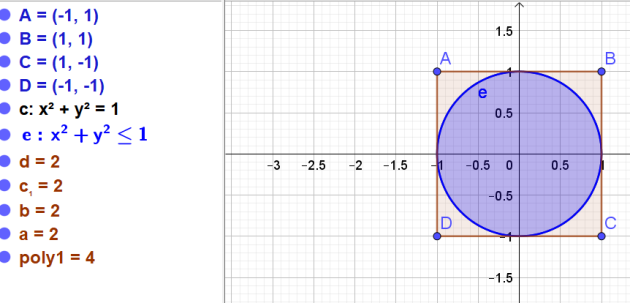
1) Construction de la « cible »
Créer les différents objets mathématiques ci-dessous.
On construit :
le carré ABCD de coté 2.
le cercle de centre O et de rayon 1.
L'équation du disque de centre O et de rayon 1 est donc \(x^2+y^2=1\)
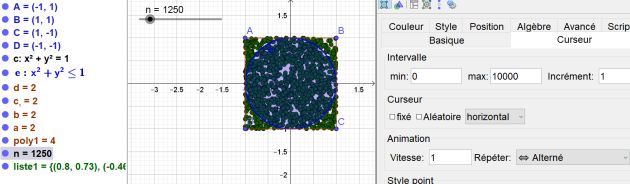
2) Lancer des « fléchettes » (les points de simulation)
« liste1=Séquence[(AléaUniforme[-1,1],AléaUniforme[-1,1]),i,1,n] »
On place un point de coordonnées \((x;y)\) \(x\) et \(y\) choisis aléatoirement entre -1 et 1.
En réitérant ce lancer un nombre de fois très grand, on peut arriver à recouvrir le quart de disque.
3) Déterminer si les « fléchettes » sont tombées dans la zone utile.
« liste2=Séquence[EstDansRégion[Elément[liste1,i],c],i,1,n] »
4) Compter le nombre de « fléchettes » qui sont tombées dans la zone utile.
« Somme[liste2] »
\(\textbf{Aire du carré :} côté^2=2^2=4\)
\(\textbf{Aire du disque :} \pi \times rayon^2=\pi \times 1^2=\pi\)
\(\frac{\textbf{Aire du disque}}{\textbf{Aire du carré}}=\frac{\pi}{\textbf{4}}\)
Le quotient du nombre de points par le nombre de lancers est une approximation de \(\frac{\pi}{\textbf{4}}\).
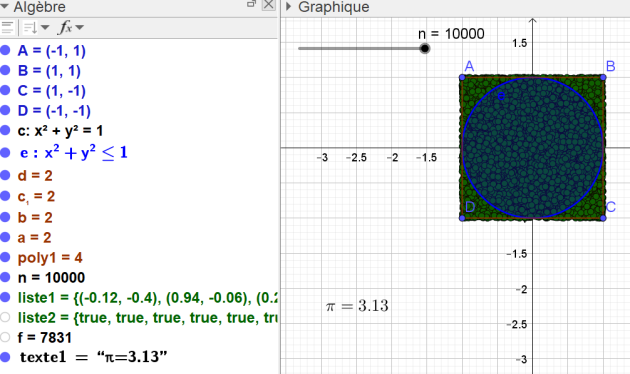
5) Tester l'algorithme pour \(n\)=100 ; \(n\)= 1 000 ; \(n\)=10 000.
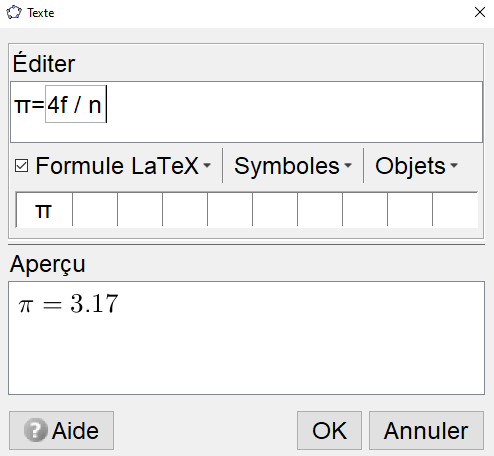
6) Afficher un texte donnant la valeur de π
\(π=\frac{\textbf{Aire du disque}}{\textbf{Aire du carré}}\times 4\)
\(π=\frac{f}{n}\times 4\)
7) A-t-on une approximation convenable de π ?