Exercice : Avec ou sans remise
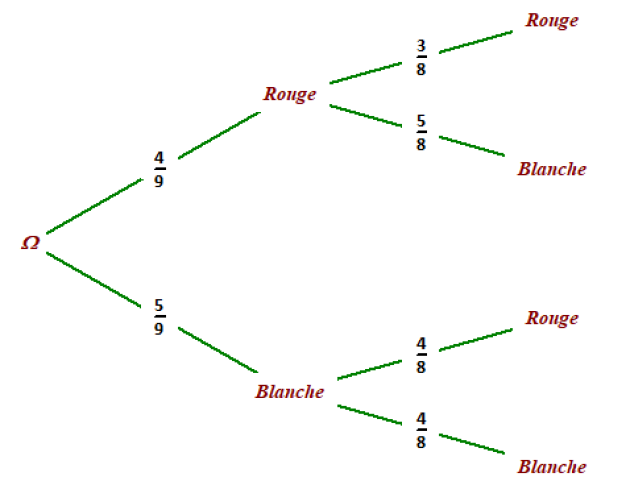
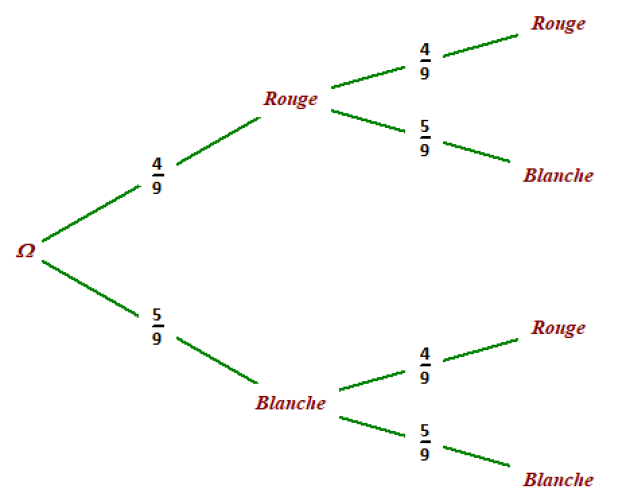
Une urne contient quatre boules rouges et cinq boules blanches indiscernables au toucher.
Un joueur a le choix entre deux jeux.
\(\color{magenta}{\textbf{Jeu n°1 :}}\) Le joueur tire une boule, note sa couleur, puis, sans remettre la première dans l'urne, en tire une seconde dont il note également la couleur.
• Si les deux boules sont de couleurs différentes, le joueur gagne 3€.
• Si les deux boules sont rouges, il perd 2€.
• Si les deux boules sont blanches, il perd 10€.
\(\color{magenta}{\textbf{Jeu n°2 :}}\) Le joueur tire une boule, note sa couleur, la remet dans l'urne puis en tire une seconde dont il note aussi la couleur.
\(\color{red}{\textbf{Les règles concernant les sommes gagnées ou perdues sont les mêmes que pour le jeu n°1.}}\)
\(\color{magenta}{\textbf{On note respectivement X et Y les variables aléatoires donnant le gain algébrique du joueur dans les jeux 1 et 2.}}\)
Question
1. Donner les lois de probabilité de X et de Y et calculer leurs espérances mathématiques.
Solution
\(p("gagner 3€")=p((R,B))+p((B,R))=\frac{4}{9}\times \frac{5}{8}+\frac{5}{9}\times \frac{4}{8}\)
\(\iff p("gagner 3€")=\frac{1}{9}\times \frac{5}{2}+\frac{5}{9}\times \frac{1}{2}\)
\(\iff p("gagner 3€")=\frac{5}{18}+\frac{5}{18}\)
\(\iff p("gagner 3€")=\frac{10}{18}=\frac{5}{9}\)
\(p("perdre 2€")=p((R,R))=\frac{4}{9}\times \frac{3}{8}\)
\(\iff p("perdre 2€")=p((R,R))=\frac{1}{3}\times \frac{1}{2}\)
\(\iff p("perdre 2€")=\frac{1}{6}\)
\(p("perdre 10€")=p((B,B))=\frac{5}{9}\times \frac{4}{8}\)
\(\iff p("perdre 10€")=p((B,B))=\frac{5}{9}\times \frac{1}{2}\)
\(\iff p("perdre 10€")=\frac{5}{18}\)
\(x_i\) | -10 | -2 | 3 |
|---|---|---|---|
\(p(X=x_i)\) | \(\frac{5}{18}\) | \(\frac{1}{6}\) | \(\frac{5}{9}\) |
\(E(X)=\frac{1}{6}\times (-2)+\frac{5}{18}\times (-10)+\frac{5}{9}\times 3\)
\(\iff E(X)=\frac{-1}{3}+\frac{-25}{9}+\frac{5}{3}\)
\(\iff E(X)=\frac{-3}{9}-\frac{25}{9}+\frac{15}{9}\)
\(\iff E(X)=-\frac{13}{9}\)
\(V(X)=\frac{1}{6}\times [(-2)-(-\frac{13}{9})]^2+\frac{5}{18}\times [(-10)-(-\frac{13}{9})]^2+\frac{5}{9}\times [3-(-\frac{13}{9})]^2\)
\(\iff V(X)=\frac{1}{6}\times [-2+\frac{13}{9}]^2+\frac{5}{18}\times [-10+\frac{13}{9}]^2+\frac{5}{9}\times [3+\frac{13}{9}]^2\)
\(\iff V(X)=\frac{1}{6}\times [-\frac{18}{9}+\frac{13}{9}]^2+\frac{5}{18}\times [-\frac{90}{9}+\frac{13}{9}]^2+\frac{5}{9}\times [\frac{27}{9}+\frac{13}{9}]^2\)
\(\iff V(X)=\frac{1}{6}\times (\frac{5}{9})^2+\frac{5}{18}\times (-\frac{77}{9})^2+\frac{5}{9}\times (\frac{40}{9})^2\)
\(\iff V(X)=\frac{1}{6}\times \frac{25}{81}+\frac{5}{18}\times \frac{5929}{81}+\frac{5}{9}\times \frac{1600}{81}\)
\(\iff V(X)=\frac{25}{486}+\frac{29 645}{1458}+\frac{8000}{729}\)
\(\iff V(X)=\frac{75}{1458}+\frac{29 645}{1458}+\frac{16000}{1458}\)
\(\iff V(X)=\frac{45720}{1458}\)
\(\iff V(X)=\frac{22860}{729}\)
\(\iff V(X)=\frac{7620}{243}\)
\(\iff V(X)=\frac{2540}{81}\)
\(\iff V(X)\simeq 31,36\)
\(\sigma(X)=\sqrt{V(X)}\)
\(\iff \sigma(X) \simeq 5,6\)
\([E(X)-\sigma(X) ;E(X)+\sigma(X) ] \simeq [-\frac{13}{9}-5 ,60 ;-\frac{13}{9}+5,60]\)
\(\iff [E(X)-\sigma(X) ;E(X)+\sigma(X) ] \simeq [-7,04,24 ;4,4]\)
\(p("gagner 3€")=p((R,B))+p((B,R))=\frac{4}{9}\times \frac{5}{9}+\frac{5}{9}\times \frac{4}{9}\)
\(\iff p("gagner 3€")=\frac{20}{81}+\frac{20}{81}\)
\(\iff p("gagner 3€")=\frac{40}{81}\)
\(p("perdre 2€")=p((R,R))=\frac{4}{9}\times \frac{4}{9}\)
\(\iff p("perdre 2€")=p((R,R))=\frac{16}{81}\)
\(p("perdre 10€")=p((B,B))=\frac{5}{9}\times \frac{5}{9}\)
\(\iff p("perdre 10€")=p((B,B))=\frac{25}{81}\)
\(y_i\) | -10 | -2 | 3 |
|---|---|---|---|
\(p(Y=y_i)\) | \(\frac{25}{81}\) | \(\frac{16}{81}\) | \(\frac{40}{81}\) |
\(E(Y)=\frac{25}{81}\times (-10)+\frac{16}{81}\times (-2)+\frac{40}{81}\times 3\)
\(\iff E(Y)=\frac{-250}{81}-\frac{32}{81}+\frac{120}{81}\)
\(\iff E(Y)=\frac{-282}{81}+\frac{120}{81}\)
\(\iff E(Y)=-\frac{-162}{81}=-2=-\frac{18}{9}\)
\(V(Y)=\frac{16}{81}\times [(-2)-(-2)]^2+\frac{25}{81}\times [(-10)-(-2)]^2+\frac{40}{81}\times [3-(-2)]^2\)
\(\iff V(Y)=\frac{16}{81}\times [-2+2]^2+\frac{25}{81}\times [-10+2]^2+\frac{40}{81}\times [3+2]^2\)
\(\iff V(Y)=\frac{16}{81}\times 0^2+\frac{25}{81}\times (-8)^2+\frac{40}{81}\times 5^2\)
\(\iff V(Y)=\frac{25}{81}\times 64+\frac{40}{81}\times 25\)
\(\iff V(Y)=\frac{1600}{81}+\frac{1000}{81}\)
\(\iff V(Y)=\frac{2600}{81}\)
\(\sigma(Y)=\sqrt{V(Y)}\)
\(\iff \sigma(Y)=\sqrt{\frac{2600}{81}}\)
\(\iff \sigma(Y)=\sqrt{\frac{2600}{81}}\)
\(\iff \sigma(Y)=\frac{10\sqrt{26}}{9}\)
\(\iff \sigma(Y)\simeq 5,66\)
\([E(Y)-\sigma(Y) ;E(Y)+\sigma(Y) ] \simeq [-2-5,66 ;-2+5,66]\)
\(\iff [E(Y)-\sigma(Y) ;E(Y)+\sigma(Y) ] \simeq [-7,66 ;3,66]\)
Question
2. Quel est le jeu le plus avantageux pour le joueur ?
Solution
Le jeu le moins désavantageux est le jeu 1 car l'espérance de gain du joueur
est supérieure à celle du jeu 2 mais les deux espérances sont négatives
donc les deux jeux sont en moyenne sur un grand nombre de parties défavorable au joueur
mais le jeu 1 est moins désavantageux.
L'intervalle des gains pour le jeu 1 est également inclus dans l'intervalle des gains du jeu 2.
\([E(X)-\sigma(X) ;E(X)+\sigma(X) ] \subset [E(Y)-\sigma(Y) ;E(Y)+\sigma(Y) ]\)
car \([-7,04,24 ;4,4] \subset [-7,66 ;3,66]\)