CHAPITRE VIII : Les probabilités sur un ensemble fini
Exemple :
\(\color{red}{\text{Problème Vidéo Monopoly}}\)
En 1654, Blaise Pascal (1623 ; 1662) entretient avec Pierre de Fermat (1601 ; 1665) des correspondances sur le thème des jeux de hasard et d'espérance de gain qui les mènent à exposer une théorie nouvelle :
les calculs de probabilités.
Ils s'intéressent à la résolution de problèmes de dénombrement comme par exemple celui du Chevalier de Méré :
« Comment distribuer équitablement la mise à un jeu de hasard interrompu avant la fin de la partie ? »

On attribue l'origine du mot hasard à l'arabe « al-zahr » signifiant à l'origine « dés » et ayant pris la signification de « chance », car il désigna jusqu'au XII e siècle un jeu de dés, mais aussi tous les domaines relevant de la « science de la Chance ».
Définition : I. Définition
\(\color{red}{\textbf{Une expérience est aléatoire lorsqu'elle a plusieurs résultats ou issues possibles (toutes connues) }}\)
\(\color{red}{\textbf{et que l'on ne peut pas prévoir, ni calculer, à priori, quel résultat se produira.}}\)
\(\color{red}{\textbf{Le résultat est le fruit du hasard.}}\)
\(\color{red}{\textbf{L'ensemble des issues d'une expérience s'appelle l'univers Ω.}}\)
\(\color{red}{\textbf{On appelle événement un ensemble d'issues d'une expérience aléatoire.}}\)
\(\color{red}{\textbf{La probabilité d'un événement est par définition la somme des probabilités des issues qui le composent.}}\)
Complément :
Lancer d'une pièce de monnaie : L'univers Ω = {pile ;face} ce sont les issues possibles.
Lancer un dé à six faces : L'univers Ω = {1; 2; 3; 4; 5; 6} ce sont les issues possibles.
Événement impossible obtenir un 7.
Exemple :
\(\color{magenta}{\text{ Exercice Monopoly}}\)
Complément :
On attribue l'origine du mot hasard à l'arabe « al-zahr » signifiant à l'origine « dés » et ayant pris la signification de « chance »,
car il désigna jusqu'au XII e siècle un jeu de dés, mais aussi tous les domaines relevant de la « science de la Chance ».
Exemple :
\(\color{magenta}{\text{Exemples 1 à 4}}\)
II. Probabilité d'un événement
.
Exemple : 1. Arbre des possibles
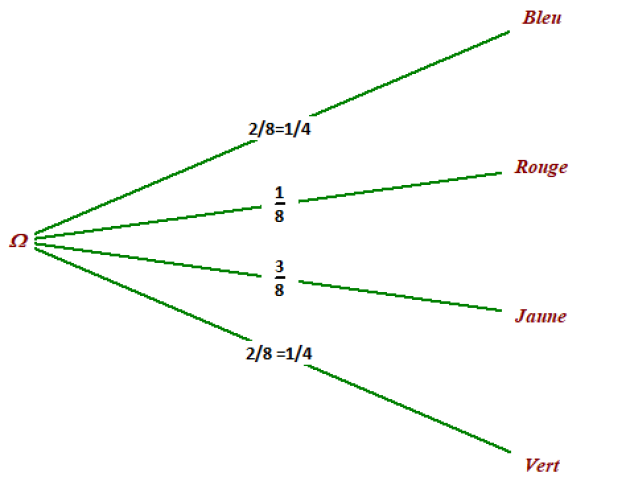
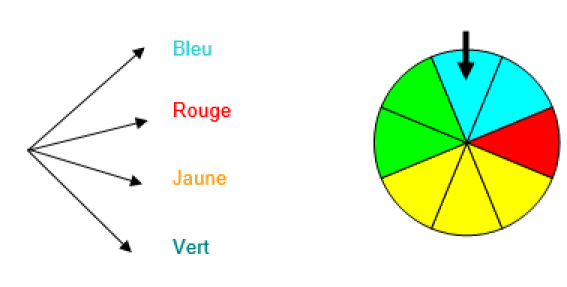
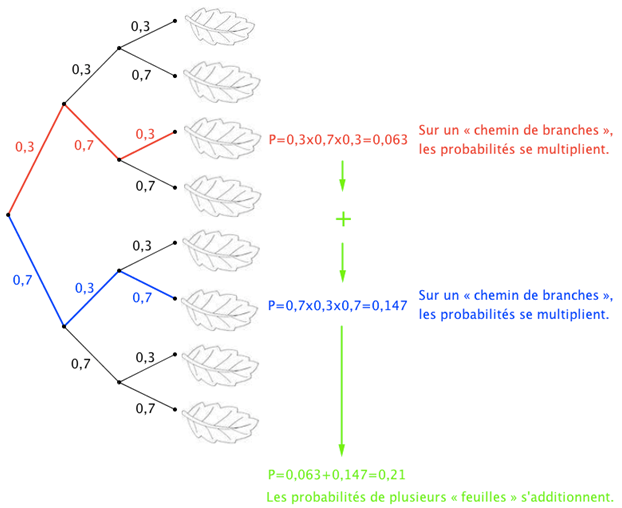
Lorsqu'on fait tourner la roue, quatre issues sont possibles. On le schématise sur l'arbre des possibles :
Exemple :
2 secteurs sur 8 sont de couleur bleue. Lors d'une expérience aléatoire, il y a donc 2 chances sur 8 d'obtenir un secteur de couleur bleue.
On dit que la probabilité d'obtenir un secteur bleu est égale à , \(\frac{2}{8}\) soit \(\frac{1}{4}\).
On inscrit sur l'arbre des possibles les probabilités des différentes issues.
Définition :
\(\color{red}{\textbf{L'arbre des possibles permet de visualiser les issues d'une expérience aléatoire.}}\)
Définition : 2. Probabilité
Déterminer la probabilité de l’événement\( \color{magenta}{\textbf{E "La roue s'arrête sur un secteur bleu ou rouge"}}\),
Exemple :
Soit l’événement\( \color{magenta}{\textbf{E "La roue s'arrête sur un secteur bleu ou rouge"}}\),
p(E) = p("La roue s'arrête sur un secteur bleu")+p("La roue s'arrête sur un secteur rouge")
\(\iff p(E) = \frac{1}{4}+\frac{1}{8}\)
\(\iff p(E) = \frac{2}{8}+\frac{1}{8}\)
\(\iff p(E) = \frac{3}{8}\)
Exemple :
\(\color{magenta}{\text{Exercice Digicode}}\)
Exemple :
\(\color{magenta}{\textbf{E : "« La roue s'arrête sur un secteur bleu ou rouge »"}}\) E est un \(\color{red}{\textbf{événement.}}\)
\(\color{magenta}{\textbf{F : « La roue s'arrête sur un secteur bleu »}}\) ou \(\color{magenta}{\textbf{G : « La roue s'arrête sur un secteur rouge »}}\)
F et G sont des \(\color{red}{\textbf{événements élémentaires.}}\)
Définition :
\(\color{red}{\textbf{Lorsqu'on associe à toutes les issues la même probabilité, }}\)
\(\color{red}{\textbf{ on parle d'équiprobabilité sur l'expérience aléatoire.}}\)
Remarque :
\(\color{magenta}{\textbf{Dans le cas d'équiprobabilité,}}\)
\(\color{magenta}{\textbf{s'il y a n issues à l'expérience alors chaque issue a pour probabilité :}}\)
\(\color{magenta}{\frac{1}{n}}\)
Exemple :
\(\color{magenta}{\text{Exemples 5 à 11}}\)
Fondamental : Propriétés :
\(\color{red}{\textbf{La probabilité P(E) d'un événement E est telle : 0 ≤ P(E) ≤ 1.}}\)
\(\color{red}{\textbf{Une probabilité nulle correspond à l'événement } \underline{impossible } \varnothing}\)
\(\color{red}{\textbf{Une probabilité de un correspond à l'événement } \underline{certain} \Omega. }\)
\(\color{red}{\textbf{La somme des probabilités des événements élémentaires est égale à 1.}}\)
\(\color{red}{\textbf{La probabilité d'un événement est la somme des probabilités des événements élémentaires qui le constituent.}}\)
\(\color{red}{\textbf{La probabilité de l'événement contraire d'un événement E est : }}\)\(\color{red}{p(\overline{E}) = 1 – p(E)}\)
Définition : III. Réunion et intersection de deux événements
\(\color{red}{\textbf{L'événement "A et B", noté } A \cap B \textbf{ (intersection), est réalisé lorsque les deux événements A et B sont simultanément réalisés.}}\)
\(\color{red}{\textbf{L'événement "A ou B", noté } A\cup B \textbf{(réunion), est réalisé lorsqu'au moins l'un des deux événements est réalisé.}}\)
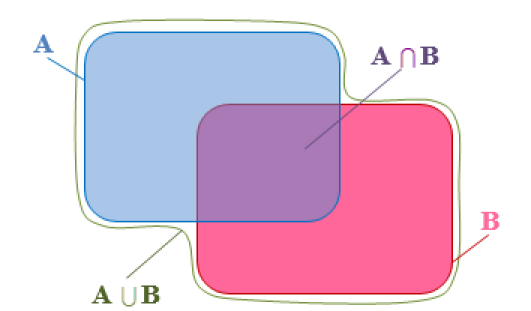
Remarque :
Exemple :
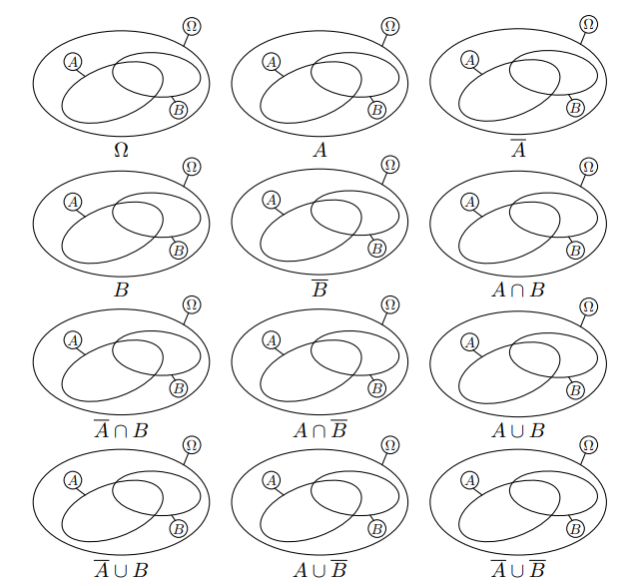
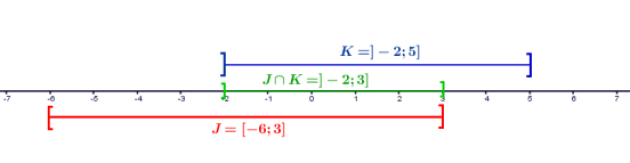
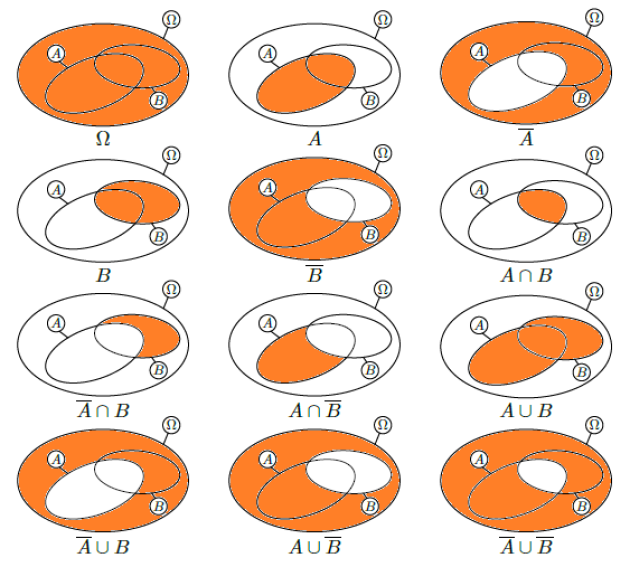
Ci-dessus sont représentés l'univers Ω d'une expérience aléatoire et deux événements A et B de Ω.
Pour chacune des représentations ci-dessous, hachurer l'ensemble demandé.
Complément :
Définition : 2) Probabilité d'une réunion
\(\color{red}{\textbf{Si A et B sont deux événements d'une expérience aléatoire, alors :}}\)
\(\color{red}{p(A \cup B)=p(A)+p(B)-p(A \cap B)}\)
Définition : 3) Evénements incompatibles
\(\color{red}{\textbf{On dit que deux événements A et B sont incompatibles si }}A \cap B =\varnothing .\)
Exemple :
Lors d'un lancé à 6 faces, l'évènement A"obtenir un nombre pair" et B "obtenir un nombre 3" sont incompatibles.
Aucune issue ne réalise à la fois A et B donc \(\color{red}{A \cap B= \varnothing}\)
Fondamental : Propriété :
\(\color{red}{\textbf{Si deux événements A et B sont incompatibles alors }P(A\cup B)=P(A)+P(B)}\)
Complément :
\(p(A)=p("obtenir les nombres 2,4,6")=\frac{3}{6}=\frac{1}{2}\)
\(p(B)=p("obtenir les nombres 3")=\frac{1}{6}\)
\(p(A \cup B)=p("obtenir les nombres 2,4,6 ou un nombre 3")=\frac{4}{6}=\frac{2}{3}\)
\(p(A \cap B)=p("obtenir les nombres 2,4,6 et un nombre 3")=p(\varnothing)=0\)
\(P(A)+P(B)=\frac{1}{2}+\frac{1}{6}=\frac{3}{6}+\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)
on a bien \(\color{red}{P(A\cup B)=P(A)+P(B)}\)
Exemple :
\(\color{magenta}{\text{Exemples 12 à 20}}\)
Complément :

Complément :
Complément :