Chapitre VIII Probabilités

• Le tiers des élèves de filière Littéraire sont des garçons :

  \(\frac{1}{3} \times 36=12\)

  Il y a donc 12 garçons en filière Littéraire.

• 60% des élèves de filière Scientifique sont des filles :

  \(60 % \mapsto 36\)

  \(100 % \mapsto N\)

  \(N=\frac{100 \times 36}{60}=60\)

  Il y a donc 60 élèves en filière Scientifique.

• On en déduit le tableau :

  	Economie	Littéraire	Scientifique	STMG	Total
  Fille	25	24	36	12	97
  Garçon	11	12	24	20	67
  Total	36	36	60	32	164

Les élèves de Terminale dans la filière générale sont les élèves de la filière Economie, de la filière Littéraire et de la filière Scientifique :

N=36+36+60=132

La proportion d'élèves de Terminale en filière STMG :

\(\frac{32}{164} =\frac{8}{41}\)

soit en pourcentage

\(\frac{8}{41} \times 100 \simeq 19,5 \%\) arrondi donné au dixième

La proportion de garçons qui sont en filière économique  :

\(\frac{36}{164} =\frac{9}{41}\)

soit en pourcentage

\(\frac{9}{41} \times 100 \simeq 22 \%\) arrondi donné au dixième

La population étudiée est les clients du super marché

Le caractère étudié est le nombre d'articles achetés le jour considéré par chaque client.

• Le nombre moyen d'articles achetés lors de cette journée est :

  \(\overline{M}=\frac{1 \times 4 + 2 \times 6+3 \times 2+5 \times 1+6 \times 8+7 \times 6+8 \times 5+10 \times 2+11 \times 9+15 \times 3+16 \times 1}{47}\)

  \(\iff \overline{M}=\frac{4+12+6+5+48+42+40+20+99+45+16}{47}\)

  \(\iff \overline{M}=\frac{347}{47} \simeq 7,38\) arrondi au centième.

• Le nombre d'articles médian partage la série des nombres d'articles achetés en deux séries de même effectif donc le nombre d'articles médian est la 24ème valeur soit : Médiane=7

  (23 valeurs dans chaque série de nombres d'articles achetés)

• Le premier quartile :

  \(\frac{1}{4} \times 47=11,75 \mapsto 12ème valeur\) donc \(Q_1=3\)

• Le premier quartile :

  \(\frac{3}{4} \times 47=35,25 \mapsto 36ème valeur\) donc \(Q_3=11\)

\(\overline{M}=\frac{10+8+6 \times 3+12 \times 3+16 \times 3}{11}\)

\(\iff \overline{M}=\frac{10+8+18+36+48}{11}\)

\(\iff \overline{M}=\frac{120}{11} \simeq 10,9\)

La moyenne d'Antoine au troisième trimestre est de environ 10,9

Soit \(n\) la ernière note obtenue :

\(\overline{M}=\frac{10+8+6 \times 3+12 \times 3+16 \times 3 + n \times 2}{13} \ge 12\)

\(\iff \overline{M}=\frac{120 + 2n}{13} \ge 12\)

\(\iff 120 + 2n \ge 12 \times 13\)

\(\iff 120 + 2n \ge 156\)

\(\iff 2n \ge 36\)

\(\iff n \ge 18\)

La note minimale d'Antoine pour que sa nouvelle moyenne soit au moins de 12  est 18.

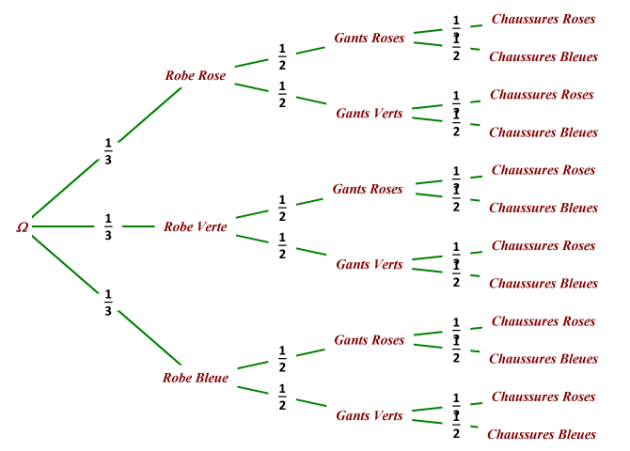
On constate que l'arbre de probabilités comporte 12 feuilles donc Clotilde peut composer 12 tenues différentes

L'événement "Barbante est entièrement habillée en rose." n'est composé que d'une seule issue :

Robe Rose -Gants Roses - Chaussures Roses

\(p(A)= \frac{1}{12}\)

L'événement "Barbante est habillée avec exactement deux articles roses" est composé de 4 issues :

• Robe Rose -Gants Roses - Chaussures Bleues

  Robe Rose -Gants Verts - Chaussures Roses

• Robe Verte -Gants Roses - Chaussures Roses

• Robe Bleue -Gants Roses - Chaussures Roses

\(p(B)= \frac{4}{12}=\frac{1}{3}\)

L'événement "Barbante est habillée avec au moins un article bleu" est l’événement contraire de l'événement "Barbante est habillée avec aucun un article bleu"

Les issues réalisant "Barbante est habillée avec aucun un article bleu" sont :

• Robe Rose - Gants Roses - Chaussures Roses

  Robe Rose - Gants Verts - Chaussures Roses

• Robe Verte - Gants Roses - Chaussures Roses

  Robe Verte - Gants Verts - Chaussures Roses

donc \(p(C)=1-p(\overline{C})= 1-\frac{4}{12}=\frac{8}{12}=\frac{2}{3}\)

L'événement D est l'événement contraire de l'événement A

donc l'événement D est l'événement "Barbante n'est pas habillée entièrement en rose"

donc "Barbante porte au moins un article de couleur bleue ou verte"

\(p(D)=p(\overline{A})=1-p(A)=1- \frac{1}{12}= \frac{12}{12}- \frac{1}{12}\)

\(\iff p(D)= \frac{11}{12}\)

• E=B \(\cap\) C donc l'événement E est l’événement intersection des événements B et C :

"Barbante est habillée avec exactement deux articles roses" et "Barbante est habillée avec au moins un article bleu"

donc "Barbante est habillée avec deux articles roses et un article bleu"

• F=B \(\cup\) C

  donc l'événement F est l'événement union des événements B et C :

  "Barbante est habillée avec exactement deux articles roses ou Barbante est habillée avec au moins un article bleu"

• Les issues réalisant "Barbante est habillée avec deux articles roses et un article bleu" sont :

  • Robe Rose - Gants Roses - Chaussures Bleues

  • Robe bleue - Gants Roses - Chaussures Roses

    donc \(p(E)=\frac{2}{12}=\frac{1}{6}\)

• On a la formule de cours

\(p(A \cup B)=p(A)+p(B)-p( A \cap B)\)

d'où dans notre cas

\(p(F)=p(B \cup C)=p(B)+p(C)-p( B \cap C)\)

\(\iff p(F)=p(B \cup C)=\frac{1}{3}+\frac{2}{3}-\frac{1}{6}\)

\(\iff p(F)=p(B \cup C)=1-\frac{1}{6}\)

\(\iff p(F)=p(B \cup C)=\frac{6}{6}-\frac{1}{6}\)

\(\iff p(F)=p(B \cup C)=\frac{5}{6}\)

Au total on peut réaliser :

\(5 (choix d'une robe) \times 5 (choix d'une veste) \times 5 (choix d'une paire de chaussures ) \times 5 (choix d'une paire de gants) \times 5 (choix d'un bijou)=5^5=3125\)

• T : "La tenue contient au moins deux articles de la même couleur." est l'événement contraire de l'événement \(\overline{T}\)

  "La tenue contient aucun article de la même couleur."

• Nombre de tenues avec aucun article de la même couleur :

\(5 (choix d'une robe parmi 5)\)

\(\times 4 (choix d'une veste avec une couleur déjà utilisée)\)

\(\times 3 (choix d'une paire de chaussures avec deux couleurs déjà utilisées)\)

\(\times 2 (choix d'une paire de gants avec trois couleurs déjà utilisées)\)

\(\times 1 (choix d'un bijou avec quatre couleurs déjà utilisées)=120\)

donc

\(p(\overline{T})=\frac{120}{3125}=\frac{24}{625}\)

\(\iff p(T)=1-p(\overline{T})=1-\frac{24}{625}\)

\(\iff p(T)=1-p(\overline{T})=\frac{625}{625}-\frac{24}{625}\)

\(\iff p(T)=1-p(\overline{T})=\frac{601}{625}\)

La probabilité que la tenue contienne au moins deux articles de la même couleur est \(\frac{601}{625} \simeq 0,96\) arrondi au centième.