I Fonction inverse d'un nombre réel
Exemple :

L'aire du rectangle doit rester égale à 1\(dm^2\).
1.Donner trois possibilités de longueurs différentes (et les largeurs associées) pour les feuilles rectangulaires dont l'aire est égale à 1\(dm^2\)
2. Que vaut la longueur si la largeur vaut 0,5 ?
3. Que vaut \(y\) si \(x=4\) ?
4. Recopier et compléter le tableau de valeurs ci-dessous.
\(x\) | 0,5 | 1 | 1,6 | 2 | 2,5 | 3 | 4 |
|---|---|---|---|---|---|---|---|
\(y\) |
5. Comment semblent évoluer les valeurs de \(y\) lorsque \(x\) augmente ?
6. Quelle formule lie \(x\) et \(y\) ? Donner l'expression de \(y\) en fonction de \(x\)
Complément :
1.Longueur et largeur de trois feuilles rectangulaires dont l'aire est égale à 1\(dm^2\):
\(x=4 \quad et \quad y=0,25\) car \(4 \times 0,25=1\)
\(x=2 \quad et \quad y=0,5\) car \(2 \times 0,5=1\)
\(x=12\quad et \quad y=\frac{1}{12}\) car \(12 \times \frac{1}{12}=1\)
2. La longueur vaut 2 si la largeur vaut 0,5.
car \(0,5 \times 2=1\)
3.Si \(x=4\) alors \(y=0,25\) car \(0,25 \times 4=1\)
4.
\(x\) | 0,5 | 1 | 1,6 | 2 | 2,5 | 3 | 4 |
|---|---|---|---|---|---|---|---|
\(y\) | 2 | 1 | \(\frac{1}{1,6}=0,625\) | 0,5 | \(\frac{1}{2,5}=\frac{1}{\frac{25}{10}}=\frac{10}{25}=0,4\) | \(\frac{1}{3}\) | 0,25 |
5. Les valeurs de \(y\) semblent diminuer lorsque \(x\) augmente.
6. \(x\times y=1\) car les deux dimensions donnent l'aire du rectangle qui est égale à 1\(dm^2\)
\(y=\frac{1}{x}\)
Définition : 1. Fonction inverse d'un nombre réel non nul
\(\color{red}{\textbf{La fonction inverse associe à tout réel } x \textbf{ non nul son unique inverse }}\frac{1}{x}\) .
Définition :
\(\color{red}{\textbf{Complèter le tableau de valeurs ci-dessous :}}\)
\(\color{magenta}{\textbf{Tableau de valeurs}}\)
\(x\) | -2 | -1 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 1 | 2 |
|---|---|---|---|---|---|---|---|---|---|
\(f(x)\) |
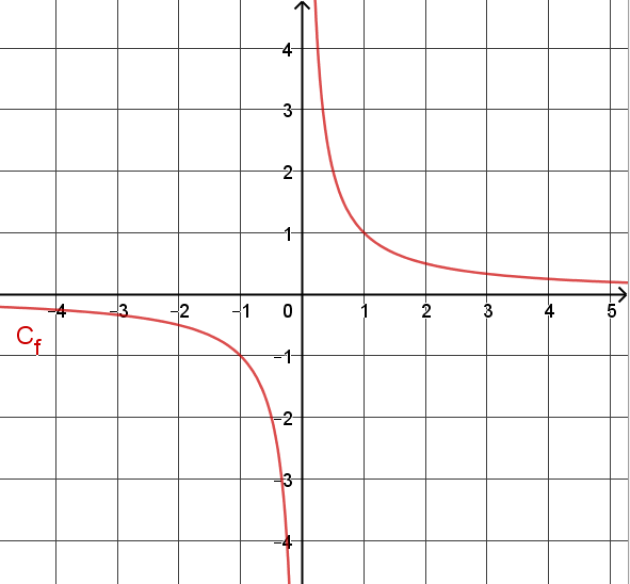
\(\color{red}{\textbf{La fonction inverse est strictement décroissante sur ]-∞;0[ et strictement décroissante sur ]0 ;+∞[.}}\)
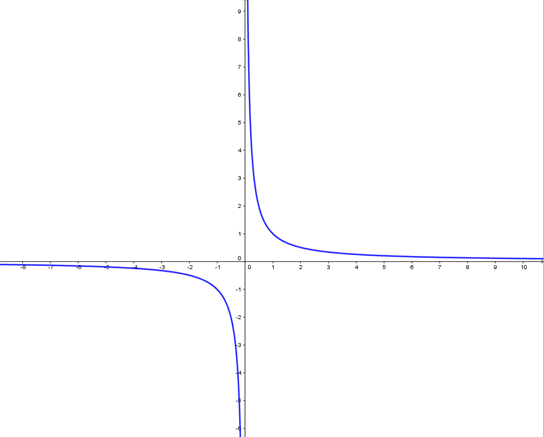
\(\color{red}{\textbf{La courbe représentative de la fonction inverse est une }\underline{hyperbole.}}\)
\(\color{red}{\textbf{La fonction inverse ne s'annule pas sur son ensemble de définition.}}\)
Complément :
\(\color{magenta}{\textbf{Tableau de valeurs}}\)
\(x\) | -2 | -1 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 1 | 2 |
|---|---|---|---|---|---|---|---|---|---|
\(f(x)\) | \(\frac{1}{-2}=-0,5\) | \(\frac{1}{-1}=-1\) | \(\frac{1}{-0,5}=-2\) | \(\frac{1}{-0,25}=-4\) | \(\frac{1}{0}\) impossible | \(\frac{1}{0,25}=4\) | \(\frac{1}{0,5}=2\) | \(\frac{1}{1}=1\) | \(\frac{1}{2}=0,5\) |
Fondamental :
Complément :
\(\color{red}{\textbf{A l'aide de la courbe tracée sous Geogebra complèter le tableau de variations ci-dessous pour la fonction } \frac{1}{x} } :\)
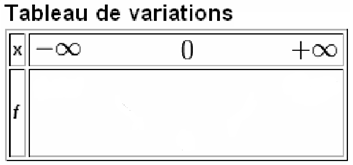
Complément :
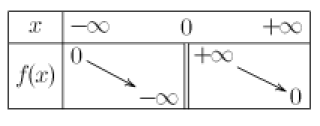
Fondamental :
\(\color{red}{\textbf{La fonction inverse n'est pas définie en }} x=0.\)
\(\color{red}{\textbf{Son ensemble de définition est }} ]-∞ ; 0[∪]0 ; +∞[=R^*\)
Fondamental :
\(\color{red}{\textbf{La fonction inverse est décroissante sur }]-\infty ;0[ \cup ]0 ;+\infty[}\)
Complément : Démonstration :
Soit a et b deux nombres réels \(\color{red}{\textbf{positifs}}\) tels que a < b.
\(f(b)-f(a)=\frac{1}{b}-\frac{1}{a}=\frac{a-b}{ab}\) donc\( f(b)>f(a).\)
Attention :
\(\color{magenta}{\textbf{On ne peut pas dire que la fonction inverse est décroissante globalement sur son ensemble de définition.}}\)
Fondamental : Propriété
\(\color{red}{\textbf{La fonction inverse est } \underline{symétrique } \textbf{par rapport à l'origine du repère.}}\)
\(\color{red}{\textbf{La fonction inverse est } \underline{impaire} f(-x)=-f(x)}\)
Méthode :
Lorsque \(2 < x <5\): \(\frac{1}{5} < \frac{1}{x} < \frac{1}{2} \Leftrightarrow 0,2< \frac{1}{x} < 0,5\)
Lorsque \(-4< x <-2\): \(\frac{1}{-2} < \frac{1}{x} < \frac{1}{-4} \Leftrightarrow -0,5< \frac{1}{x} < -0,25\)
Lorsque \(-3 < x <2\): \(\frac{1}{x} \in ]-\infty ;\frac{1}{-3}[\cup ]\frac{1}{2} ;+\infty[\)
Exemple : Résumé
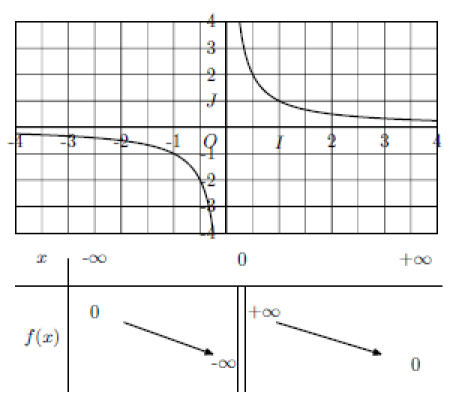
Complément :