II. Fonction inverse d'un nombre réel
Exemple :
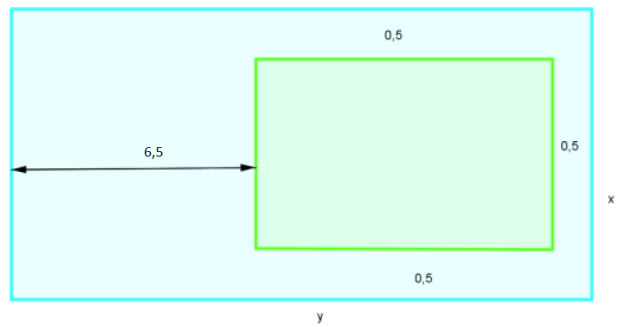
La conception de l'écran d'un nouveau téléphone portable est confiée à un bureau d'études avec les contraintes suivantes :
- L'aire de l'écran doit être 16 \(cm^2\)
- L'écran rectangulaire doit être placé dans le téléphone selon le schéma ci-dessous
1. On cherche les valeurs de et pour lesquelles les dimensions du téléphone répondent aux contraintes du fabricant.
2. On ajoute ensuite une nouvelle contrainte : la somme des dimensions des deux côtés du téléphone doit être 30cm .
Complément :
1. Longueur de l'écran :
\(y-6,5-0,5=y-7\)
Largeur de l'écran :
\(x-0,5-0,5=x-1\)
Aire de l'écran :
\(Longueur \times Largeur=(y-7)\times (x-1)\)
\((y-7)\times (x-1)=16\)
\(y-7=\frac{16}{x-1}\)
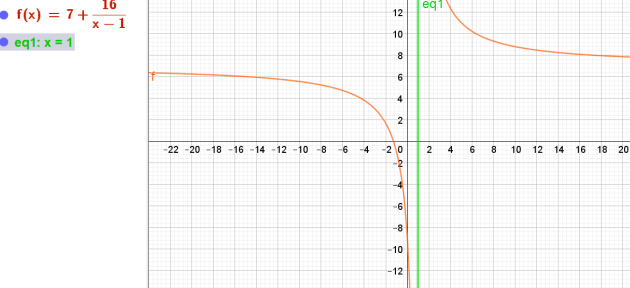
\(y=7+\frac{16}{x-1}\)
\(\frac{16}{x}\) est une courbe obtenue à partir de celle de la fonction \(\frac{1}{x}\) par affinité de rapport 16.
La courbe \(y=7+\frac{16}{x-1}\) est ensuite obtenue à partir de la courbe de la fonction \(\frac{16}{x}\) par translations :
de 7 unités vers le haut selon l'axe vertical (+7).
de 1unité vers la droite selon l'axe horizontal (-1)
Pour qu'on puisse construire le smartphone, il faut que \(x\) soit plus grand que 1 et \(y\) plus grand que 7
donc ce sont les points tels que \(x \in ]1 ;+\infty[\)
Si la somme des dimensions des côtés du téléphone doit être égale à 30,
on doit avoir :
\(x+y=30\)
On doit donc résoudre le système :
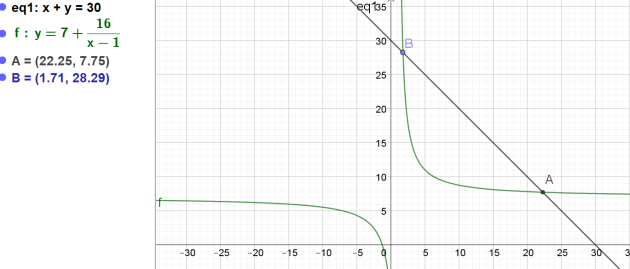
\(\begin{cases}{x+y=30\\y=7+\frac{16}{x-1}}\end{cases}\)
Graphiquement, il semble y avoir deux solutions :
\(\color{magenta}{\textbf{Longueur 22,25 cm et largeur 7,75 cm}}\)
ou
\(\color{magenta}{\textbf{Longueur environ 28,29 cm et largeur environ 1,71 cm}}\)
\(\color{red}{\textbf{Mais la première solution semble plus adaptée à un téléphone car une largeur de 1,71cm est vraiment très fine.}}\)
Méthode : 1) Valeur interdite dans une expression quotient :
\(\color{magenta}{\textbf{Exercice 1}}\)
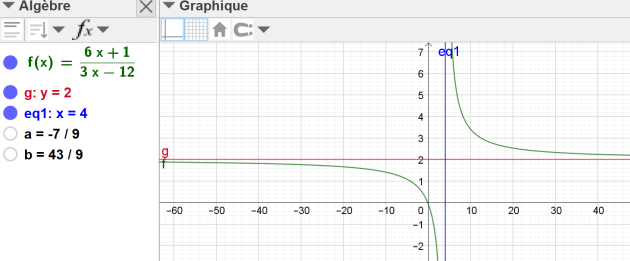
Soit l'expression de la fonction \(f(x)=\frac{6x+1}{3x-12}\)
a) Vérifier que \(f (1)=-\frac{7}{9}\) et que \(f(7)=\frac{43}{9}\).
Complément :
\(f(1)=\frac{6\times 1+1}{3\times 1-12}=\frac{7}{-9}=\frac{-7}{9}\)
\(f(7)=\frac{6\times 7+1}{3\times 7-12}=\frac{43}{9}\)
Exemple :
b) Peut-on calculer \(f(4)\) ?
Complément :
\(f(4)=\frac{6\times 4+1}{3\times 4-12}=\frac{25}{0}\)
\(\color{red}{\textbf{ 4 est DONC une }\underline{valeur \quad interdite} \textbf{ pour ce quotient car on ne peut pas diviser par 0}}\)
Définition :
\(\color{red}{\textbf{Dans une fonction quotient, une valeur de x qui annule le dénominateur est appelée }\underline{\textbf{valeur interdite}} \textbf{ pour le quotient.}}\)
Définition : 2) Représentation graphique de fonctions quotients :
\(\color{red}{\textbf{Une valeur interdite n'a pas d'image, cela se traduit graphiquement par un « trou »}}\)
\(\color{red}{\textbf{dans la courbe au moment du passage par cette valeur interdite.}}\)
Méthode : Tableau de variations de la fonction f du paragraphe 1 (après observation à l'aide
\(\color{magenta}{\textbf{Exercice 2}}\)
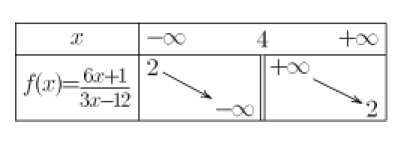
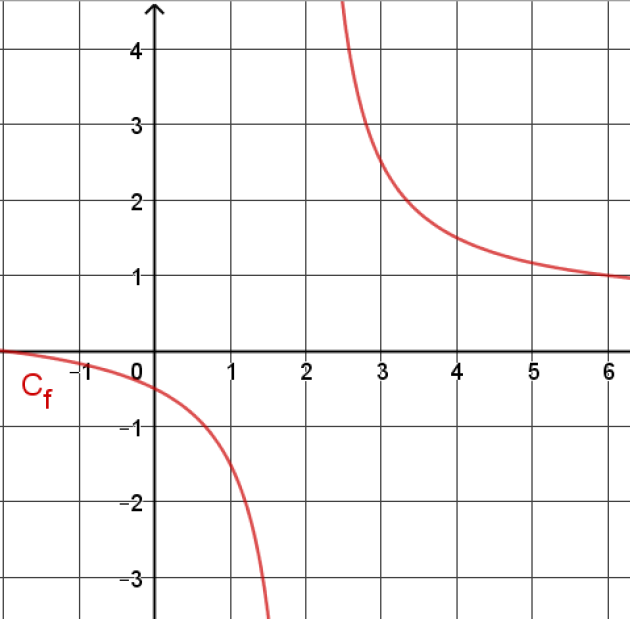
Soit l'expression de la fonction \(f(x)=\frac{6x+1}{3x-12}\)
a. Représenter cette fonction avec Geogebra
b. En déduire le tableau de variation de la fonction \(f\)
Complément :
La valeur interdite est celle qui annule le dénominateur :
\(3x-12=0 \Longleftrightarrow 3x=12 \Longleftrightarrow x=4\)
Méthode : 3) Signe d'un quotient / inéquations quotients :
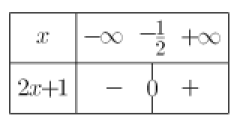
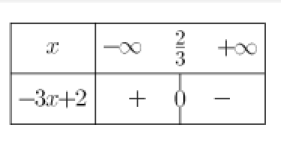
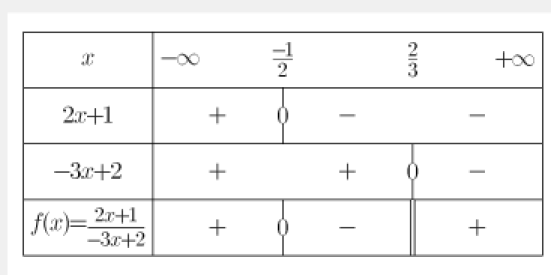
Dresser le tableau de signes de la fonction \(f(x)=\frac{2x+ 1}{-3x+2}\)
Complément :
\(2x+1=0 \Longleftrightarrow 2x=-1 \Longleftrightarrow x=-\frac{1}{2}\)
\(-3x+2=0 \Longleftrightarrow -3x=-2 \Longleftrightarrow x=\frac{-2}{-3}=\frac{2}{3}\)
Fondamental :
\(\color{red}{\textbf{La règle des signes d'un quotient est analogue à la règle des signes d'un produit :}}\)
\(\color{red}{\textbf{un nombre positif divisé par un nombre positif donne un quotient positif.}}\)
\(\color{red}{\textbf{un nombre négatif divisé par un nombre négatif donne un quotient positif.}}\)
\(\color{red}{\textbf{un nombre négatif divisé par un nombre positif donne un nombre négatif.}}\)
\(\color{red}{\textbf{un nombre positif divisé par un nombre négatif donne un nombre négatif.}}\)
Exemple :
\(\color{magenta}{\textbf{Exercice 5}}\)
Résoudre l'inéquation
\(\frac{2x+ 1}{-3x+2}\le 0\)
Complément :
D'après le tableau précédent : \(x \in ]-\infty ;-\frac{1}{2}]\cup]\frac{2}{3} ;+\infty[\)
Exemple :
\(\color{magenta}{\textbf{Exercice 6}}\)
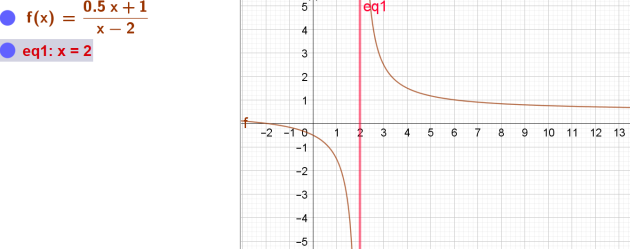
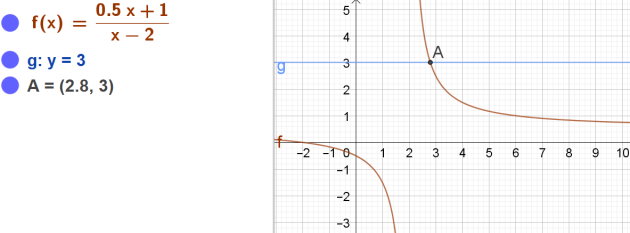
On a représenté ci-contre la courbe représentative de la fonction \(f\) définie par
\(f(x)=\frac{0,5x+1}{x-2}\)
1) Donner la valeur interdite. Faire apparaître cette valeur sur l'axe des abscisses.
2) Résoudre par le calcul l'équation \(f (x)= 3\) puis contrôler graphiquement.
3) Résoudre graphiquement les inéquations
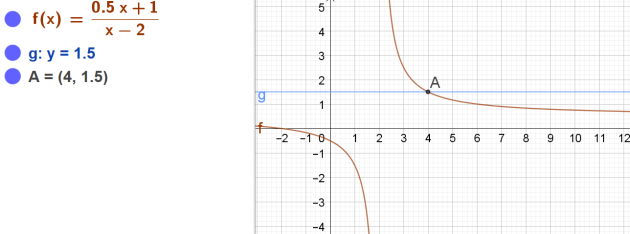
a. \(f (x)\le 3\) b. \(f (x) >1,5\)
Complément :
1.\(x-2=0 \Longleftrightarrow x=2\)
La valeur interdite est donc \(x=2\)
2.\(\frac{0,5x+1}{x-2}\)=3
\(\Longleftrightarrow 0,5x+1=3 \times (x-2)\)
\(\Longleftrightarrow 0,5x+1=3x-6\)
\(\Longleftrightarrow 0,5x=3x-6-1\)
\(\Longleftrightarrow 0,5x-3x=-6-1\)
\(\Longleftrightarrow -2,5x=-7\)
\(\Longleftrightarrow x=\frac{-7}{-2,5}\)
\(\Longleftrightarrow x=\frac{7}{2,5}\)
\(\Longleftrightarrow x=\frac{28}{10}=2,8\)
3) Résoudre graphiquement les inéquations
a. \(f (x)\le 3 \Longleftrightarrow x\in ]-\infty ;2[\cup [ 2,8 ;+\infty[\)
\(b.f (x) >1,5\Longleftrightarrow x \in ]2 ;4[\)
\(\frac{0,5x+1}{x-2}\)>1,5
\(\color{magenta}{Si \quad x-2>0 : \quad (si \quad x>2)}\)
\(\Longleftrightarrow 0,5x+1>1,5 \times (x-2)\)
\(\color{red}{\textbf{On ne change pas le sens d'une inéquation si on multiplie (ou divise)}}\)
\(\color{red}{\textbf{les deux membres de l'inéquation par un même nombre positif}}\)
\(\Longleftrightarrow 0,5x+1>1,5x-3\)
\(\Longleftrightarrow 0,5x>1,5x-3-1\)
\(\Longleftrightarrow 0,5x-1,5x>-4\)
\(\Longleftrightarrow -x>-4\)
\(\Longleftrightarrow x<4\)
donc \(\frac{0,5x+1}{x-2}\)>1,5 si \(x\in ]2;4[\)
\(\color{magenta}{Si \quad x-2<0 : \quad (si \quad x<2)}\)
\(\Longleftrightarrow 0,5x+1<1,5 \times (x-2)\)
\(\color{red}{\textbf{On doit changer le sens d'une inéquation si on multiplie (ou divise) }}\)
\(\color{red}{\textbf{les deux membres de l'inéquation par un même nombre positif}}\)
\(\Longleftrightarrow 0,5x+1<1,5x-3\)
\(\Longleftrightarrow 0,5x<1,5x-3-1\)
\(\Longleftrightarrow 0,5x-1,5x<-4\)
\(\Longleftrightarrow -x<-4\)
\(\Longleftrightarrow x>4\)
donc \(\color{red}{\textbf{Ce cas est impossible car il n'existe pas de valeur de x telle que x<2 et x>4}}\)
\(\color{red}{\textbf{Conclusion : }}\frac{0,5x+1}{x-2}>1,5 \quad si x\in ]2;4[\)
