Exercice : Exercice Rappel : Boule dans Urne
Une urne contient deux boules bleues et une boule rouge, toutes identiques au toucher.
On tire au hasard une boule, puis on la remet dans l'urne avant d'en tirer une seconde.
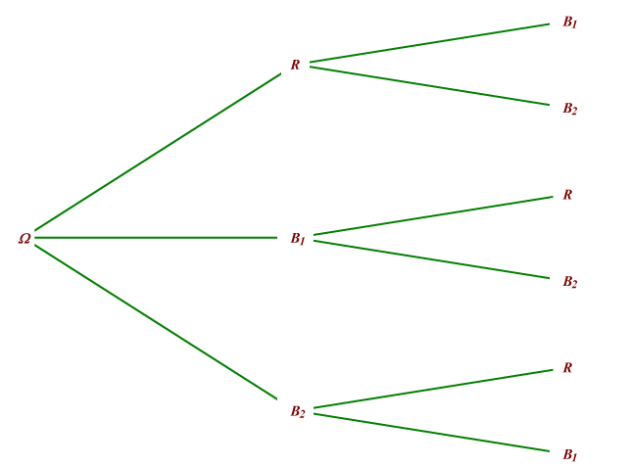
L'arbre des issues de cette expérience aléatoire est représenté ci-dessous.
On admettra qu'on est dans une situation d'équiprobabilité.
a. Déterminer la probabilité des événements suivants :
Question
A : « la première boule tirée est rouge »
Solution
\(p(A)=\frac{3}{9}=\frac{1}{3}\)
Les issues favorables sont :
(\(R-R\) ; \(R-B_1\) ; \(R-B_2\))
Question
B : « les deux boules tirées sont de même couleur »
Solution
\(p(B)=\frac{5}{9}\)
Les issues favorables sont :
(\(R-R\) ; \(B_1-B_1\) ; \(B_1-B_2\) ; \(B_2-B_1\) ; \(B_2-B_2\))
Question
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
Solution
\(p(C)=\frac{7}{9}\)
Les issues favorables sont :
\((R-R ; R-B_1 ;R-B_2 ; B_1-B_1 ; B_1-B_2 ; B_2-B_1 ; B_2-B_2)\)
b. Déterminer la probabilité des événements suivants :
Question
\(\overline{A}\)
Solution
\(\overline{A}\) : « La première boule tirée n'était pas rouge. »
\(p(\overline{A})=1-\frac{1}{3}=\frac{2}{3}\)
Les issues favorables sont :
\((B_1-R ;B_1-B_1 ;B_1-B_2 ; B_2-R ; B_2-B_1 ; B_2-B_2)\)
\(p(\overline{A})=\frac{6}{9}=\frac{2}{3}\)
Question
\(B \cup C\)
Solution
\(p(B \cup C)=p(B)+p(C)-p(B \cap C)\)
\(\iff p(B \cup C)=p(B)+p(C)-p(B \cap C)\)
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
\(\Rightarrow B \cap C\) :
« les deux boules tirées sont de même couleur »
Les issues favorables sont :
\((R-R; B_1-B_1; B_1-B_2 ; B_2-B_1;B_2-B_2)\)
\(P(B \cap C)=p(B)=\frac{5}{9}\)
\(\Rightarrow p(B \cup C)=p(B)+p(C)-p(B)\)
\(\iff p(B \cup C)=p(C)=\frac{7}{9}\)
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
Les issues favorables pour \(B \cup C\) sont :
\((R-R ;B_1-B_1 ;B_1-B_2; B_2-B_1 ; B_2-B_2) \cup (R-B_1 ; R-B_2)\)
donc \(p(B \cup C)=\frac{7}{9}\)
Question
\(A \cap B\)
Solution
A : « la première boule tirée est rouge »
B : « les deux boules tirées sont de même couleur »
L' issue favorable est :
(R-R)
donc \(p(A \cap B)=\frac{1}{9}\)
Question
\(B \cap C\)
Solution
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
\(\Rightarrow B \cap C\) :
« les deux boules tirées sont de même couleur »
Les issues favorables sont :
\((R-R ;B_1-B_1 ;B_1-B_2 ; B_2-B_1 ; B_2-B_2)\)
\(P(B \cap C)=p(B)=\frac{5}{9}\)
2. On change les règles du jeu ainsi :
il n'y a plus de remise ; la première boue tirée est écartée du jeu.
Question
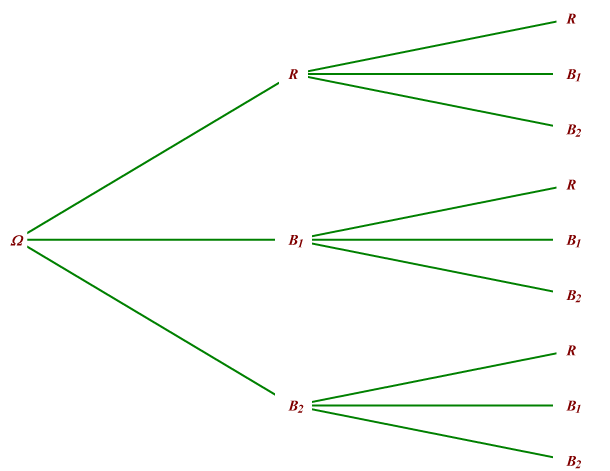
a. Construire l'arbre des issues liées à ce nouveau jeu.
Question
b. Calculer les nouvelles probabilités des événements cités aux questions a. et b. de la question précédente.
Solution
A : « la première boule tirée est rouge »
\(p(A)=\frac{2}{6}=\frac{2}{6}=\frac{1}{3}\)
Les issues favorables sont :
(R-\(B_1\) ; \(R-B_2\))
B : « les deux boules tirées sont de même couleur »
\(p(B)=\frac{2}{6}=\frac{1}{3}\)
Les issues favorables sont :
\(( B_1-B_2 ; B_2-B_1)\)
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
\(p(C)=\frac{4}{6}=\frac{2}{3}\)
Les issues favorables sont :
\((R-B_1 ;R-B_2 ; B_1-B_2 ; B_2-B_1)\)
\(\overline{A}\) : « La première boule tirée n'était pas rouge. »
\(p(\overline{A})=1-\frac{1}{3}=\frac{2}{3}\)
Les issues favorables sont :
\((B_1-R ;B_1-B_2 ;B_2-R ;B_2-B_1)\)
\(p(\overline{A})=\frac{4}{6}=\frac{2}{3}\)
\(p(B \cup C)=p(B)+p(C)-p(B \cap C)\)
\(\iff p(B \cup C)=p(B)+p(C)-p(B \cap C)\)
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
\(\Rightarrow B \cap C\) :
« les deux boules tirées sont de même couleur »
Les issues favorables sont :
(\(B_1-B_2 ;B_2-B_1\))
\(P(B \cap C)=p(B)=\frac{2}{6}=\frac{1}{3}\)
\(\Rightarrow p(B \cup C)=p(B)+p(C)-p(B)\)
\(\iff p(B \cup C)=p(C)=\frac{2}{3}\)
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
Les issues favorables pour \(B \cup C\) sont :
\((B_1-B_2;B_2-B_1) \cup (R-B_1 ; R-B_2)\)
donc \(p(B \cup C)=\frac{4}{6}=\frac{2}{3}\)
A : « la première boule tirée est rouge »
B : « les deux boules tirées sont de même couleur »
Il n'y a pas d' issue favorable à l'événement \(A \cap B\) donc
\(p(A \cap B)=p( \emptyset)=0\)
B : « les deux boules tirées sont de même couleur »
C : « la première boule tirée est rouge ou la seconde boule tirée est bleue. »
\(\Rightarrow B \cap C\) :
« les deux boules tirées sont de même couleur »
Les issues favorables sont :
(\(B_1-B_2 ;B_2-B_1\))
\(P(B \cap C)=p(B)=\frac{2}{6}=\frac{1}{3}\)
Question
c. Quelle est la probabilité de tirer une boule bleue au second tirage alors qu'au premier tirage, on a déjà tirer une boule bleue ?
Solution
\(\color{magenta}{\text{1^{ère} méthode :}}\)
\(b_1\) : « tirer une boule bleue au premier tirage »
\(b_2\) : « tirer une boule bleue au second tirage »
\(p_{b_1}(b_2)\)
Les issues favorables sont :
(\(B_1-B_2 ;B_2-B_1\)) et l'univers des issues possibles est dans ce cas :
(\(B_1-R ;B_1-B_2 ;B_2-R ;B_2-B_1)\)
\(p_{b_1}(b_2)=\frac{2}{4}=\frac{1}{2}\)
\(\color{magenta}{\text{2^{ème} méthode :}}\)
\(b_1\) : « tirer une boule bleue au premier tirage »
\(b_2\) : « tirer une boule bleue au second tirage »
\(p_{b_1}(b_2)=\frac{p(b_1 \cap b_2)}{p(b_1)}\)
\(b_1\cap b_2\) : « tirer une boule bleue au premier et au second tirage »
Les issues favorables sont :
(\(B_1-B_2 ;B_2-B_1\)) donc p(\(b_1\cap b_2\))=\(\frac{2}{6}=\frac{1}{3}\)
\(b_1\): « tirer une boule bleue au premier tirage »
Les issues favorables sont :
(\(B_1-R;B_1-B_2 ;B_2-R;B_2-B_1\))
donc p(\(b_1\))=\(\frac{4}{6}=\frac{2}{3}\)\(\)
\(\iff p_{b_1}(b_2)=\frac{p(b_1\cap b_2)}{p(b_1)}\)\(\)
\(\iff p_{b_1}(b_2)=\frac{\frac{1}{3}}{\frac{2}{3}}\)
\(\iff p_{b_1}(b_2)=\frac{1}{3} \times \frac{3}{2}\)\(\)
\(\iff p_{b_1}(b_2)=\frac{1}{2}\)