Chapitre IX : Probabilités Conditionnelles
Exemple :
\(\color{magenta}{\text{Cours Exemple 1 à 3}}\)
Définition :
\(\color{red}{\textbf{Soit A et B deux évènements d'un univers} \Omega}\)
\(\color{red}{\textbf{ Si p(B)} \ne 0 \textbf{, on appelle probabilité de A sachant B et on note } p_B(A) \textbf{ le nombre}} :\)
\(\color{red}p_B(A) = \frac{p(A \cap B)}{p(B)}\) .
Remarque :
La définition est bien cohérente avec la définition d'une probabilité, c'est à dire :
on a \(0 \le p(A \cap B) \le p(B)\) donc\( p_B(A)\) est bien un réel compris de l'intervalle [0 ; 1] ;
\(p_B(\Omega) = \frac{p(\Omega \cap B)}{p(B)}=\frac{p(B)}{p(B)}=1\) .
Remarque :
Si p(B) et p(A) sont non nuls, on a alors :
\(p(A \cap B) = p_B(A) \times p(B) = p_A(B) \times p(A)\)
Exemple :
\(\color{magenta}{\text{Cours Exemple 4 à 6}}\)
Définition : 2. Arbres pondérés
\(\color{red}{\textbf{Il peut être commode de représenter certaines situations par une arbre pondéré où :}}\)
•\( \color{red}{\textbf{Chaque}}\) \(\color{magenta}{noeud}\) \(\color{red}{\textbf{ de l'arbre correspond à une issue de l'exprérience }}\);
• \(\color{red}{\textbf{Chaque }}\)\(\color{magenta}{"feuille"}\) ,\(\color{red}{\textbf{ ou extrémité de l'arbre représente l'intersection de tous les événements rencontrés}}\)
\(\color{red}{\textbf{sur le chemin menant du départ à cette feuille.}}\)
Fondamental : Règles de l'arbre pondéré (toujours vraies)
\(\color{red}{\textbf{La somme des probabilités des branches issues d'un même noeud vaut 1 :}}\)
\(\color{red}{p_B(A) + p_B(\overline{A}) = 1}\)
\(\color{red}{\textbf{La probabilité d'un chemin est le produit des probabilités des différentes branches qui constituent ce chemin :}}\)
\(\color{red}{p(A \cap B)=p_B(A) \times p(B) }\)
Exemple :
\(\color{magenta}{\text{Cours Exemple 7 à 8}}\)
Définition : 3. Formule des probabilités totales
\(\color{red}{\textbf{Des événements forment une partition de l'univers si les deux conditions suivantes sont réalisées :}}\)
\(\color{red}{\textbf{— ils sont deux à deux disjoints ;}}\)
\(\color{red}{\textbf{— leur réunion forme }\Omega.}\)
\(\color{red}{\textbf{Cela signifie que chaque éventualité de } \Omega \textbf{ appartient à un et un seul de ces évènements.}}\)
Fondamental : Formule des probabilités totales
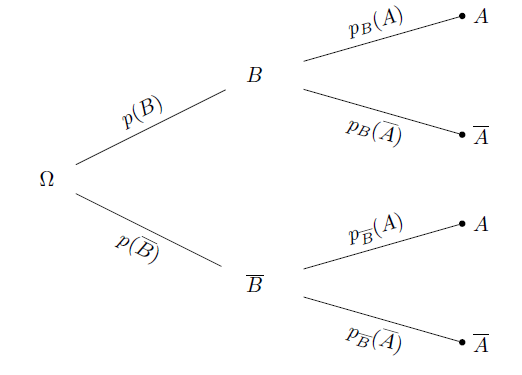
L'évènement A est la réunion de deux chemins : p(A) est la somme des probabilités de ces chemins :
\(p(A) = p(A \cap B) + p(A \cap \overline{B})\)
donc \(\color{\red}{P(A) = P(B) × P_B(A) + P(\overline{B}) × P_{\overline{B}}(A)}\)
Méthode :
\(\color{red}{Generalisation :}\)
\(\color{red}{\textbf{On considère une expérience aléatoire d'univers } \Omega.}\)
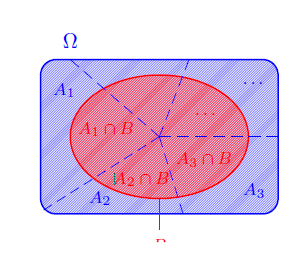
\(\color{red}{\textbf{Si } A_1, A_2, . . .,A_n \textbf{forment une partition de} \Omega , \textbf{alors pour tout évènement B de } \Omega ,\textbf{ on a : }}\)
\(\color{red}{p(B) = p(B \cap A_1) + p(B \cap A_2) + \dots + p(B \cap A_n)}\)
Exemple :
\(\color{magenta}{\text{Cours Exemple 9 à 12}}\)
Définition : II. Événements indépendants
Intuitivement, deux événements sont indépendants si la réalisation de l'un d'entre eux n'influence pas les chances que l'autre se réalise.
Définition :
\(\color{red}{\textbf{On considère A et B deux évènements d'une expérience aléatoire d'univers }} \Omega\)
\(\color{red}{\textbf{tels que A, soient de probabilité non nulle.}}\)
\(\color{red}{\textbf{On a alors :}}\)
\(\color{red}{\textbf{les évènements A et B sont indépendants si et seulement si } p_B(A) = p(A)}\)
\(\color{red}{\textbf{les évènements A et B sont indépendants si et seulement si }p_A(B) = p(B)}\)
\(\color{red}{\textbf{Si A et B deux événements indépendants, alors :}}\)
\(\color{red}{\textbf{• Les événements A et }} \overline{B} \color{red}{\textbf{ sont indépendants ;}}\)
\(\color{red}{\textbf{• Les événements }} \overline{A} \color{red}{\textbf{ et B sont indépendants ;}}\)
\(\color{red}{\textbf{• Les événements }} \overline{A} \color{red}{\textbf{et }} \overline{B} \color{red}{\textbf{ sont indépendants ;}}\)
\(\color{red}{\textbf{• A et B sont indépendants si et seulement si P(A ∩ B) = P(A) × P(B)}}\)
Complément : Démonstration (facultatif)
\(p_B(A) = \frac{p(A \cap B)}{p(B)}\) , donc \(p_B(A) = p(A)\) si et seulement si \(\frac{p(A \cap B)}{p(B)} = p(A)\),
c'est-à-dire \(p(A \cap B) = p(A) \times p(B)\), c'est- à-dire A et B indépendants.
— on a \(B \cap \overline{A} = B \ (B \cap A)\) (faire un diagramme), donc :
\(p(B \cap \overline{A}) = p(B)- p(B \cap A) ;\)
on obtient donc :
\(p_{\overline{A}}(B)\)
\(=\frac{p(B \cap \overline{A}}{p(\overline{A})}\)
\(=\frac{p(B) - p(B \cap A)}{1 - p(A)}\)
\(=\frac{p(B) - p(B) \times p(A)}{1 - p(A)}\)
\(= \frac{p(B)(1 - p(A))}{ 1 - p(A)}\)
\(= p(B)\)
Exemple :
\(\color{magenta}{\text{Cours Exemple 13 à 18}}\)