Rappel
En 1654, Blaise Pascal (1623 ; 1662) entretient avec Pierre de Fermat (1601 ; 1665) des correspondances sur le thème des jeux de hasard et d'espérance de gain qui les mènent à exposer une théorie nouvelle :
les calculs de probabilités.
Ils s'intéressent à la résolution de problèmes de dénombrement comme par exemple celui du Chevalier de Méré :
« Comment distribuer équitablement la mise à un jeu de hasard interrompu avant la fin de la partie ? »

Complément :
On attribue l'origine du mot hasard à l'arabe « al-zahr » signifiant à l'origine « dés » et ayant pris la signification de « chance »,
car il désigna jusqu'au XII e siècle un jeu de dés, mais aussi tous les domaines relevant de la « science de la Chance ».
Définition : Expérience aléatoire
\(\color{red}{\textbf{Lorsque le résultat d'une expérience dépend du hasard, on parle d'expérience aléatoire.}}\)
Exemple :
\(\color{magenta}{L'expérience aléatoire 1:}\)
"On lance un dé non pipé à six faces et on note le résultat de la face supérieure."
\(\color{magenta}{L'expérience aléatoire 2:}\)
"On tire au hasard une carte dans un jeu de 32 cartes."
\(\color{magenta}{L'expérience aléatoire 3:}\)
"On tire au hasard une boule dans une urne contenant 2 boules vertes, 2 boules rouges et 1 boule noire."
Définition : Univers
\(\color{red}{\textbf{On appelle univers (noté U ou} \Omega\textbf{ ) l'ensemble de tous les résultats possibles..}}\)
Exemple : Exemples :
\(Ω_1={1;2;3;4;5;6}\)
\(Ω_2={7;8;9;10;V;D;R;As}\)
\(Ω_3={\textbf{2 boule V;2 boule R;1 boule N}}\)
Remarque :
Nous ne traiterons que le cas où l'univers a un nombre fini d'éléments.
Définition : Evènement
\(\color{red}{\textbf{On appelle événement (noté A, B, C, · · · ) toute partie de l'univers.}}\)
On note A ⊂ \(\Omega\) et on lit "A est inclus dans \(\Omega\)"
Exemple : Exemples :
\(\color{magenta}{Pour l'expérience 1 :}\)
L'événement A : "On obtient un résultat pair." On a donc : A = {2 ; 4 ; 6}. \(p(A)=\frac{3}{6}=\frac{1}{2}\)
L'événement B : "On obtient le chiffre 3". On a donc : B = {3}. \(p(B)=\frac{1}{6}\)
Définition :
L'événement B : "On obtient le chiffre 3" est un événement élémentaire.
On appelle \(\color{magenta}{\textbf{événement élémentaire}}\), ou éventualité, tout événement qui ne contient qu'un seul élément
Exemple :
\(\color{magenta}{Pour l'expérience 2:}\)
L'événement A : "Tirer un roi" On a donc :\( A = {R_{Coeur} ;R_{Carreau} ; R_{Trèfle} ; R_{Pique}}.\) \(p(A)=\frac{4}{32}\)
L'événement B : "Tirer le roi de coeur" On a donc : \(B = {R_{Coeur}}\). \(p(B)=\frac{1}{32}\)
L'événement B est un évènement élémentaire.
Exemple :
\(\color{magenta}{Pour l'expérience 3:}\)
L'événement A : "On ne tire pas la boule noire" On a donc : A = {2V ;2R}. \(p(A)=\frac{4}{5}\)
Exemple : Exemple 1:
Soit l'expérience aléatoire (dont les issues dépendent du hasard) :
"On lance un dé à six faces et on regarde le résultat."
L'ensemble de toutes les issues possibles est Ω = {1 ; 2 ; 3 ; 4 ; 5 ; 6}. (univers des issues possibles)
(univers des possibles)
Chaque issue a pour probabilité \(\frac{1}{6}\)
Quelle est la probabilité des événements suivants :
A : « Obtenir un nombre pair » \(p(A)=\frac{3}{6}=\frac{1}{2}\)
B : « Obtenir un 3 » \(p(B)=\frac{1}{6}\)
C : « Obtenir un nombre inférieur ou égal à 2 » \(p(C)=\frac{2}{6}=\frac{1}{3}\)
D : « Obtenir un nombre strictement supérieur à 4 » \(p(D)=\frac{2}{6}=\frac{1}{3}\)
L'événement "non A" est noté \(\overline{A}\) . Il est constitué des éléments de \(\Omega\) n'appartenant pas à A.
\(\overline{A}\): « Obtenir un nombre impair » constitué des issues {1 ;3 ;5} \(p(\overline{A})=\frac{3}{6}=\frac{1}{2}\)
\(\overline{A}\) est aussi appelé \(\color{magenta}{\textbf{événement contraire}}\) de A.
\(p(\overline{A})=1-p(A)\)
Définition : E : « Obtenir 7 » p(E)=0
E est un \(\color{magenta}{\textbf{événement impossible}}\) un l'événement qui ne contient aucun élément.
On le note ⊘ : P(⊘) = 0
Définition : F : « Obtenir un nombre inférieur ou égal à 6 » p(F)=1
F est un \(\color{magenta}{\textbf{événement certain}}\) , l'événement qui contient tous les éléments.
On le note \(\Omega\): \(P(\Omega) = 1\)
Complément :
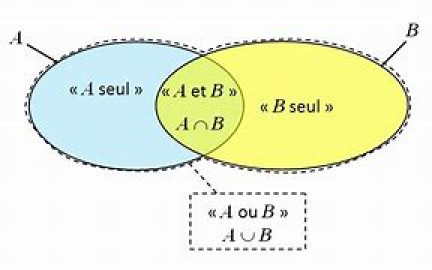
Exemple : A ∩ B :
L'événement "A et B" est noté A ∩ B . Il est constitué des éléments appartenant à la fois à A et à B.
Obtenir un nombre pair (A) et obtenir un 3 (B) donc A ∩ B=⊘ et p(A ∩ B )=0
car cet événement est également un événement impossible (il ne contient aucun événement)
Définition :
Si A ∩ B = ⊘ , on dit que les événements A et B sont \(\color{magenta}{incompatibles}\) ou \(\color{magenta}{disjoints}\)
Exemple : A ∪B :
L'événement "A ou B" est noté A ∪ B . Il est constitué des éléments appartenant soit à A, soit à B, soit aux deux.
Donc A ∪B={2 ;3 ;4 ;6} ("Obtenir un nombre pair" ou "Obtenir un 3") pour notre exemple
\(p(A ∪ B )= \frac{4}{6}=\frac{2}{3}\)
Fondamental :
Pour tous les événements A et B de \(\Omega\)
\(P(A ∪ B) = P(A) + P(B) − P(A ∩ B)\).
Dans notre exemple :
\(P(A ∪ B) = \frac{2}{3}\)
\(P(A)=\frac{1}{2}\)
\(P(B)=\frac{1}{6}\)
\(P(A ∩ B)=0\).
\(P(A) + P(B) − P(A ∩ B)=\frac{1}{2}+\frac{1}{6}=\frac{3}{6}+\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)
Fondamental :
Cas particulier : Si A et B sont deux événements disjoints de \(\Omega\)
\(P(A ∩ B) = P(⊘) = 0\) donc \(P(A ∪ B) = P(A) + P(B) − P(A ∩ B)\) se simplifie en :
\(P(A ∪ B) = P(A) + P(B)\) (comme dans le cas de notre exemple )