Exercice : Boules dans urnes
Une urne contient deux boules bleues et une boule rouge, toutes identiques au toucher.
Question
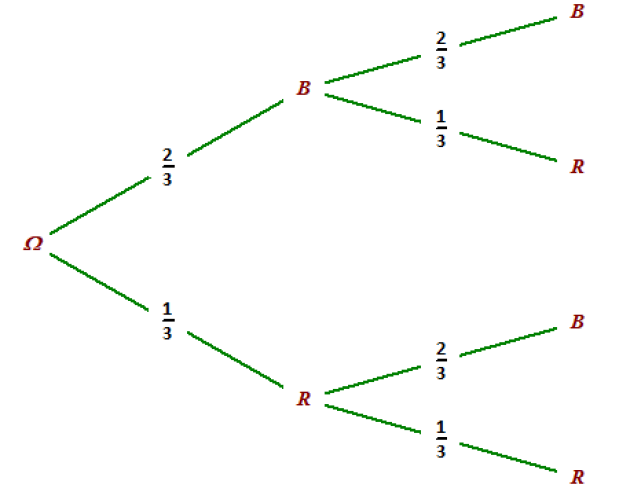
1. On tire une boule puis on la remet dans l'urne avant d'en tirer une seconde.
Représenter cette situation par un arbre de probabilité.
Question
2.On admettra qu'on est dans une situation d'équiprobabilité.
a. Déterminer la probabilité des événements suivants :
A : “La premiere boule tirée est rouge”.
Solution
\(p(A)=p(“La premiere boule tirée est rouge”)=\frac{1}{3}\)
Question
B : “Les deux boules tirées sont de même couleur”
Solution
\(p(B)=p(\textbf{“Les deux boules tirées sont de même couleur”})=\frac{1}{3}\times \frac{1}{3} + \frac{2}{3} \times \frac{2}{3}=\frac{1}{9} + \frac{4}{9} = \frac{5}{9}\)
Question
C : “La première boule tirée est rouge ou la seconde boule tirée est bleu”.
Solution
\(p(C)=p( \textbf{“La première boule tirée est rouge ou la seconde boule tirée est bleue”})=\frac{1}{3} + \frac{2}{3} \times \frac{2}{3}=\frac{1}{3} + \frac{4}{9}=\frac{3}{9} + \frac{4}{9}=\frac{7}{9}\)
ou
\(p(C)=p(\overline{\textbf{"La première boule tirée est bleue et la seconde boule tirée est rouge"}})=1-\frac{2}{3}\times\frac{1}{3}=1-\frac{2}{9}=\frac{7}{9}\)
Question
b. Déterminer la probabilité des événements suivants :
\(\overline{A}\) ;\(\)
Solution
\(p(\overline{A})=1-p(A)=1-\frac{1}{3}=p(“La premier boule tirée est bleue”)=\frac{2}{3}\)
Question
\(B \cup C\) ;\(\)
Solution
p(\(B \cup C\))=p(“Les deux boules tirées sont de même couleur" ou "La première boule tirée est rouge ou la seconde boule tirée est bleu”)=p("La première boule tirée est rouge ou la seconde boule tirée est bleu”))=p(C)=\(\frac{7}{9}\)
ou p(\(B \cup C\))\(=p(B)+p(C)-p(B \cap C)\)
p(\(B \cup C\))=p("Les deux boules tirées sont de même couleur")+p("La première boule tirée est rouge ou la seconde boule tirée est bleue”)-p("Les deux boules tirées sont de même couleur" et "La première boule tirée est rouge ou la seconde boule tirée est bleue”)
p(\(B \cup C\))=p("Les deux boules tirées sont de même couleur")+p("La première boule tirée est rouge ou la seconde boule tirée est bleue”)-p("Les deux boules tirées sont de même couleur")
p(\(B \cup C\))\(=p(B)+p(C)-p(B)\)
p(\(B \cup C\))=p(C)=\(\frac{7}{9}\)
Question
\(A\cap B\) ;\(\)
Solution
\(p(A\cap B)=p(“\textbf{La premier boule tirée est rouge” et "Les deux boules tirées sont de même couleur”)=p("Les deux boules tirées ont rouges"})=\frac{1}{3}\times \frac{1}{3} =\frac{1}{9}\)
Question
\(B \cap C\)
Solution
\(p( B \cap C)=p(B)=\frac{5}{9}\)
Question
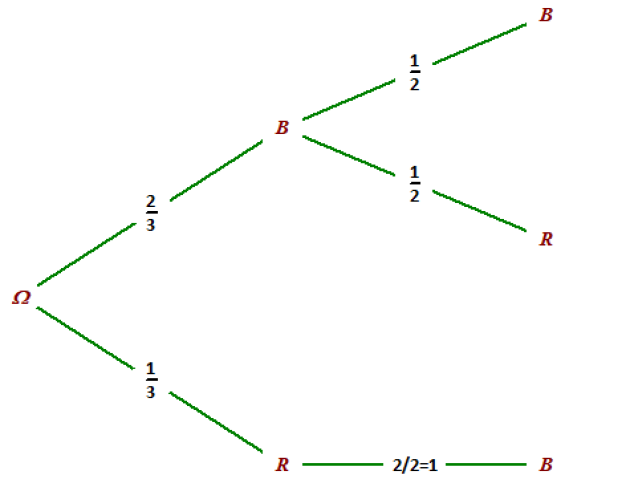
3. On change les règles de ce jeu ainsi : il n'y a plus de remise ; la première boule tirée est écartée du jeu.
a. Construire l'arbre des issues lié à ce nouveau jeu.
Question
b. Calculer les nouvelles probabilités des événements cités aux question a. et b. de la question précédente.
Solution
\(p(A)=p(“La premiere boule tirée est rouge”)=\frac{1}{3}\)
\(p(B)=p(\textbf{“Les deux boules tirées sont de même couleur”})=\frac{2}{3}\times \frac{1}{2} =\frac{1}{3}\)
\(p(C)=p( \textbf{“La première boule tirée est rouge ou la seconde boule tirée est bleue”})=\frac{1}{3} + \frac{2}{3} \times \frac{1}{2}=\frac{1}{3} + \frac{1}{3}=\frac{2}{3}\)
ou
\(p(C)=p(\overline{\textbf{"La première boule tirée est bleue et la seconde boule tirée est rouge"}})=1-\frac{2}{3}\times\frac{1}{2}=1-\frac{1}{3}=\frac{2}{3}\)
\(p(\overline{A})=1-p(A)=1-\frac{1}{3}=p(“La premier boule tirée est bleue”)=\frac{2}{3}\)
p(\(B \cup C\))=p(“Les deux boules tirées sont de même couleur" ou "La première boule tirée est rouge ou la seconde boule tirée est bleu”)=p("La première boule tirée est rouge ou la seconde boule tirée est bleu”))=p(C)=\(\frac{2}{3}\)
ou p(\(B \cup C\))\(=p(B)+p(C)-p(B \cap C)\)
p(\(B \cup C\))=p("Les deux boules tirées sont de même couleur")+p("La première boule tirée est rouge ou la seconde boule tirée est bleue”)-p("Les deux boules tirées sont de même couleur" et "La première boule tirée est rouge ou la seconde boule tirée est bleue”)
p(\(B \cup C\))=p("Les deux boules tirées sont de même couleur")+p("La première boule tirée est rouge ou la seconde boule tirée est bleue”)-p("Les deux boules tirées sont de même couleur")
p(\(B \cup C\))\(=p(B)+p(C)-p(B)\)
p(\(B \cup C\))=p(C)=\(\frac{2}{3}\)
\(p(A\cap B)=p(\textbf{“La premier boule tirée est rouge” et "Les deux boules tirées sont de même couleur”})=p(\varnothing)=0\)
\(p( B \cap C)=p(B)=\frac{1}{3}\)
Question
c. Quel est la probabilité de tirée une boule bleu au second tirage alors que lors du premier tirage, on a déjà tiré une boule bleu ?
Solution
\(1^{er} cas : p_B(B)=\frac{2}{3}\)
\(2^{ème} cas :\)\(p_B(B)=\frac{1}{2}\)