Exercice : Produit Scalaire - Fonction Dérivée 1
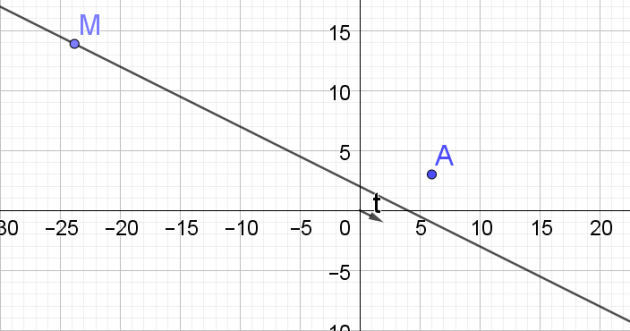
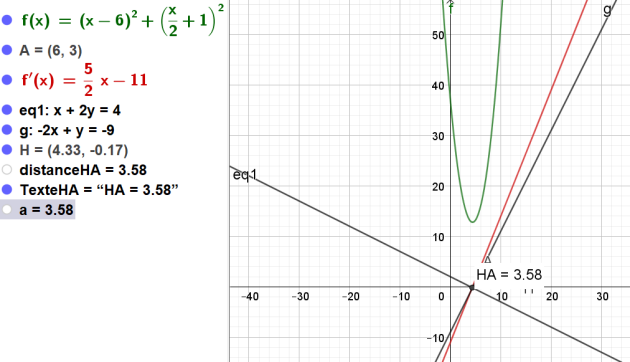
Dans un repère orthonormal du plan, on considère d'une part le point \(A\left(6;3\right)\) et, d'autre part, la droite (d) dont une équation cartésienne est \(x+2y=4.\)
Question
Faire une figure
Question
1. Montrer que le vecteur \({\displaystyle \overrightarrow{t}:\left[\begin{array}{c}2\\-1\end{array}\right]}\) est un vecteur directeur de la droite (d).
Solution
L'équation de la droite \(x+2y=4\) s'écrit aussi \(2y=-x+4\)
son équation réduite est donc \(y=-\frac{1}{2}x+2\)
Un vecteur directeur de la droite est donc \((1 ;-\frac{1}{2})\)
En multipliant ce vecteur par 2 on obtient le vecteur \(\vec{t}\)
qui est donc également un vecteur directeur de la droite (d)
Question
2. On considère un point M de coordonnées \(\left(x;y\right)\) appartenant à la droite (d).
a. Montrer que la longueur AM est telle que:
\(AM^{2}=\left(x-6\right)^{2}+\left(y-3\right)^{2}\).
Solution
\(AM=\sqrt{(x_M-x_A)^2+(y_M-y_A)^2}\)
\(\iff AM=\sqrt{(x-6)^2+(y-3)^2}\)
\(\iff AM^2=\left(x-6\right)^{2}+\left(y-3\right)^{2}.\)
Question
b. En déduire que l'on a \(AM^{2}=\left(x-6\right)^{2}+\left(\frac{x}{2}+1\right)^{2}\).
Solution
\(M \in(d)\) donc les coordonnées du point M vérifient :
\(y=-\frac{1}{2}x-2\)
On remplace alors par cette relation dans le calcul de la longueur \(AM^2\) :
\(AM^2=\left(x-6\right)^{2}+\left(y-3\right)^{2}.\)
\(\iff AM^2=\left(x-6\right)^{2}+\left(-\frac{1}{2}x+2-3\right)^{2}.\)
\(\iff AM^2=\left(x-6\right)^{2}+\left(-\frac{1}{2}x+2-3\right)^{2}\)
\(\iff AM^2=\left(x-6\right)^{2}+\left(-\frac{1}{2}x-1\right)^{2}\)
\(\iff AM^2=\left(x-6\right)^{2}+\left(\frac{1}{2}x+1\right)^{2}\)
Question
3. Montrer que le produit scalaire \(\overrightarrow{t}\cdot\overrightarrow{AM}\)
est le nombre réel \(\frac{5x}{2}-11\).
Solution
\(\overrightarrow{t}\cdot\overrightarrow{AM}\)
\(=\left (\begin{array}{c}2\\-1\end{array}\right) .\left (\begin{array}{c}x-6\\-\frac{1}{2}x- 1\end{array}\right)\)
\(=2(x-6)-1\times(-\frac{1}{2}x-1)\)
\(=2x-12+\frac{1}{2}x+1\)
\(=\frac{4}{2}x-\frac{1}{2}x-11\)
\(=\frac{5}{2}x-11\)
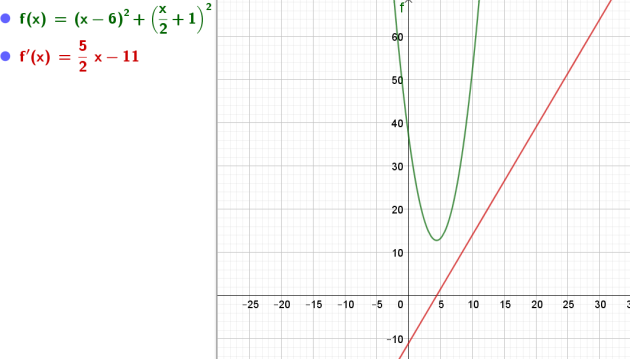
4. On considère la fonction h qui associe à un nombre réel quelconque \(x\) le nombre réel \(h\left(x\right)=\left(x-6\right)^{2}+\left(\frac{x}{2}+1\right)^{2}\).
Question
a. Calculer la dérivée de la fonction \(h\).
Indice
\(u^2\mapsto 2u \times u'\)
Solution
\(h'\left(x\right)=2\left(x-6\right) \times 1+2 \left(\frac{x}{2}+1\right) \times \frac{1}{2}\)
\(\iff h'\left(x\right)=2\left(x-6\right) + \left(\frac{x}{2}+1\right)\)
\(\iff h'\left(x\right)=2x-12+\frac{x}{2}+1\)
\(\iff h'\left(x\right)=\frac{5x}{2}-11\)
Question
b. Pour quelle valeur de l'abscisse \(x\) du point M la fonction \(h\) atteint-elle son minimum?
Solution
\(h'\left(x\right)=\frac{5x}{2}-11\)
\(h'\left(x\right)=0\)
\(\iff \frac{5x}{2}-11=0\)
\(\iff \frac{5x}{2}=11\)
\(\iff 5x=22\)
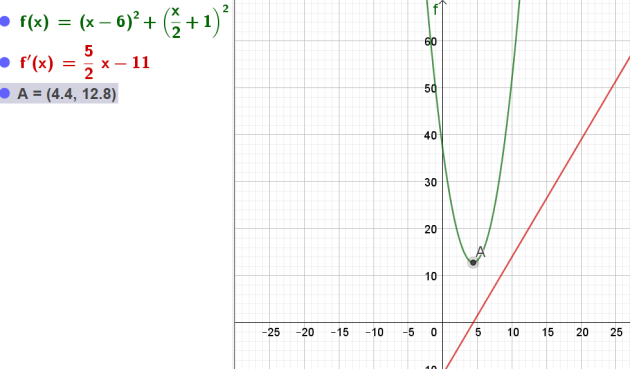
\(\iff x=\frac{22}{5}=4,4\)
\(h\left(4,4\right)=\left(4,4-6\right)^{2}+\left(\frac{4,4}{2}+1\right)^{2}\)
\(\iff h\left(4,4\right)=\left(-1,6\right)^{2}+\left(3,2\right)^{2}\)
\(\iff h\left(4,4\right)=2,56+10,24=12,8\)
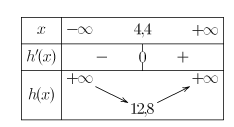
La valeur de l'abscisse \(x\) du point M où la fonction \(h\) atteint son minimum est 4,4.
La valeur de \(h\) est alors de 12,8.
Question
c. Quel est le lien entre ce résultat et la question précédente ?
Solution
La valeur \(AM^2\) est donc minimum pour une abscisse du point M de 4,4.
Cette valeur est alors de 12,8.
La distance \(AM\) est donc minimum pour une abscisse du point M de 4,4.
Cette distance est alors de \(\sqrt{12,8}\)
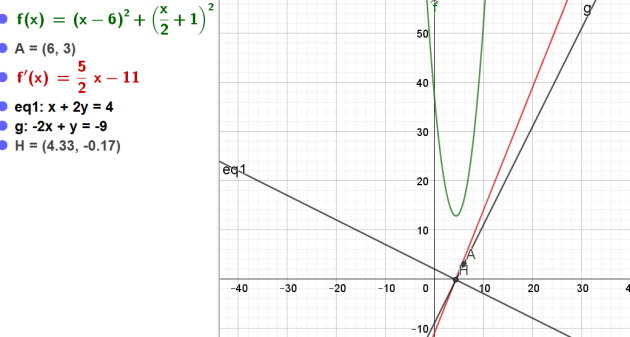
La valeur 4,4 correspond donc à l'abscisse du projeté orthogonal du point A
sur la droite (d).
