Exercice : Droites 2
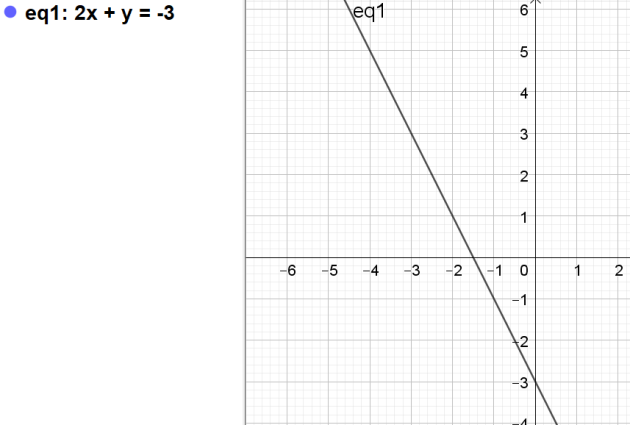
(D) est la droite d'équation \(2x+y+3=0\) dans un repère orthonormé.
Question
1.a. Tracer cette droite.
Question
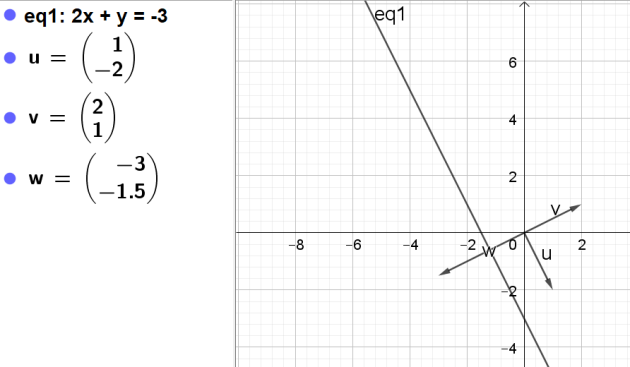
b. Prouver que le vecteur
\(\vec{u}=\left(\begin{array}{c}2\\1\end{array}\right)\) est normal à (D).
Solution
Un vecteur directeur de la droite (D) est le vecteur
\(\left( \begin{array}{c}1\\-2\end{array} \right)\)
\(\left( \begin{array}{c}2\\1\end{array}\right).\left( \begin{array}{c}1\\-2\end{array} \right)=1\times 2+(-2)\times 1\)
\(\iff \left( \begin{array}{c}2\\1\end{array} \right).\left( \begin{array}{c}1\\-2\end{array} \right)=2-2=0\)
donc le vecteur
\(\vec{u}=\left(\begin{array}{c}2\\1\end{array}\right)\)
est normal à (D).
Question
c. Déterminer les coordonnées d'un vecteur \(\vec{u'}\) normal à D (différent de \(\vec{u}\)).
Que peut-on dire des vecteurs \(\vec{u}\) et \vec{u'} ?
Solution
Tout vecteur colinéaire au vecteur \(\vec{u}\) convient.
Exemple : \(\vec{w}\)
Question
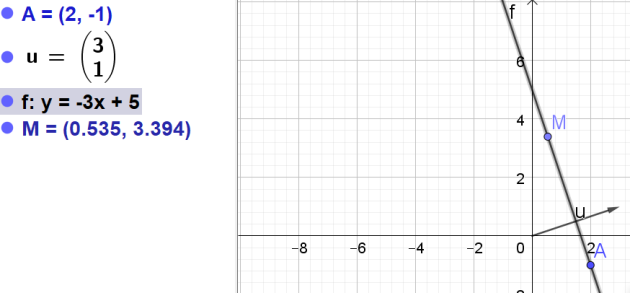
2. Réciproque : on considère la droite \(\Delta\) passant par A(2;-1) et de vecteur normal \(\vec{u}\)\(\begin{pmatrix}3\\1\end{pmatrix}.\)
Déterminer une équation cartésienne de la droite \(\Delta\) dans un repère orthonormé.
Solution
\(\vec{AM}\) et \(\vec{u}\) sont orthogonaux
donc \(\vec{AM}.\vec{u}=0\)
\(\left(\begin{array}{c}x_M-x_A\\y_M-y_A\end{array} \right).\left( \begin{array}{c}3\\1\end{array} \right)\)
=\(\left( \begin{array}{c}x-2\\y-(-1)\end{array} \right).\left( \begin{array}{c}3\\1\end{array}\right)\)
=\(\left(\begin{array}{c}x-2\\y+1\end{array}\right)\)
=\(3(x-2)+1(y+1)=0\)
\(\iff 3x-6+y+1=0\)
\(\iff 3x-5+y=0\)
\(\iff y=-3x+5\)
Question
3. Plus généralement, montrer que dans un repère orthonormé (O,\(\vec{i}\),\(\vec{j}\)),une droite \(\Delta\) de vecteur \(\vec{u}\begin{pmatrix}a\\b\end{pmatrix}\)
admet une équation cartésienne du type \(ax+by+c=0\).
Solution
\(\vec{AM}\) et \(\vec{u}\) sont orthogonaux
donc \(\vec{AM}.\vec{u}=0\)
\(\left( \begin{array}{c}x_M-x_A\\y_M-y_A\end{array} \right).\left(\begin{array}{c}a\\b\end{array} \right)=0\)
\(\left( \begin{array}{c}x-x_A\\y-y_A\end{array} \right).\left(\begin{array}{c}a\\b\end{array}\right)=0\)
\(\iff a(x-x_A)+b(y-y_A)=0\)
\(\iff ax-ax_A+by-by_A=0\)
\(\iff ax+by-ax_A-by_A=0\)
En posant \(c=-ax_A-by_A\)
On trouve l'équation de la droite (D) sous la forme
\(ax+by+c=0\)