Exercice : Droites 1
On se place dans un plan muni d'un repère orthonormal.
Répondre de manière argumentée au questions ci-dessous.
Question
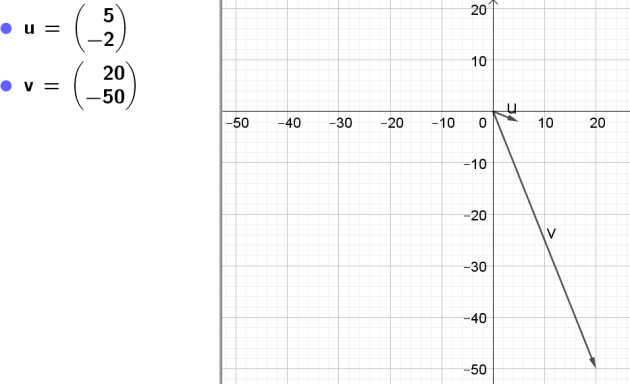
1. Les vecteurs de coordonnées respectives \(\left(\begin{array}{c}5\\-2\end{array}\right)\)
et \(\left(\begin{array}{c}20\\-50\end{array}\right)\) sont-ils orthogonaux?
Solution
\(\left( \begin{array}{c}5\\-2\end{array}\right ) .\left( \begin{array}{c}20\\-50\end{array} \right )\)
\(=5 \times 20 + (-2) \times (-50)\)
\(=200\)
Les deux vecteurs ne sont donc pas orthogonaux.
Question
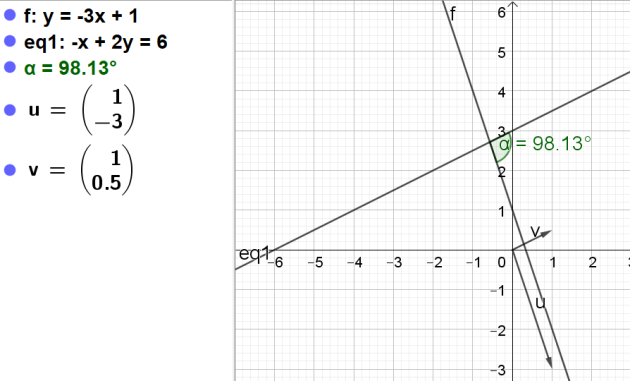
2. Les droites d'équations respectives \(y=-3x+1\) et \(-x+2y=6\) sont-elles perpendiculaires?
Solution
Un vecteur directeur de la droite d'équation \(y=-3x+1\) est \(\vec{u}=\left( \begin{array}{c}1\\-3\end{array} \right)\)
\(||\vec{u}||=\sqrt{1^2+(-3)^2}=\sqrt{1+9}=\sqrt{10}\)
un vecteur directeur de la droite d'équation \(-x+2y=6\) est \(\vec{v}=\left( \begin{array}{c}1\\\frac{1}{2}\end{array} \right)\)
\(2y=x+6\)
\(\iff y=\frac{x}{2}+3\)
\(||\vec{v}||=\sqrt{1^2+(\frac{1}{2})^2}=\sqrt{1+\frac{1}{4}}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}\)
Calcul du produit scalaire des deux vecteurs directeurs choisis :
\(\vec{u}.\vec{v}=\left( \begin{array}{c}1\\-3\end{array} \right) .\left( \begin{array}{c}1\\\frac{1}{2}\end{array} \right)=1-3\frac{1}{2}=-\frac{1}{2}\)
donc les deux vecteurs ne sont pas orthogonaux, les deux droites ne sont donc pas perpendiculaires.
\(\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}|| \times cos(\vec{u} ;\vec{v})\)
\(\iff -\frac{1}{2}=\sqrt{10} \times \frac{\sqrt{5}}{2} \times cos(\vec{u} ;\vec{v})\)
\(\iff -\frac{1}{2}=\frac{\sqrt{50}}{2} \times cos(\vec{u} ;\vec{v})\)
\(\iff -\frac{1}{2}=\frac{\sqrt{25\times 2}}{2} \times cos(\vec{u} ;\vec{v})\)
\(\iff -\frac{1}{2}=\frac{5\sqrt{2}}{2} \times cos(\vec{u} ;\vec{v})\)
\(\iff \frac{-\frac{1}{2}}{\frac{5\sqrt{2}}{2}} =cos(\vec{u} ;\vec{v})\)
\(\iff cos(\vec{u} ;\vec{v})=\frac{-\frac{1}{2}}{\frac{5\sqrt{2}}{2}}\)
\(\iff cos(\vec{u} ;\vec{v})=-\frac{1}{2} \times \frac{2}{5\sqrt{2}}\)
\(\iff cos(\vec{u} ;\vec{v})=-\frac{1}{5\sqrt{2}}\)
\(\iff cos(\vec{u} ;\vec{v})=-\frac{\sqrt{2}}{10}\)
\(\iff (\vec{u} ;\vec{v})=Arccos(-\frac{\sqrt{2}}{10})\)
\(\iff (\vec{u} ;\vec{v})=Arccos(-\frac{\sqrt{2}}{10})\simeq98,13°\)
Question
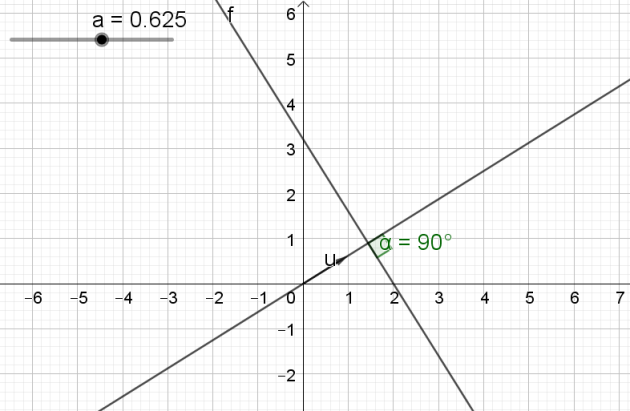
3. Pour quelle valeur du nombre réel \(a\) le vecteur de coordonnées \(\left(\begin{array}{c}1\\a\end{array}\right)\)
est-il normal à la droite d'équation \(y=-1,6\left(x-2\right)\)?
Solution
Un vecteur directeur de la droite d'équation \(y=-1,6\left(x-2\right)\) est
\(\left(\begin{array}{c}1\\-1,6\end{array}\right)\)
\(\left(\begin{array}{c}1\\a\end{array}\right).\left(\begin{array}{c}1\\-1,6\end{array}\right)=1-1,6a\)
Donc le vecteur de coordonnées \(\left(\begin{array}{c}1\\a\end{array}\right)\)
est normal à la droite d'équation \(y=-1,6\left(x-2\right)\) si et seulement si
\(1-1,6a=0\) c'est à dire si 1,6a=1 ou encore \(\color{red}{a=\frac{1}{1,6}=0,625}\)
