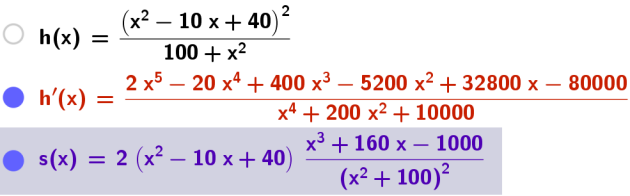Exercice : Produit Scalaire - Fonction Dérivée 2
\(\color{magenta}{Problème :}\)
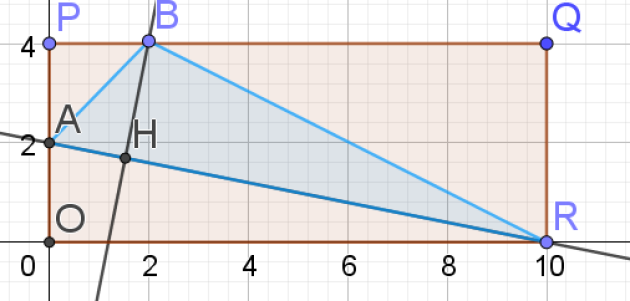
Sur la figure ci-dessus OPQR est un rectangle de longueur 10 et de largeur 4.
On considère un nombre réel a appartenant à l'intervalle \(\left[0;4\right]\) et les deux points A et B tels que:
• A est le point du segment \(\left[OP\right]\) tel que la longueur OA est égale à a;
• B est le point du segment \(\left[PQ\right]\) tel que la longueur PB est égale à a.
Le point H est le point d'intersection de la droite \left(AR\right) et de la perpendiculaire à \(\left(AR\right)\) issue de B.
Le principal objectif du problème est l'étude de la hauteur BH du triangle ABR.
\(\color{magenta}{Partie A : }\)
Dans cette partie, on se limite à l'étude du cas particulier où a=2.
Question
1. Calculer l'aire de chacun des triangles AOR, BRQ et APB.
Solution
\(Aire_{AOR}=\frac{OR\times OA}{2}=\frac{10\times2}{2}=10\)
\(Aire_{BRQ}=\frac{BQ\times QR}{2}=\frac{8\times4}{2}=16\)
\(Aire_{APB}=\frac{PA\times PB}{2}=\frac{2\times2}{2}=2\)
Question
2. En déduire que l'aire du triangle ABR est 12.
Solution
\(Aire_{ABR}=Aire_{OPQR}-Aire_{AOR}-Aire_{BRQ}-Aire_{APB}=4\times10-10-16-2=12\)
Question
3. Calculer la longueur AR.
Solution
En utilisant le théorème de Pythagore dans le triangle AOR rectangle en O
\(AR^2=AO^2+OR^2=2^2+10^2=4+100=104\)
\(AR=\sqrt{104}\)
Question
4. En déduire BH.
Solution
\(Aire_{ABR}=\frac{AR\times BH}{2}=\frac{\sqrt{104}\times BH}{2}=12\)
\(BH=\frac{12 \times 2}{\sqrt{104}}=\frac{24}{\sqrt{104}}\simeq2,35\)
Question
\(\color{magenta}{Partie B}\)
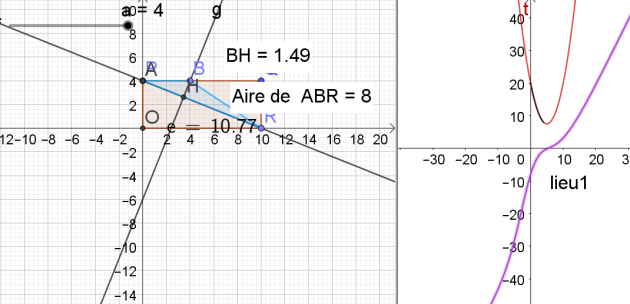
Réaliser une figure dynamique avec GeoGebra permettant d'observer la hauteur BH (et sa longueur) lorsque le paramètre a varie dans l'intervalle \(\left[0;4\right]\).
\(\color{magenta}{Partie C}\)
On revient au cas général où le nombre réel a est un élément quelconque de l'intervalle \(\left[0;4\right]\).
Question
1. Démontrer que l'aire du triangle ABR est:
\(\frac{a^{2}}{2}-5a+20\).
Solution
\(Aire_{AOR}=\frac{OR\times OA}{2}=\frac{10\times a}{2}=5a\)
\(Aire_{BRQ}=\frac{BQ\times QR}{2}=\frac{(10-a)\times4}{2}=-2a+20\)
\(Aire_{APB}=\frac{PA\times PB}{2}=\frac{(4-a)\times a}{2}=\frac{-a^2+4a}{2}\)
2.\(Aire_{ABR}=Aire_{OPQR}-Aire_{AOR}-Aire_{BRQ}-Aire_{APB}\)
\(=4\times10-5a-(-2a+20)-(\frac{-a^2+4a}{2})\)
\(=40-5a+2a-20+\frac{a^2-4a}{2}\)
\(=40-5a+2a-20+\frac{a^2}{2}-2a\)
\(Aire_{ABR}=\frac{a^2}{2}-5a+20\)
Question
2. En déduire l'expression de la hauteur BH en fonction du nombre réel a.
Solution
En utilisant le théorème de Pythagore dans le triangle AOR rectangle en O
\(AR^2=AO^2+OR^2=a^2+10^2\)
\(Aire_{ABR}=\frac{AR\times BH}{2}\)
\(=\frac{\sqrt{a^2+10^2}\times BH}{2}\)
\(=\frac{a^2}{2}-5a+20\)
\(BH=\frac{(\frac{a^2}{2}-5a+20)\times 2}{\sqrt{a^2+10^2}}\)
\(\iff BH=\frac{a^2-10a+40}{\sqrt{a^2+100}}\)
\(\color{magenta}{Partie D}\)
À la suite des résultats précédents, on définit la fonction \(h\),
sur l'intervalle \(\left[0;4\right], \)par :
\(h\left(x\right)=\frac{\left(x^{2}-10x+40\right)^{2}}{100+x^{2}}\).
À l'aide d'un logiciel de calcul formel (Geogebra), on a obtenu
l'expression suivante de la dérivée de la fonction \(h\):
\(h'\left(x\right)=\frac{2(x^{2}-10x+40)\left(x^{3}+160x-1000\right)}{\left(x^{2}+100\right)^{2}}\)
Question
1.a.Vérifier la formule donnée pour la dérivée \(h'\)
Indice
\(u^2\mapsto2u \times u'\)
\(\frac{u}{v}\mapsto \frac{u'v-uv'}{v^2}\)
Solution
\(\begin{cases}u=\left(x^{2}-10x+40\right)^{2}\\v=100+x^{2}\end{cases}\)
\(\begin{cases}u'=2\left(x^{2}-10x+40\right) \times (2x-10)\\v'=2x\end{cases}\)
\(\begin{cases}u'=(4x-20)\left(x^{2}-10x+40\right)\\v'=2x\end{cases}\)
\(h'\left(x\right)=\frac{(4x-20)\left(x^{2}-10x+40\right)(100+x^{2})-\left(x^{2}-10x+40\right)^{2}\times 2x}{(100+x^{2})^2}\).
\(\iff h'\left(x\right)=\frac{\left(x^{2}-10x+40\right)((4x-20)(100+x^{2})-2x\left(x^{2}-10x+40\right))}{(100+x^{2})^2}\).
\(\iff h'\left(x\right)=\frac{\left(x^{2}-10x+40\right)(400x+4x^3-2000-20x^2-(2x^3-20x+80x))}{(100+x^{2})^2}\)
\(\iff h'\left(x\right)=\frac{\left(x^{2}-10x+40\right)(400x+4x^3-2000-20x^2-2x^3+20x^2-80x))}{(100+x^{2})^2}\)
\(\iff h'\left(x\right)=\frac{\left(x^{2}-10x+40\right)(2x^3+320x-2000)}{(100+x^{2})^2}\)
\(\iff h'\left(x\right)=2\frac{\left(x^{2}-10x+40\right)(x^3+160x-1000)}{(100+x^{2})^2}\)
Question
b. Démontrer que, pour tout nombre réel \(x\) appartenant à l'intervalle \(\left[0;4\right]\), on a: \(x^{2}-10x+40>0\).
Solution
\(x^{2}-10x+40=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-10)^2-4 \times 1 \times 40\)
\(\iff \Delta=100-160=-60<0\)
donc l'équation \(x^{2}-10x+40=0\) n'a pas de solution
et le trinôme \(x^{2}-10x+40\) est toujours du signe de \(a\)
Or ici \(a=1\) (1\(x^2\)) donc \(x^{2}-10x+40>0\)
Question
c. On considère la fonction \(f\) définie sur l'intervalle \(\left[0;4\right]\) par \(f(x)=x^{3}+160x-1000\)
Étudier le signe de la fonction \(f\) sur son intervalle de définition.
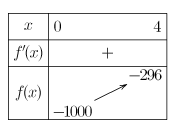
On tracera le tableau de signes de la fonction \(f\) sur \(\left[0;4\right]\)
Solution
\(f'(x)=3x^{2}+160\)
\(x^2\ge 0\) pour \(x\in \mathbb{R}\)
\(\iff 3x^{2} \ge 0\) pour \(x\in \mathbb{R}\)
\(\iff 3x^{2}+160 \ge 160>0\) pour \(x\in \mathbb{R}\)
donc la fonction \(f\) est strictement croissante sur \(\mathbb{R}\)
\(f(0)=0^{3}+160 \times 0-1000=-1000\)
\(f(4)=4^{3}+160 \times 4-1000=64+640-1000=-296\)
donc la fonction \(f\) est négative sur [0 ;4]
Question
c. Déduire de ce qui précède que la fonction h est strictement décroissante sur l'intervalle \(\left[0;4\right]\).
Solution
\(h\left(0\right)=\frac{\left(0^{2}-10\times 0+40\right)^{2}}{100+0^{2}}\)
\(h\left(0\right)=\frac{40^{2}}{100}\)
\(h\left(0\right)=\frac{16000}{100}=16\)
\(h\left(4\right)=\frac{\left(4^{2}-10\times 4+40\right)^{2}}{100+4^{2}}\)
\(h\left(4\right)=\frac{(16-40+40)^{2}}{116}\)
\(h\left(4\right)=\frac{16^2}{116}=\frac{256}{116}\)
\(h\left(4\right)=\frac{64}{29}\)
Question
2. Que peut-on en déduire pour la hauteur BH en fonction de la valeur du paramètre \(a\)
Solution
\(h(a)=BH^2(a)\)
donc lorsque \(h\) est minimum, \(BH^2\) est minimum
et donc \(BH\) est minimum.
Finalement BH est minimum lorsque \(a=4\)
et la valeur minimum de BH
est \(\sqrt{\frac{64}{29}}=\frac{8}{\sqrt{29}}=\frac{8\sqrt{29}}{29}\)
