Exercice : Exercice 3

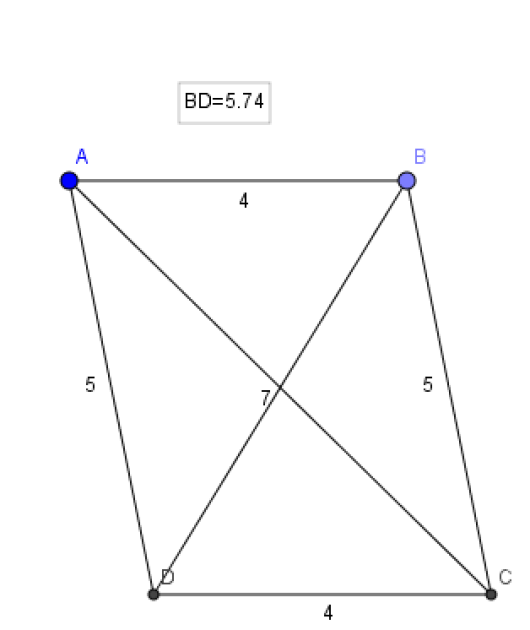
ABCD est un parallélogramme avec AB = 4, AD = 5 et AC = 7.

Question

1.Faire une figure.

Solution

Question

2. Calculer \(\vec{AB} . \vec{AD}\)

Indice

\(\vec{u}.\vec{v}=\frac{1}{2} ( ||\vec{u} +\vec{v}||^2- ||\vec{u}||^2- ||\vec{v}||^2 )\)

Solution

\(\vec{AB}.\vec{AD}\)=\(\vec{AB}.\vec{BC}\)

\(\iff \vec{AB}.\vec{AD}=\frac{1}{2} (||\vec{AB}+\vec{BC}||^2- ||\vec{AB}||^2- ||\vec{BC}||^2\)

\(\iff \vec{AB}.\vec{AD}=\frac{1}{2} (||\vec{AC}||^2- ||\vec{AB}||^2- ||\vec{BC}||^2 )\)

\(\iff \vec{AB}.\vec{AD}=\frac{1}{2}(7^2-4^2-5^2 )=\frac{1}{2}( 49-16-25)=\frac{1}{2} \times 8=4\)

Question

3. Calculer en développant : \(( \vec{AD}- \vec{AB} )^2\).

Solution

\(( \vec{AD}-\vec{AB})^2=AD^2-2\vec{AD}.\vec{AB}+AB^2=5^2-2*4+4^2=25-8+16=33\)

Question

4. En déduire la longueur BD.

Indice

A quel vecteur est égal \(\vec{AD}- \vec{AB}\)

Solution

\(\vec{AD}- \vec{AB}=\vec{AD}+ \vec{BA}= \vec{BA}+ \vec{AD}\)

Donc \(BD^2\)=33 et \(BD=\sqrt{33}\)