Exercice : Jeu télévisé
À un jeu télévisé, un candidat doit tirer successivement et avec remise deux boules d'une urne qui en contient dix :
une marquée 500 €, trois marquées 100 € et les autres marquées 0 €.
Question
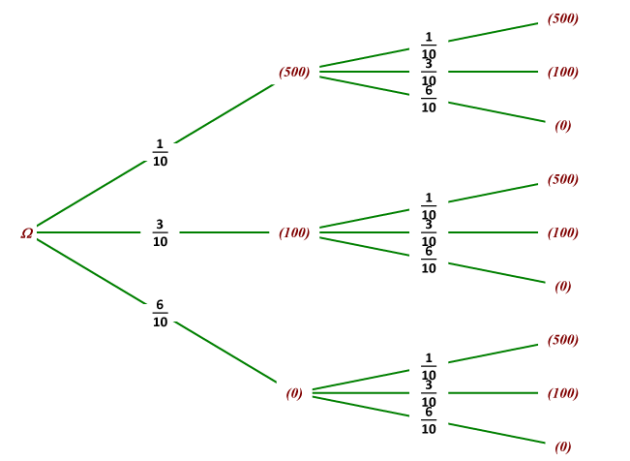
1. Représenter la situation par une arbre pondéré.
Le candidat gagne le total des montants figurant sur les deux boules tirées.
On note \(S\) la variable aléatoire qui associe, à chaque partie, la somme d'argent gagnée par le candidat.
Question
2. Déterminer la loi de probabilité de la variable aléatoire \(S\).
Solution
Les tirages sont indépendants (avec remise).
On calcule les probabilités pour chaque Somme.
S | Combinaison possibles | Calcul de la probabilité | Résultat p(S) |
|---|---|---|---|
0 | 0 €+0 € | \(\frac{6}{10}×\frac{6}{10}\) | 0,36 |
100 | 100 €+0 € ou 0 €+100 € | \(2×(\frac{3}{10}×\frac{6}{10})\) | 0,36 |
200 | 100 €+100 € | \(\frac{3}{10}×\frac{3}{10}\) | 0,09 |
500 | 500 €+0 €ou 0 €+500 € | \(2×(\frac{1}{10}×\frac{6}{10})\) | 0,12 |
600 | 500 €+100 € ou 100 €+500 € | \(2×(\frac{1}{10}×\frac{3}{10})\) | 0,06 |
1000 | 500 €+500 € | \(\frac{1}{10}×\frac{1}{10}\) | 0,01 |
Vérification
La somme des probabilités est :
0,36+0,36+0,09+0,12+0,06+0,01=1.0,36+0,36+0,09+0,12+0,06+0,01=1.
S(€) | 0 | 100 | 200 | 500 | 600 | 1000 |
|---|---|---|---|---|---|---|
p(S) | 0,36 | 0,36 | 0,09 | 0,12 | 0,06 | 0,01 |
Question
3. Déterminer l'espérance de la variable aléatoire \(S\).
Solution
\(E(S)=0×0,36+100×0,36+200×0,09+500×0,12+600×0,06+(1000×0,01)\)
\(\iff E(S)=36+18+60+36+10\)
\(\iff E(S)=160€.\)
Le candidat peut espérer gagner 160 € en moyenne par partie.
Ce résultat est cohérent avec la composition de l’urne :
La probabilité de tirer une boule à 500 € est faible (\(\frac{1}{10}\)), mais son impact sur l’espérance est significatif grâce à son montant élevé.
Pour valider, on peut aussi calculer l’espérance par tirage, puis multiplier par 2 (car deux tirages indépendants) :
Espérance par tirage :
\(\frac{1}{10}×500+\frac{3}{10}×100+\frac{6}{10}×0=50+30+0=80 €.101×500+103×100+106×0=50+30+0=80€\)
Espérance totale pour 2 tirages : \(2×80=160 €\)
Question
4. Déterminer la variance et l'écart-type de la variable aléatoire \(S\).
Solution
\(V(S)=(0-160)^2×0,36+(100-160)^2×0,36+(200-160)^2×0,09+(500-160)^2×0,12+(600-160)^2×0,06+(1000-160)^2×0,01\)
Calcul de\( E(S^2)\) :
On calcule la moyenne des carrés des gains :
\(E(S^2)=0^2×0,36+100^2×0,36+200^2×0,09+500^2×0,12+600^2×0,06+1000^2×0,01\)
\(\iff E(S^2)=0+3 600+3 600+30 000+21 600+10 000=68 800\)
La variance est définie par :
\(V(S)=E(S^2)−(E(S))^2=68 800−(160)^2=68 800−25 600=43 200\)
L’écart-type est la racine carrée de la variance :
\(σ(S)=\sqrt{43 200}≈207,85 €\)
Interprétation
La variance 43 200 € mesure la dispersion des gains autour de l’espérance.
L’écart-type (≈207,85 €) indique que les gains s’écartent en moyenne environ de 208 € de la valeur espérée de \(160 €\) ce qui traduit un risque élevé (dû aux boules à 500 € et 1000 €).