Exercice : DM 2022
Exercice 1
Un responsable de magasin achète des composants électroniques auprès de deux fournisseurs (et seulement deux fournisseurs) dont 25% au premier fournisseur
La proportion de composants défectueux est de 3% chez le premier fournisseur et de 2% chez le second.
On note :
D : l’événement “le composant est défectueux” ;
\(F_1\): l’événement “le composant provient du premier fournisseur”;
\(F_2\) : l’événement “le composant provient du second fournisseur”.
Question
1.Justifier soigneusement que \(p(F_2)=0,75\)
Indice
On justifiera que les événements \(F_1\) et \(F_2\) forment une partition de l'univers.
Question
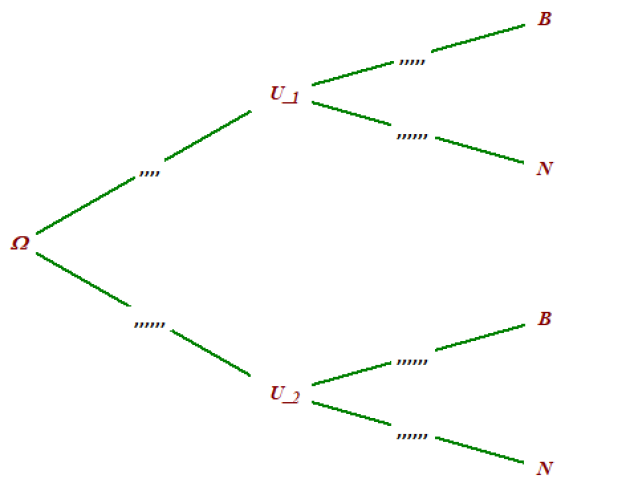
2. Dresser un arbre de probabilité correspondant à cette situation.
Indice
Les valeurs à indiquer sur les branches sont à écrire en valeurs décimales.
Justifier les valeurs des probabilités non données par l'énoncé.
Question
3. Calculer \(p(D \cap F1)\)
Question
4.Démontrer que p(D)=0,0225
Question
3. Sachant qu'un composant est défectueux, quelle est la probabilité qu'il provienne du premier fournisseurnotée \(p_D(F_1)\)?
On arrondira sa valeur au millième près.
Indice
On utilisera la formule des probabilités conditionnelles.
Exercice 2
On dispose de deux urnes \(U_1\) et \(U_2\) .
L'urne \(U_1\) contient trois boules blanches et une boule noire .
L'urne \(U_2\) contient une boule blanche et deux boules noires.
On lance un dé non truqué.
Si le dé donne un numéro inférieur ou égal à 2, on tire une boule dans l'urne \(U_1\) .
Sinon on tire une boule dans l'urne \(U_2\) .
(On suppose que les boules sont indiscernables au toucher)
Question
2. Calculer la probabilité de tirer une boule blanche.
Question
3. On a tiré une boule blanche. Calculer le probabilité qu'elle provienne de l'urne \(U_1\).Cette probabilité est \(p_B(U_1)\)
Exercice 3
Le tableau suivant donne la répartition de 150 stagiaires en fonction de la langue choisie et de l'activité sportive choisie.
Tennis | Equitation | Voile | |
|---|---|---|---|
Anglais | 45 | 18 | 27 |
Allemand | 33 | 9 | 18 |
On choisit un élève au hasard.
Question
1. Les événements « étudier l'allemand » et « pratiquer le tennis » sont-ils indépendants ?
Question
2. Les événements « étudier l'anglais » et « pratiquer la voile » sont-ils indépendants ?
Exercice 4
On dispose d'un dé cubique pipé dont les faces sont numérotées de 1 à 6.
On désigne par \(p_k\) la probabilité d'obtenir, lors d'un lancer la face numérotée \(k\) (\(k\) est un entier et 1⩽\(k\)⩽6).
Les nombres \(p_1, p_2, p_3, p_4, p_5, p_6\), dans cet ordre, sont six
termes consécutifs d'une suite arithmétique de raison r ;
Question
1. Montrer que la condition précédente est équivalente à l'équation:
\(6p_1+15r=1\)
Indice
La somme des probabilités des 6 faces est égale à 1.
Les nombres \(p_1, p_2, p_4\) dans cet ordre, sont trois termes
consécutifs d'une suite géométrique de raison q.
Question
2. Montrer que cette deuxième condition est équivalente au système :
\(\begin{cases}p_2=qp_1=p_1+r\\p_4=q^2\times p_1=p_1+3r\end{cases}\)
\(\iff \begin{cases}3p_2=3qp_1=3p_1+3r\\p_4=q^2\times p_1=p_1+3r\end{cases}\)
Question
3. En soustrayant les deux lignes du deuxième système de la question 2,
montrer que \(3qp_1-q^2 \times p_1=2p_1\)
Question
4. En déduire que la raison \(q\) de la suite géométrique vérifie :
\(3q-q^2=2 \iff q^2-3q+2=0\)
Question
5. En déduire, en résolvant l'équation de la question 4, que les valeurs possibles de la raison de la suite géométrique sont soit \(q=1\) , soit \(q=2\)
Question
6. Si \(q=1\), montrer que la raison \(r\) de la suite arithmétique est 0
et que \(p_1=p_2=\cdots=p_6\).
\(\color{red}{\text{Ce cas est donc à exclure car le dé est pipé.}}\)
Indice
On remplacera en particulier la raison \(q\) par la valeur 1 dans l'équation
\(p_2=qp_1=p_1+r\) obtenue à la question 2.
Question
7. Si \(q=2\), montrer que la raison \(r\) de la suite arithmétique est \(p_1\)
et que \(p_1=\frac{1}{21}\)
Solution
On remplacera en particulier la raison \(q\) par la valeur 2 dans l'équation
\(p_2=qp_1=p_1+r\) obtenue à la question 2.
On remplacera en particulier la raison \(r\) par la valeur \(p_1\) dans l'équation
\(6p_1+15r=1\) obtenue à la question 1.
Question
8.En déduire que :
\(\begin{cases}p_1=\frac{1}{21}\\p_2=\frac{2}{21}\\p_3=\frac{3}{21}\\p_4=\frac{4}{21}\\p_5=\frac{5}{21}\\p_6=\frac{6}{21}\end{cases}\)
On lance ce dé une fois et on considère les événements suivants :
A : “le nombre obtenu est pair” ;
B : “le nombre obtenu est supérieur ou égal à 3” ;
C : “le nombre obtenu est 3 ou 4”.
Question
9.a. Calculer la probabilité de chacun de ces événements.
Question
b. Calculer la probabilité que le nombre obtenu soit supérieur
ou égal à 3 sachant qu'il est pair.
Question
c. Les événements A et B sont-ils indépendants ?
Question
d.Les événements A et C sont-ils indépendants ?