Exercice : Devoir Classe A : Probabilités Conditionnelles et Exponentielles
Exercice 1
Louis et Carla mangent chacun une part (pas forcément de même taille) de galette des rois dans laquelle leur père à caché deux fèves.
Ils décident que celui ou celle qui trouve au moins une fève dans sa part sera roi ou reine et portera donc une couronne.
Sans fève dans sa part, pas de trône ni de couronne.
Le père, au vu de la taille de leur part, fait les calculs suivants :
la probabilité pour que son fils soit roi est de \(\frac{7}{16}\)
et, si Louis n'est pas roi, alors sa fille a 8 chances sur 9 d'être reine.
On note
L : l'événement "Louis est roi"
et
C : l'événement "Carla est reine".
Question
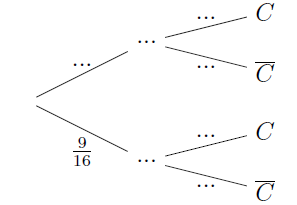
1. Reporter sur votre copie et compléter avec les données de l'énoncé, l'arbre de probabilités suivant :
Il faudra attendre la question 3 pour terminer de compléter l'arbre de probabilités.
Solution
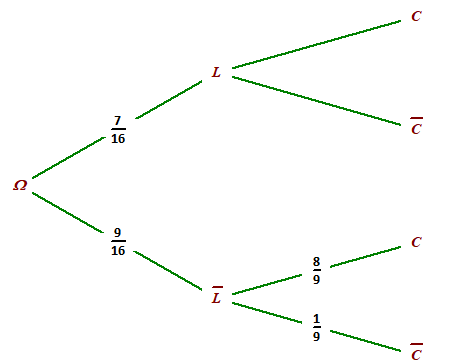
Les événements L et \(\overline{L}\) sont des événements contraires
donc
\(p(L)+p(\overline{L})=1\)
\(\iff p(\overline{L})=1-p(L)\)
or \(p(L)=\frac{7}{16}\)
donc \(p(\overline{L})=1-\frac{7}{16}=\frac{16}{16}-\frac{7}{16}=\)\(\frac{9}{16}\)
D'après l'énoncé \(p_{\overline{L}}(C)=\frac{8}{9}\)
Les événements C sachant \(\overline{L}\) et \(\overlie{C}\) sachant \(\overline{L}\)sont des événements qui forment une partition de \(\overline{L}\)
donc
\(p_{\overline{L}}(C)+p_{\overline{L}}(\overline{C})=1\)
\(\iff p_{\overline{L}}(\overline{C})=1-\frac{8}{9}=\frac{9}{9}-\frac{8}{9}=\frac{1}{9}\)
Question
2. Quelle est la probabilité qu'aucun des deux enfants ne coiffe de couronne ?
Solution
\(p(\overline{L} \cap \overline{C})=p(\overline{L}) \times p_{\overline{L}}(\overline{C})\)
\(\iff p(\overline{L} \cap \overline{C})=\frac{9}{16} \times \frac{1}{9}=\frac{1}{16}\)
Question
3. Le père calcule que la probabilité pour que son fils seul soit roi est égale
à \(\frac{3}{16}\).
En déduire que \(p_L(\overline{C}) = \frac{3}{7}\).
Finir de compléter l'arbre de probabilité.
Solution
Le fils seul est roi :
\(p(L \cap \overline{C})=\frac{3}{16}\)
\(\iff p(L) \times p_L(\overline{C})=\frac{3}{16}\)
\(\iff \frac{7}{16}\times p_L(\overline{C})=\frac{3}{16}\)
\(\iff p_L(\overline{C})=\frac{\frac{3}{16}}{\frac{7}{16}}\)
\(\iff p_L(\overline{C})=\frac{3}{16} \times \frac{16}{7}\)
\(\iff p_L(\overline{C})=\frac{3}{7}\)
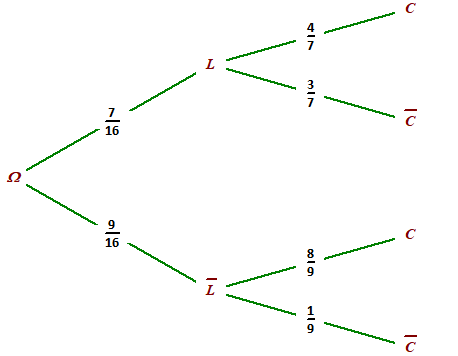
Question
4. Calculer la probabilité que Carla soit reine.
Solution
Les événements L et \(\overline{L}\) forment une partition de l'univers donc :
\(p(C)=p(L \cap C)+p(\overline{L} \cap C)\)
\(\iff p(C)=p(L) \times p_{L}(C)+p(\overline{L}) \times p_{\overline{L}}(C)\)
\(\iff p(C)=\frac{7}{16} \times \frac{4}{7}+\frac{9}{16} \times \frac{8}{9}\)
\(\iff p(C)=\frac{4}{16} +\frac{8}{16}\)
\(\iff p(C)=\frac{1}{4} +\frac{1}{2}\)
\(\iff p(C)=\frac{1}{4} +\frac{2}{4}\)
\(\iff p(C)=\frac{3}{4}\)
Question
5. Calculer \(p(\overline{C}).\)
Solution
Les événements C et \(\overline{C}\) sont des événements contraires donc :
\(p(C)+ p( \overline{C})=1\)
donc
\(p( \overline{C})=1-p(C)\)
\(\iff p( \overline{C})=1-\frac{3}{4}=\frac{4}{4}-\frac{3}{4}=\)\(\frac{1}{4}\)
Question
6. Donner la signification par une phrase de la probabilité conditionnelle \(p_C(L)\) puis calculer sa valeur
Solution
\(p_C(L)\) représente la probabilité que Louis soit roi sachant que Carla est reine.
Par la formule des probabilités conditionnelles :
\(p_C(L)=\frac{p(L \cap C)}{p(C)}\)
\(\iff p_C(L)=\frac{p(L) \times p_L(C)}{p(C)}\)
\(\iff p_C(L)=\frac{\frac{7}{16} \times \frac{4}{7}}{\frac{3}{4}}\)
\(\iff p_C(L)=\frac{\frac{4}{16}}{\frac{3}{4}}\)
\(\iff p_C(L)=\frac{4}{16} \times \frac{4}{3}\)
\(\iff p_C(L)=\frac{16}{48}=\frac{1}{3}\)
La probabilité que Louis soit roi sachant que Carla est reine est \(\frac{1}{3}\)
Question
7. Décrire par une phrase l'événement \(L \cup C\) puis en calculer la probabilité.
Solution
L'événement \(L \cup C\) représente l'événement Louis est roi ou Carla est reine ou éventuellement Louis et Carla sont roi et reine.
\(p(L \cap C)=p(L) \times p_{L}(C)\)
\(\iff p(L \cap C)=\frac{7}{16} \times \frac{4}{7}\)
\(\iff p(L \cap C)=\frac{1}{4}\)
\(p(L \cup C)=p(L)+p(C)-p(L \cap C)=\frac{7}{16}+\frac{3}{4}-\frac{1}{4}\)
\(\iff p(L \cup C)=p(L)+p(C)-p(L \cap C)=\frac{7}{16}+\frac{12}{16}-\frac{4}{16}\)
\(\iff p(L \cup C)=p(L)+p(C)-p(L \cap C)=\frac{15}{16}\)
Exercice 2
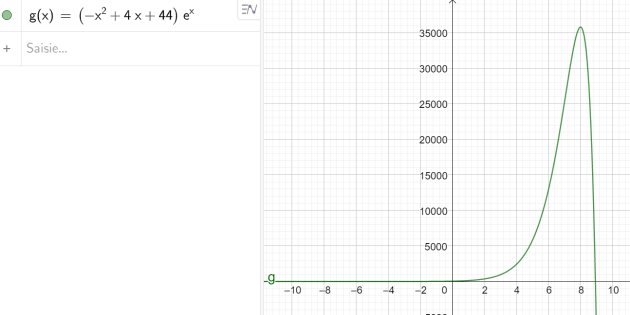
On appelle \(g\) la fonction définie sur \(\mathbb{R}\)
par \(g(x)=(-x^{2}+4x+44)e^{x}.\)
Question
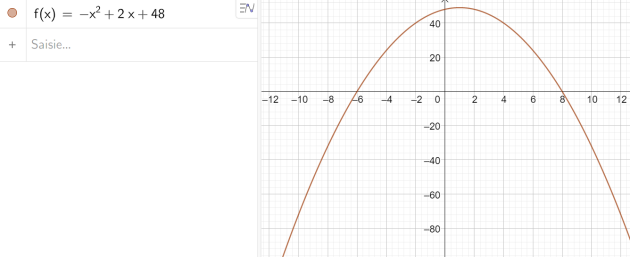
1. Montrer que \(g'(x)=(-x^{2}+2x+48)e^{x}\)
Solution
\(g'(x)=(-2x+4)e^{x}+(-x^{2}+4x+44)e^{x}\)
\(\iff g'(x)=(-x^{2}+2x+48 )e^{x}\)
Question
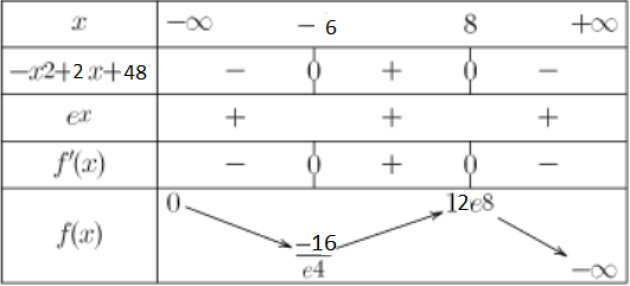
2. En déduire le signe de \(g'(x)\) puis les variations de la fonction \(g\).
On dressera un tableau de variations de la fonction \(g\).
On pourra utiliser le graphique de la fonction représenté avec le logiciel Geogebra.
Solution
\(-x^{2}+2x+48\)
\(a=-1 ;b=2 ;c=48\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=b^2-4ac\)
\(\iff \Delta=2^2-4 \times (-1) \times 48\)
\(\iff \Delta=4+192\)
\(\iff \Delta=196\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-2-\sqrt{196}}{2 \times (-1)}\\x_2=\frac{-2+\sqrt{196}}{2 \times (-1)}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-2-14}{-2}\\x_2=\frac{-2+14}{-2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-16}{-2}\\x_2=\frac{12}{-2}\end{cases}\)
\(\iff \begin{cases}x_1=8\\x_2=-6\end{cases}\)
\(g(8)=(-8^{2}+4\times 8+44)e^{8}=(-64+32+44)e^{8}=12e^{8}\)
\(g(-6)=(-(-6)^{2}+4\times (-6)+44)e^{-4}=(-36-24+44)e^{-4}=(-16)e^{-4}\)
\(\iff g(-6)=\frac{-16}{e^4}\)
Exercice 3
Un centre de loisirs destiné aux jeunes de 11 ans à 18 ans compte 40% de collégiens et 60% de lycéens.
Le directeur a effectué une étude statistique sur la possession de téléphones portables.
Cette étude a montré que 80% des jeunes possèdent un téléphone portable et que, parmi les collégiens, 70% en possèdent un.
On choisit au hasard un jeune du centre de loisirs et on s'intéresse aux événements suivants :
C : "le jeune choisi est un collégien" ;
L : "le jeune choisi est un lycéen" ;
T : "le jeune choisi possède un téléphone portable"
Question
1. Donner les probabilités : \(p(C),p(L),p(T),p_C(T).\)
Solution
\(p(C) =\frac{40}{100}=0,4\)
\(p(L) =\frac{60}{100}= 0,6\)
\(p(T) =\frac{80}{100}= 0,8\)
\(p_C(T) =\frac{70}{100}\)
Question
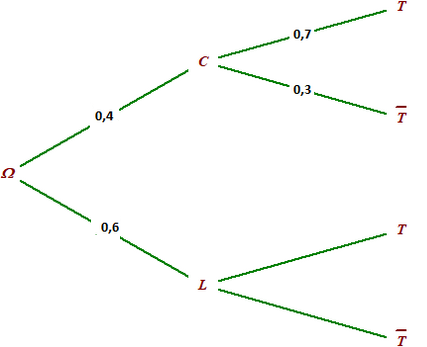
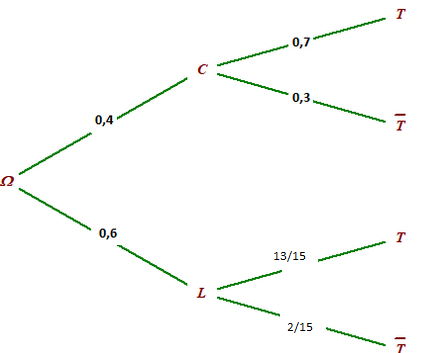
2.Faire un arbre de probabilités représentant la situation et commencer à la renseigner avec les données de l'énoncé.
Question
3. Calculer la probabilité que le jeune choisi soit un collégien possédant un téléphone portable.
Solution
D'après la définition des probabilités conditionnelles, on a :
\(p_C(T) =\frac{p(C \cap T)}{p(C)}\)
\(0,7 =\frac{p(C \cap T)}{0,4}\)
\(\iff p(C \cap T ) = 0, 7 \times 0,4\)
\(\iff p(C \cap T) = 0,28\)
Question
4.Calculer la probabilité que le jeune choisi soit un collégien sachant qu'il possède un téléphone portable.
Solution
\(p_T(C)=\frac{p(T \cap C)}{p(T)}\)
\(\iff p_T(C)=\frac{0,28}{0,8}0\)
\(\iff p_T(C)=\frac{28}{80}=\frac{7}{20}\)
\(\iff p_T(C)= 0,35\)
Question
5.a. Calculer \(p(T \cap L)\), en déduire \(p_L(T)\).
Solution
Les deux événements C et L forment une partition de l'univers :
\(C \cap L= ∅\) : un jeune ne peut être un collégien et un lycéen en même temps;
\(C \cup L= Ω\)
D'après la formule des probabilités totales, on a :
\(p(T) =p(C \cap T) + p(L \cap T)\)
\(0,8 = 0,28 + p(L \cap T)\)
donc \(p(L \cap T) = 0,8-0,28=0,52\)
D'après la définition des probabilités conditionnelles, on a :
\(p_L(T) =\frac{p(L \cap T)}{p(L)}\)
\(\iff p_L(T) =\frac{0,52}{0,6}\)
\(\iff p_L(T) =\frac{52}{60}=\frac{13}{15}\)
Question
b.Compléter l'arbre construit dans la question 2.