Exercice : Exercice 1 :
En prévision de l'Euro de Football du 11 juin au 11 juillet 2021,
un magasin d'électroménager s'intéresse au comportement d'un acheteur potentiel
d'une télévision et d'une barre de son.
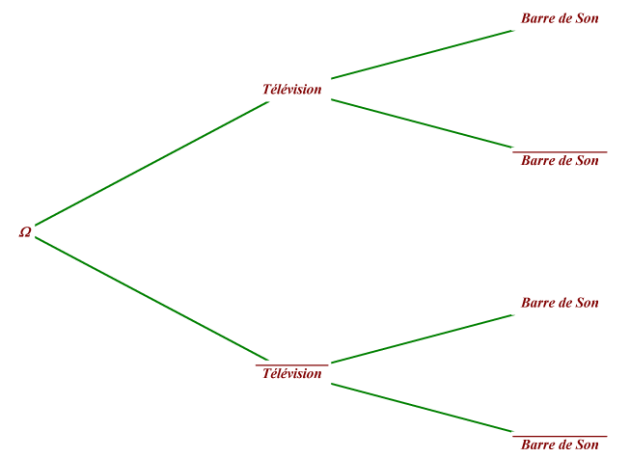
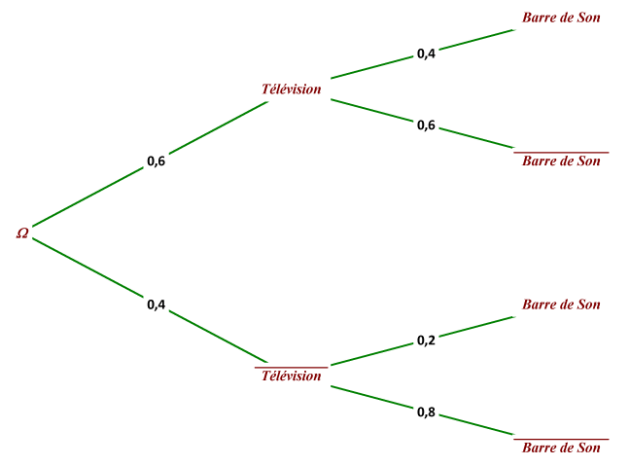
La probabilité pour qu'il achète une télévision est de 0,6.
La probabilité pour qu'il achète une barre de son quand il a acheté une télévision est de 0,4.
La probabilité pour qu'il achète une barre de son quand il n'a pas acheté de télévision est de 0,2.

Question
Question
2. Calculer la probabilité pour qu'un client achète une télévision et une barre de son ?
Solution
\(p(T \cap B)=p(T) \times p_{T}(B)=0,6 \times 0,4=0,24\)
la probabilité pour qu'un client achète une télévision et une barre de son est de 0,24
Question
3. Calculer la probabilité pour qu'un client achète une barre de son ?
Solution
D'après la formule des probabilités totales :
\(p(B)=p(B \cap T)+p(B \cap \overline{T})\)
\(\iff p(B)=p(T) \times p_{T}(B)+p(\overline{T}) \times p_{\overline{T}}(B)\)
\(\iff p(B)=0,6 \times 0,4+0,4 \times 0,2\)
\(\iff p(B)=0,24+0,08\)
\(\iff p(B)=0,32\)
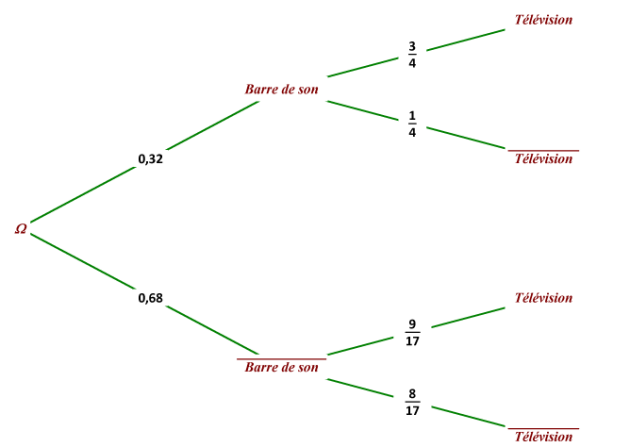
La probabilité pour que le client achète une barre de son est de 0,32
Question
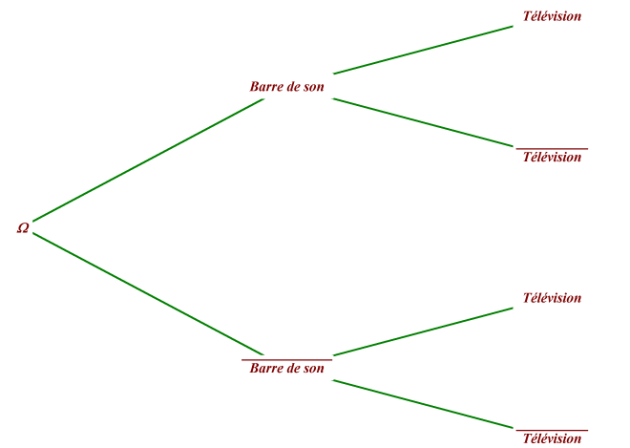
4. Le client achète une barre de son. Quelle est la probabilité qu'il achète une télévision ?
Solution
\(p_{B}(T)=\frac{p(B \cap T)}{p(B)}\)
\(\iff p_{B}(T)=\frac{0,24}{0,32}=\frac{24}{32}\)
\(\iff p_{B}(T)=\frac{3}{4}\)
Question
5. Le client n'achète pas de barre de son. Quelle est la probabilité qu'il achète une télévision ?
Solution
\(p_{\overline{B}}(T)=\frac{p(\overline{B} \cap T)}{p(\overline{B})}\)
\(\iff p_{\overline{B}}(T)=\frac{0,6 \times 0,6}{1-0,32}\)
\(\iff p_{B}(T)=\frac{0,36}{0,68}=\frac{36}{68}=\frac{18}{34}=\frac{9}{17}\)
Le client n'achète pas de barre de son, la probabilité qu'il achète une télévision est de \(\frac{9}{17}\)