Exercice : Trigonométrie
Partie A
Sur la figure ci-dessous, les points A et B du cercle trigonométrique
sont tels que \(x_A = y_B =\frac{1}{2}\).
Le point C a pour coordonnées (0;-1).
La figure est tracée dans un repère orthonormé \((0;\vec{i} ;\vec{j})\)
1. Déterminer les mesures principales des angles orientés
Question
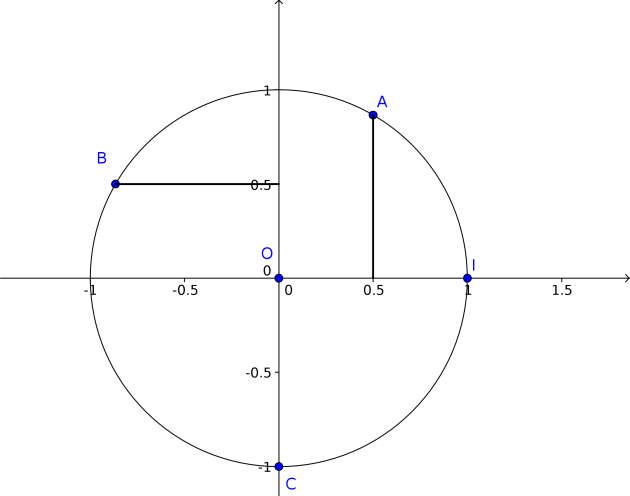
a.\((\vec{i} ;\vec{OA})\)
Solution
Comme \(x_A=cos((\vec{i} ;\vec{OA}))=\frac{1}{2}\) et \(y_A=sin((\vec{i} ;\vec{OA}))>0\)
on en déduit que \((\vec{i} ;\vec{OA})=\frac{\pi}{3}\)
Question
\(b. (\vec{i} ;\vec{OB})\)
Solution
Comme \(x_B=sin((\vec{i} ;\vec{OB}))<0\) et \(y_B=sin((\vec{i} ;\vec{OB}))=\frac{1}{2}\)
on en déduit que \((\vec{i} ;\vec{OB})=\pi-\frac{\pi}{6}=\frac{6\pi}{6}-\frac{\pi}{6}=\frac{5\pi}{6}\)
Question
\(c. (\vec{i} ;\vec{OC})\)
Solution
Comme \(x_C=cos((\vec{i} ;\vec{OC}))=0\) et \(y_C=sin((\vec{i} ;\vec{OC}))=-1\)
on en déduit que \((\vec{i} ;\vec{OC})=\frac{-\pi}{2}\)
2. Grâce à la relation de Chasles, en déduire les mesures principales des angles orientés
Question
a. \((\vec{OA} ;\vec{OB})\)
Solution
\((\vec{OA} ;\vec{OB})\)
\(=(\vec{OA} ;\vec{i})+ (\vec{i} ;\vec{OB})\)
\(=-(\vec{i} ;\vec{OA})+ (\vec{i} ;\vec{OB})\)
\(=-\frac{\pi}{3}+\frac{5\pi}{6}\)
\(=-\frac{2\pi}{6}+\frac{5\pi}{6}\)
\(=\frac{3\pi}{6}=\frac{\pi}{2}\)
Question
\(b. (\vec{OB} ;\vec{OC})\)
Solution
\((\vec{OB} ;\vec{OC})\)
=\((\vec{OB} ;\vec{i})+ (\vec{i} ;\vec{OC})\)
\(=-(\vec{i} ;\vec{OB})+ (\vec{i} ;\vec{OC})\)
\(=-\frac{5\pi}{6}+\frac{-\pi}{2}\)
\(=-\frac{5\pi}{6}-\frac{3\pi}{6}\)
\(=-\frac{8\pi}{6}=-\frac{4\pi}{3} \notin ]-\pi ;\pi]\)
\(=-\frac{4\pi}{3}+2\pi=-\frac{4\pi}{3}+\frac{6\pi}{3}=\frac{2\pi}{3} \in ]-\pi ;\pi]\)
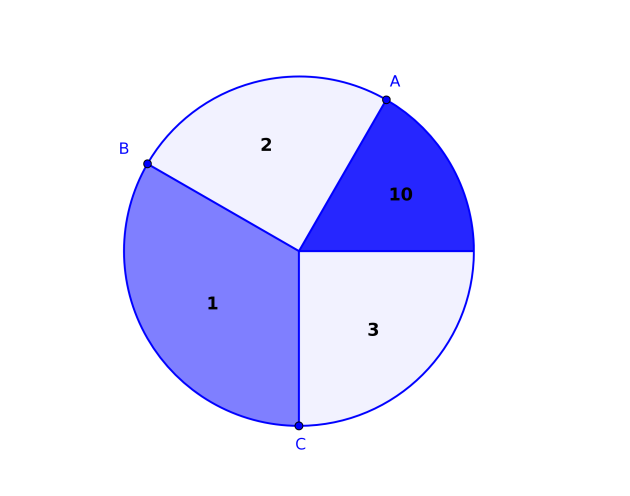
On considère maintenant le cercle trigonométrique comme une cible découpée en quatre secteurs
comme sur la figure ci-dessous.
Chaque secteur est marqué d'un nombre de points : 10, 2, 1 ou 3.
Un tir sur la cible est considéré comme une expérience aléatoire
dont l'issue est l'atteinte d'un des quatre secteurs.
La probabilité qu'un secteur soit atteint est proportionnelle à l'aire de ce secteur.
1. On effectue un tir et on appelle R la variable aléatoire prenant
pour valeur le nombre de points marqué sur le secteur atteint.
Question
a.Reproduire et compléter le tableau ci-dessous.
\(r_i\) | 1 | 2 | 3 | 10 |
|---|---|---|---|---|
\(p(R = r_i)\) |
Solution
\(r_i\) | 1 | 2 | 3 | 10 |
|---|---|---|---|---|
\(p(R = r_i)\) | \(|\frac{(\vec{OB} ;\vec{OC})}{2\pi}|=\frac{\frac{2\pi}{3}}{2\pi}= \frac{1}{3}\) | \(|\frac{((\vec{OA} ;\vec{OB}))}{2\pi}|=\frac{\frac{\pi}{2}}{2\pi}= \frac{1}{4}\) | \(|\frac{(\vec{i} ;\vec{OC})}{2\pi}|=|\frac{\frac{-\pi}{2}}{2\pi}|= \frac{1}{4}\) | \(|\frac{((\vec{i} ;\vec{OA})}{2\pi}|=\frac{\frac{\pi}{3}}{2\pi}=\frac{1}{6}\) |
\(\color{red}{\text{Pensez à vérifier que le tableau est bien un tableau de loi de probabilités}}\)
\(\frac{1}{3}+\frac{1}{4}+\frac{1}{4}+\frac{1}{6}\)
=\(\frac{4}{12}+\frac{3}{12}+\frac{3}{12}+\frac{2}{12}\)
=\(\frac{12}{12}=1\)
Le tableau est donc bien un tableau de loi de probabilités.
Question
b.Calculer l'espérance mathématique de la variable aléatoire R.
Solution
\(E(R)=\sum_{i=1}^{n} r_i \times p(R=r_i)\)
\(\iff E(R)=1 \times \frac{1}{3}+2\times \frac{1}{4}+3 \times \frac{1}{4}+10\times \frac{1}{6}\)
\(\iff E(R)=\frac{1}{3}+\frac{1}{2}+\frac{3}{4}+\frac{5}{3}\)
\(\iff E(R)=\frac{4}{12}+\frac{6}{12}+\frac{9}{12}+\frac{20}{12}\)
\(\iff E(R)=\frac{39}{12}=\frac{13}{4}=3,25\)
Question
c.Calculer la variance et l'écart type mathématique de la variable aléatoire R.
Solution
Calcul de la variance :
\(V(R)=\sum_{i=1}^{n} (r_i-E(R))^2 \times p(R=r_i)\)
\(\iff V(R)=(1-\frac{13}{4})^2 \times \frac{1}{3}+(2-\frac{13}{4})^2 \times \frac{1}{4}+(3-\frac{13}{4})^2 \times \frac{1}{4}+(10-\frac{13}{4})^2 \times \frac{1}{6}\)
\(\iff V(R)=(\frac{4}{4}-\frac{13}{4})^2 \times \frac{1}{3}+(\frac{8}{4}-\frac{13}{4})^2 \times \frac{1}{4}+(\frac{12}{4}-\frac{13}{4})^2 \times \frac{1}{4}+(\frac{40}{4}-\frac{13}{4})^2 \times \frac{1}{6}\)
\(\iff V(R)=(\frac{9}{4})^2 \times \frac{1}{3}+(-\frac{5}{4})^2 \times \frac{1}{4}+(-\frac{1}{4})^2 \times \frac{1}{4}+(\frac{27}{4})^2 \times \frac{1}{6}\)
\(\iff V(R)=\frac{81}{16} \times \frac{1}{3}+\frac{25}{16} \times \frac{1}{4}+\frac{1}{16} \times \frac{1}{4}+\frac{729}{16} \times \frac{1}{6}\)
\(\iff V(R)=\frac{27}{16}+\frac{25}{64}+\frac{1}{64}+\frac{243}{32}\)
\(\iff V(R)=\frac{108}{64}+\frac{25}{64}+\frac{1}{64}+\frac{486}{64}\)
\(\iff V(R)=\frac{620}{64}=\frac{310}{32}=\frac{155}{16}\)
Calcul de l'écart type :
\(\sigma(R)=\sqrt{V(R)}=\sqrt{\frac{155}{16}}=\frac{\sqrt{155}}{4}\)
Calcul de l'intervalle de forte probabilité:
\([E(R)-\sigma(R) ;E(R)+\sigma(R)]=[\frac{13}{4}-\frac{\sqrt{155}}{4} ;\frac{13}{4}+\frac{\sqrt{155}}{4}]\)
\(\iff [E(R)-\sigma(R) ;E(R)+\sigma(R)]=[\frac{13-\sqrt{155}}{4} ;\frac{13+\sqrt{155}}{4}]\)
\(\iff [E(R)-\sigma(R) ;E(R)+\sigma(R)]=[\frac{13-\sqrt{155}}{4} ;\frac{13+\sqrt{155}}{4}]\)
\(\iff [E(R)-\sigma(R) ;E(R)+\sigma(R)]\simeq[0,14 ;6,36]\)
\(\color{magenta}{\text{Les gains dans ce jeu ont de fortes chances de se trouver}}\)
\(\color{magenta}{\text{en moyenne sur un grand nombre de parties entre 0,14 point et 6,36 points.}}\)