Exercice : Calcul d'angles
Dans le plan muni d'une base orthonormale \((O ;\vec{i} ;\vec{j})\),
on considère les vecteurs
\(\vec{u}=-2\vec{i}+\vec{j}\) et et \(\vec{v}= 5\vec{i}+ 2\vec{j}\)
Question
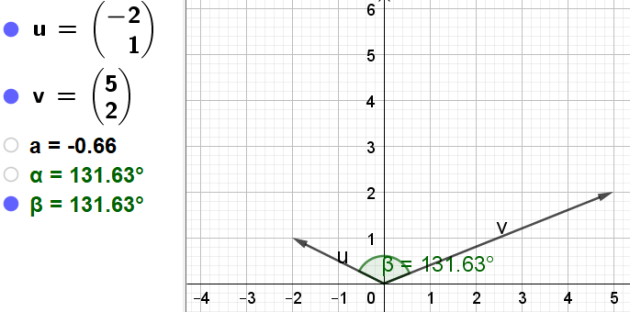
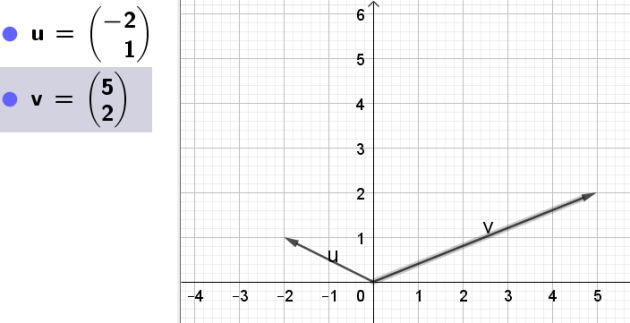
1. Représenter \(\vec{u}\) et \(\vec{v}\)
2. Calculer les valeurs exactes de :
Question
a.\(||\vec{u}||\)
Solution
\(||\vec{u}||=\sqrt{(-2)^2+1^2}\)
\(\iff ||\vec{u}||=\sqrt{4+1}=\sqrt{5}\)
Question
b.\(||\vec{v}||\)
Solution
\(||\vec{v}||=\sqrt{5^2+2^2}\)
\(\iff ||\vec{v}||=\sqrt{25+4}=\sqrt{29}\)
Question
c. \(\vec{u}.\vec{v}\)
Solution
\(\vec{u}.\vec{v}=xx'+yy'\)
\(\iff \vec{u}.\vec{v}=(-2) \times 5+1 \times 2\)
\(\iff \vec{u}.\vec{v}=-10+2=-8\)
Question
3. En déduire une valeur approchée à \(10^{-2}\) près de la mesure principale, en degré,
de l'angle orienté \((\vec{u} ;\vec{v})\).
Solution
\(\vec{u}.\vec{v}=||\vec{u}||.||\vec{v}||.cos((\vec{u},vec{v}))\)
\(\iff -8=\sqrt{5}.\sqrt{29}.cos((\vec{u},vec{v}))\)
\(\iff cos((\vec{u},\vec{v}))=\frac{-8}{\sqrt{5}.\sqrt{29}}\)
\(\iff (\vec{u},\vec{v})=Arccos(\frac{-8}{\sqrt{5}.\sqrt{29}})\)
\(\iff (\vec{u},\vec{v})=Arccos(\frac{-8}{\sqrt{5}.\sqrt{29}})\)
\(\iff (\vec{u},\vec{v})\simeq-131,63°\)