Exercice : Second Degré
On considère les deux fonctions du second degré \(f\) et \(g\),
définies respectivement par
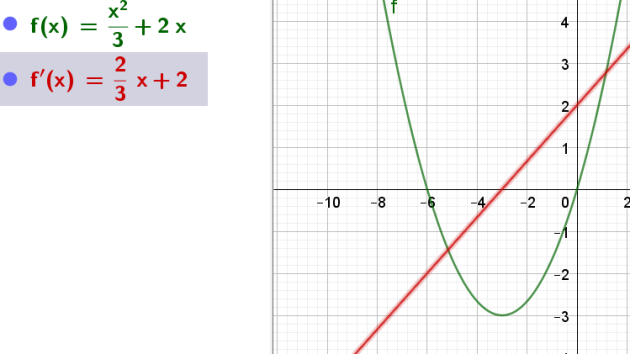
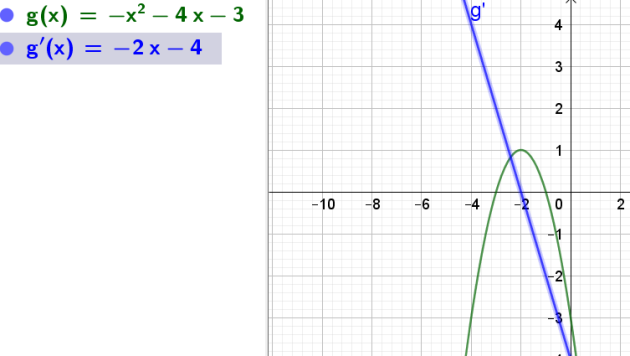
\(f (x) = \frac{x^2}{3}+2x\) et \(g(x) = -x^2 - 4x - 3\)
Vous pourrez contrôler la vraisemblance de vos résultats à l'aide de Géogebra
Question
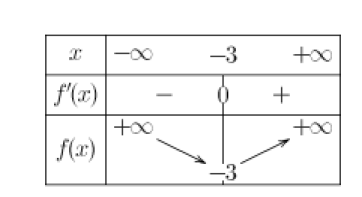
1. Donner, en les justifiant, les tableaux de variations respectifs des fonctions \(f\) et \(g\).
Solution
\(\color{magenta}{\text{1ère méthode : Par dérivation}}\)
\(f (x) = \frac{x^2}{3}+2x\)
\(f'(x) = \frac{2x}{3}+2\)
\(f'(x) = \frac{2x}{3}+2=0\)
\(\iff \frac{2x}{3}+2=0\)
\(\iff \frac{2x}{3}=-2\)
\(\iff 2x=-2 \times 3\)
\(\iff 2x=-6\)
\(\iff x=-3\)
\(f (-3) = \frac{(-3)^2}{3}+2\times (-3)\)
\(\iff f (-3) = \frac{9}{3}-6\)
\(\iff f (-3) = 3-6=-3\)
le sommet de la parabole correspondant à la fonction \(f\) a pour sommet le point de coordonnées (-3 ;-3)
\(g(x) = -x^2 - 4x - 3\)
\(g'(x) = -2x - 4\)
\(g'(x) = -2x - 4=0\)
\(\iff -2x - 4=0\)
\(\iff -2x =4\)
\(\iff x =\frac{4}{-2}=-2\)
\(g(-2) = -(-2)^2 - 4 \times (-2)- 3\)
\(\iff g(-2) = -4 +8- 3=1\)
le sommet de la parabole correspondant à la fonction \(g\) a pour sommet le point de coordonnées (-2 ;1)
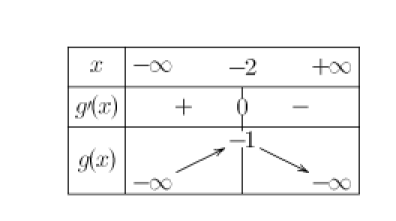
\(\color{magenta}{\text{2ème méthode : Par calcul des coordonnées du sommet des paraboles}}\)
\(f (x) = \frac{x^2}{3}+2x\)
\(\alpha=\frac{-b}{2a}\)
\(\alpha=\frac{-2}{2\frac{1}{3}}\)
\(\iff \alpha=\frac{-2}{\frac{2}{3}}\)
\(\iff \alpha=-2 \times \frac{3}{2}=-3\)
\(\beta=f(\alpha)\)
\(\iff \beta=f (-3) = \frac{(-3)^2}{3}+2\times (-3)\)
\(\iff \beta= \frac{9}{3}-6\)
\(\iff \beta = 3-6=-3\)
le sommet de la parabole correspondant à la fonction \(f\) a pour sommet le point de coordonnées (-3 ;-3)
Comme le coefficient du terme en "\(x^2\)" est \(\frac{1}{3}>0\),
on en déduit que la parabole correspondante est celle d'une fonction décroissante puis croissante.
\(g(x) = -x^2 - 4x - 3\)
\(\alpha=\frac{-b}{2a}\)
\(\alpha=\frac{-(-4)}{2\times (-1)}\)
\(\iff \alpha=\frac{4}{-2}\)
\(\iff \alpha=-2\)
\(\beta=g(\alpha)\)
\(\iff \beta=g(-2) = -(-2)^2 - 4 \times (-2)- 3\)
\(\iff \beta=-4 +8- 3=1\)
le sommet de la parabole correspondant à la fonction \(g\) a pour sommet le point de coordonnées (-2 ;1)
Comme le coefficient du terme en "\(x^2\)" est \(-1<0\),
on en déduit que la parabole correspondante est celle d'une fonction croissante puis décroissante.
Question
2. Sur le graphique ci-dessous :
quelle courbe représente la fonction \(f\) ?
quelle courbe représente la fonction \(g\) ?
Justifier votre choix.
Solution
D'après la question précédente,
le sommet de la parabole correspondant à la fonction \(f\) a pour sommet le point de coordonnées (-3 ;-3)
ce qui est le cas pour la parabole représentée en rouge.
De plus la fonction représentée par la parabole rouge est croissante puis décroissante donc son coefficient du terme en "\(x^2\)" est positif
ce qui est le cas pour la fonction \(f\) et non pour la fonction \(g\).
le sommet de la parabole correspondant à la fonction \(g\) a pour sommet le point de coordonnées (-2 ;1) ce qui est le cas pour la parabole représentée en violet.
De plus la fonction représentée par la parabole violette est décroissante puis croissante donc son coefficient du terme en "\(x^2\)" est négatif
ce qui est le cas pour la fonction \(g\) et non pour la fonction \(f\).
Question
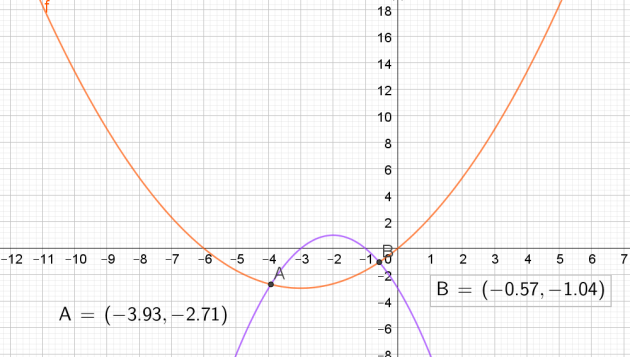
3. Calculer les solutions de l'équation \(f (x) = g (x)\)
Solution
\(f(x)=g(x)\)
\(\iff \frac{x^2}{3}+2x=-x^2-4x-3\)
\(\iff \frac{x^2}{3}+2x+x^2+4x+3=0\)
\(\iff \frac{x^2}{3}+x^2+6x+3=0\)
\(\iff \frac{x^2}{3}+\frac{3x^2}{3}+6x+3=0\)
\(\iff \frac{x^2}{3}+\frac{3x^2}{3}+6x+3=0\)
\(\iff \frac{4x^2}{3}+6x+3=0\) (\(E_1\))
\(\iff 4x^2+18x+9=0\) (\(E_1 \times 3)\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=18^2-4 \times 4 \times 9\)
\(\iff \Delta=324-144\)
\(\iff \Delta=180\)
Comme \(\Delta>0\), l'équation \(f(x) =g(x)\) admet deux solutions
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-18-\sqrt{180}}{2 \times 4}\\x_2=\frac{-18+\sqrt{180}}{2 \times 4}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-18-\sqrt{36\times 5}}{8}\\x_2=\frac{-18+\sqrt{36\times 5}}{8}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-18-6\sqrt{5}}{8}\\x_2=\frac{-18+6\sqrt{5}}{8}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-9-3\sqrt{5}}{4}\\x_2=\frac{-9+3\sqrt{5}}{4}\end{cases}\)
Question
4.Déterminer l'ensemble des solutions de l'inéquation \(g(x) > f(x)\)
Solution
\(g(x)>f(x)\)
\(\iff -x^2-4x-3>\frac{x^2}{3}+2x\)
\(\iff 0>\frac{x^2}{3}+2x+x^2+4x+3\)
\(\iff 0>\frac{x^2}{3}+x^2+6x+3\)
\(\iff 0>\frac{4x^2}{3}+6x+3\)
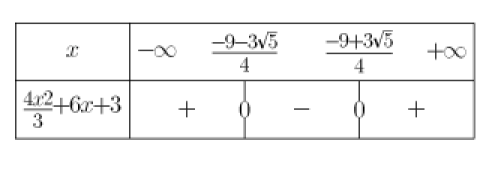
\(g(x)>f(x) \iff x\in] ;\frac{-9-3\sqrt{5}}{4}\frac{-9+3\sqrt{5}}{4}[\)