Exercice : Fonction carrée
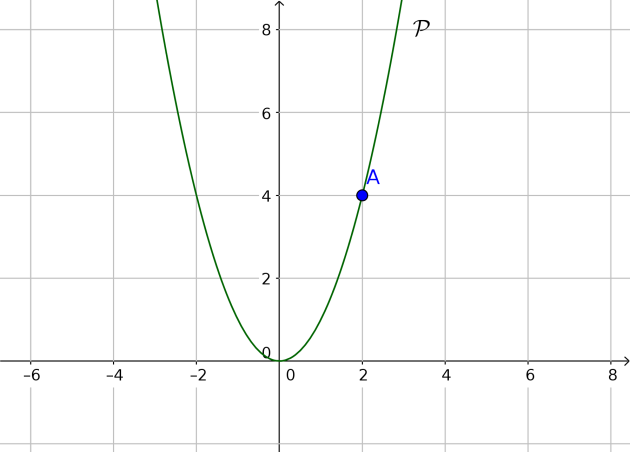
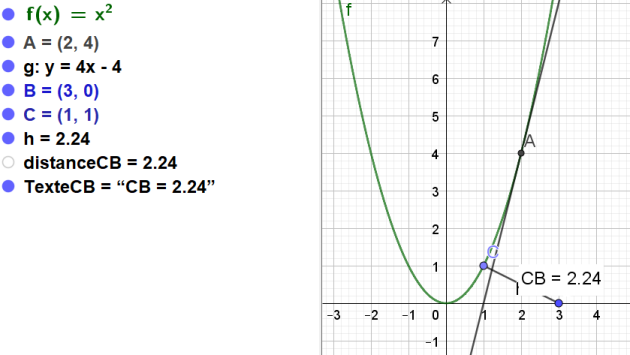
Dans un repère orthonormé du plan, on considère la parabole P
représentant la fonction carrée définie, pour tout nombre réel \(x\) par :
\(\phi(x) = x^2\).
Le point A, dont l'abscisse est 2, appartient à la parabole P.
Partie A
.
Question
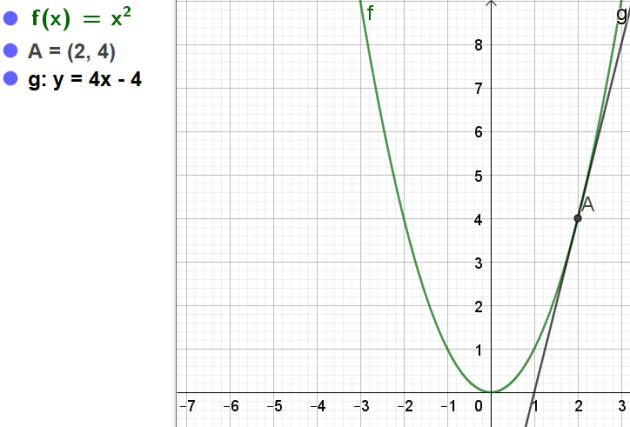
1. Sur la figure ci-dessous, construire la droite (D) passant par le point A de coefficient directeur 4.
Calculer une équation réduite puis une équation cartésienne de cette droite.
Indice
L'équation d'une droite sous forme réduite est
de la forme \(y=ax+b\)
\(\color{red}{\text{L'équation réduite d'une droite est unique,}}\)
Une équation d'une droite sous forme cartésienne est
de la forme \(ax+by+c=0\)
\(\color{red}{\text{Une équation cartésienne d'une droite n'est pas unique,}}\)
\(\color{red}{\text{on peut multiplier tous les coefficients par un même nombre.}}\)
Solution
La droite de coefficient directeur 4 et passant par le point A admet une équation de la forme :
\(y=4x+b\)
or \(A(2,f(2))\in(D)\)
\(\iff A(2,2^2)\in(D)\)
\(\iff A(2,4)\in(D)\)
\(\iff 4=4 \times 2+b\)
\(\iff 4=8+b\)
\(\iff 4-8=b\)
\(\iff b=4-8=-4\)
L'équation réduite de la droite (D) est donc \(y=4x-4\)
Une équation cartésienne de la droite (D) est donc :
\(y-4x+4=0\) (Equation 1)
Une autre équation cartésienne de la droite (D) pourrait être \(2y-8x+8=0\) (Equation 1 \(\times 2\)) par exemple.
Question
2. a.Résoudre l'équation
\(x^2 = 4x − 4\)
Solution
\(x^2 = 4x − 4\)
\(\iff x^2-4x+4=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-4)^2-4 \times 1 \times 4\)
\(\iff \Delta=16-16\)
\(\iff \Delta=0\)
Comme \(\Delta=0\), l'équation \(x^2 = 4x − 4\) admet une seule solution.
\(x_0=-\frac{b}{2a}=-\frac{-4}{2\times 1}\)
\(\iff x_0=-\frac{-4}{2}=2\)
Question
b. Combien la droite (D) et la parabole P ont-elles de points d'intersection ?
Solution
De la question précédente, on déduit que parabole représentant la fonction \(x \mapsto x^2\) et la droite (D) d'équation \(y=4x-4\)
ont un unique point d'intersection,
il s'agit du point de coordonnées \((2,f(2))=(2,2^2)=(2,4)\) et il s'agit donc du point A.
Remarque :
On retrouve la valeur 4 de l'ordonnée du point en utilisant l'équation de le droite (D)
\(y=4 \times 2-4=8-4=4\)
Question
3.Déterminer l'équation de la tangent à la parabole P au point A par le calcul.
En déduire que D est bien la tangente à la parabole P au point A.
Solution
L'équation de la tangente à la parabole P au point A(2,4)
est de la forme :
\(y=\phi'(a)(x-a)+\phi(a)\)
\(\iff y=\phi'(2)(x-2)+\phi(2)\)
\(\phi(x)=x^2 \)sur \(\mathbb{R}\) \(\mapsto \phi'(x)=2x\) sur \(\mathbb{R}\)
\(\iff y=2 \times 2 \times (x-2)+2^2\)
\(\iff y=4 \times (x-2)+4\)
\(\iff y=4x-8+4=4x-4\)
L'équation de la tangente à la fonction \(\phi\) au point A
et l'équation de la droite (D) sont donc identiques.
On en déduit que (D) est donc bien la tangente à la parabole (P) au point A.
Partie B
On considère le point B de coordonnées (3 ; 0).
Soit M un point de la parabole P d'abscisse \(x\)
Question
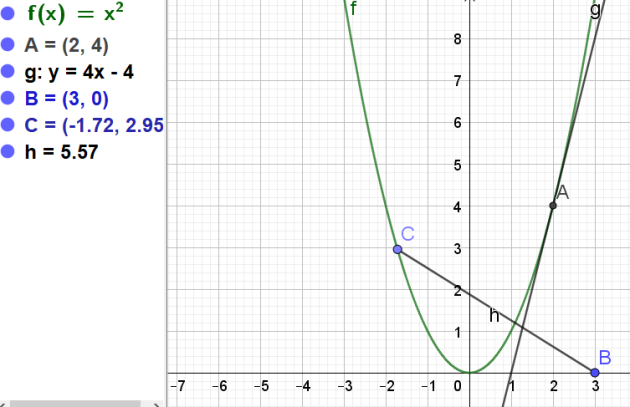
1.Donner l'expression de la distance BM en fonction de \(x\)
Solution
\(BM=\sqrt{(x_M-x_B)^2+(y_M-y_B)^2}\)
\(\iff BM=\sqrt{(x-3)^2+(\phi(x)-0)^2}\)
\(\iff BM=\sqrt{(x-3)^2+(x^2-0)^2}\)
\(\iff BM=\sqrt{x^2-2 \times x \times 3 + 3^2+(x^2)^2}\)
\(\iff BM=\sqrt{x^2-6x + 9+x^4}\)
\(\iff BM=\sqrt{x^4+x^2-6x + 9}\)
Question
2. Etudier les variations de la fonction \(f(x)=BM^2\),
en dressant un tableau de signes de \(f'(x)\) selon les valeurs de \(x\)
en déduire l'abscisse du point M de la parabole P pour lequel la distance entre les points B et M est minimale.
Indice
Montrer que \(f'(x)\) se factorise en \(2(x-1)(2x^2+2x+3)\)
Solution
\(BM^2=\sqrt{x^4+x^2-6x + 9}^2\)
\(\iff BM^2=x^4+x^2-6x + 9\)
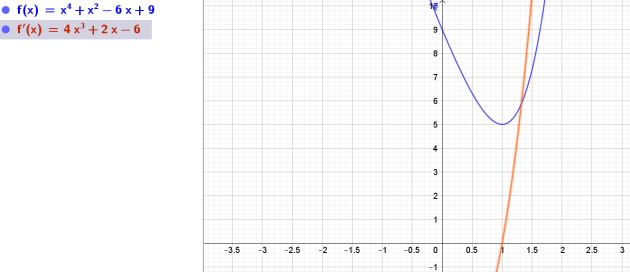
\(\iff f(x)=x^4+x^2-6x + 9\)
\(f'(x)=4x^3+2x-6\)
\(2(x-1)(2x^2+2x+3)=(2x-2)(2x^2+2x+3)\)
\(\iff 2(x-1)(2x^2+2x+3)=2x \times 2x^2 + 2x \times 2x +2x \times 3-4x^2-4x-6\)
\(\iff 2(x-1)(2x^2+2x+3)=4x^3 +4x^2 +6x-4x^2-4x-6\)
\(\iff 2(x-1)(2x^2+2x+3)=4x^3 +2x-6\)
donc \(f'(x)=2(x-1)(2x^2+2x+3)\)
\(x-1=0\)
\(\iff x=1\)
\(2x^2+2x+3=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=2^2-4 \times 2 \times 3\)
\(\iff \Delta=4-24\)
\(\iff \Delta=-20\)
\(\Delta<0\) donc l'équation \(2x^2+2x+3=0\) n'admet pas de solution
et \(2x^2+2x+3\) est toujours du signe du coefficient du terme du second degré "\(x^2\)".
Comme ce coefficient vaut ici a=2>0, on déduit que \(2x^2+2x+3\) est toujours positif.
On en déduit le tableau de signes de \(f'\):
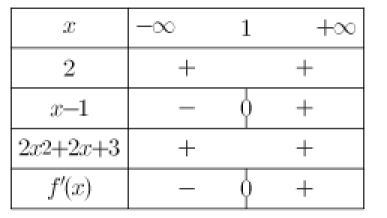
et le tableau de variations de \(f\):
\(f(1)=1^4+1^2-6\times 1+ 9\)
\(\iff f(1)=1+1-6+ 9=5\)
Graphiquement :
\(lim_{x\mapsto+\infty}f(x)=+\infty\)
\(lim_{x\mapsto-\infty}f(x)=+\infty\)
(Le terme qui l'emporte en \(-\infty\) et \(+\infty\) est le terme \(x^4\))
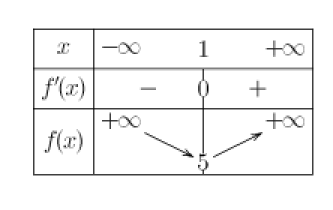
L'abscisse du point M de la parabole P pour lequel la distance entre les points B et M est minimale est le point d'abscisse \(x=1\).
Cette distance vaut alors \(\sqrt{5}\)
En effet \(BM^2=5 \iff BM=\sqrt{5}\).
