Fille ou garçon
Exemple :
\(\color{red}{\textbf{Quelques fonctions du tableur}}\)
Toute formule de calcul commence par « = » sinon le tableur pense qu'il s'agit de texte à afficher ;
A2 fait référence au contenu de la case située à l'intersection de la ligne 2 et de la colonne A ; cette référence est relative et est donc modifiée lors d'un copié collé ;
$A$2 fait référence à la même case mais c'est une référence absolue et n'est donc pas modifiée lors d'un copié collé (on peut aussi utiliser $A2 pour ne fixer que la colonne ou A$2 pour ne fixer que la ligne) ;
SI(test ; valeursivrai ; valeursifaux) renvoie valeursivrai si le test est vrai, valeursifaux sinon;
par exemple SI(A2>6 ;“youpi” ;“zut”) affiche dans la case youpi si le contenu de A2 est un nombre strictement plus grand que 6 et zut sinon;
SOMME(plage) fait la somme de tous les nombres contenus dans les cases de la plage
ENT(nombre) renvoie la partie entière du nombre ;
ALEA.ENTRE.BORNES(min; max) renvoie un nombre entier pseudo aléatoire compris entre min et max ;
NB.SI(plage ; critère) indique le nombre de cases de la plage correspondant au critère ; ainsi NB.SI(A2 : B6 ; 2) indique le nombre de 2 contenus dans les cases de la plage rectangulaire allant de A2 à B6 ;
\(\color{magenta}{\textbf{Activité à l'aide du tableur (Fille ou garçon)}}\)
J'ai rencontré en ville un ancien camarade de classe accompagné de son fils.
Il m'a donné de ses nouvelles et m'a dit qu'il avait un deuxième enfant.
Je lui ai dit : « Vous avez donc un garçon et . . . ? »
Il me répondit : « Je pense que tu ne devineras pas. Un garçon ? Une fille ?»
On suppose pour simplifier les choses qu'un enfant sur deux qui naît est une fille et l'autre un garçon.
1. Que conjecturez-vous a priori, son deuxième enfant est un fils ou une fille
2. On se propose d'utiliser la colonne :
- A pour simuler le sexe du premier enfant
- B pour celui du second enfant
- C pour compter le nombre de garçons.
Proposer des formules utilisant la fonction ALEA
Pour :
simuler le sexe d'un enfant dans les cases A1 et B1
compter le nombre de garçons de la fratrie dans la case C1.
3. Simuler 100 familles de deux enfants.
4. Dresser un tableau de la forme suivante
Nombre de garçons | 0 | 1 | 2 | Total |
|---|---|---|---|---|
Effectif |
où les cases Effectif seront automatiquement complétées par le tableur (utiliser la fonction NB.SI)
5. En appuyant plusieurs fois sur la touche F9 (Excel) ou CTRL+MAJ+F9 (Calc), indiquer autour de quels effectifs semblent osciller les types de famille.
6. Puisque l'un des enfants est un garçon, quel type de famille doit-on exclure ?
7. En observant les types de famille restants, déterminer les probabilités de trouver la bonne réponse :
si je réponds que son deuxième enfant est une fille.
si je réponds que son deuxième enfant est un garçon.
Complément :
\(\color{magenta}{\textbf{Probabilité théorique d'avoir une famille comportant deux garçons :}}\)
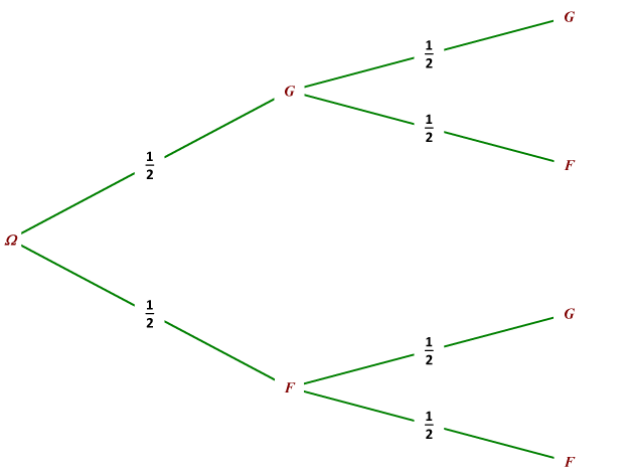
\(p(\textbf{"la famille comporte deux garçons"})=p((G,G))=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\)
\(\color{magenta}{\textbf{Probabilité théorique d'avoir une famille comportant un garçon :}}\)
\(p(\textbf{"la famille comporte deux garçons"})=p((F,G))+p((G,F))=\frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
\(\color{red}{\textbf{La probabilité est de 50% pour que la famille ne comporte que 1 garçon }}\)
\(\color{red}{\textbf{et la probabilité est de 25% pour que la famille comporte 2 garçons.}}\)
\(\color{red}{\textbf{La probabilité que j'ai raison en disant que le deuxième enfant est une fille est de 50%}}\)
\(\color{red}{\textbf{et la probabilité que j'ai raison en disant que le deuxième enfant est un garçon est de 25%}}\)
Complément :
\(\color{magenta}{\textbf{Activité Tableur : Deux dés}}\)
On lance \(\color{red}{\textbf{deux dés à six faces}}\) qu'on suppose équilibrés et on s'intéresse à la somme de deux numéros indiqués par les faces supérieures des dés.
1. Quels sont les résultats possibles ?
2. À l'aide du tableur, en vous inspirant de la façon de procéder de l'activité précédente (une colonne pour chaque dé), conjectuer, sur mille lancers, la fréquence autour de laquelle oscille chaque somme
On rappelle que la fréquence d'une valeur est l'effectif de cette valeur divisé par le total des effectifs).
3. Comment expliquer ces fréquences ? On réalisera un arbre de probabilité.
4. Calculer la probabilité d'obtenir une Somme égale à 7.