Paradoxe du Duc de Toscane
Exemple :
\(\color{magenta}{\textbf{Galilée (1554-1642)}}\) est surtout connu pour son invention de la lunette et ses travaux en astronomie.
Cependant, en 1620, alors qu'il est Premier Mathématicien de l'Université de Pise, il rédige un petit mémoire sur les jeux de dés pour répondre à une demande du Duc de Toscane.
Il est ainsi l'un des premiers avec Cardan à avoir écrit sur le « calcul des hasards », mais leurs écrits n'ont été publiés qu'après la célèbre correspondance entre Pascal et
Fermat qui marque « officiellement » le début de la théorie des probabilités.
Le mémoire de Galilée qui nous intéresse n'a été édité qu'en 1718.
A la cour de Florence, de nombreux jeux de société étaient alors pratiqués. L'un de ces jeux consistait à lancer 3 dés et à parier sur la somme des faces.
Le Duc de Toscane, qui avait sans doute observé un grand nombre de parties, avait constaté que
\(\color{red}{\textbf{la somme 10 était obtenue légèrement plus souvent que la somme 9}}\).
\(\color{magenta}{\textbf{Partie I : Simulation des lancers de trois dés }}\)
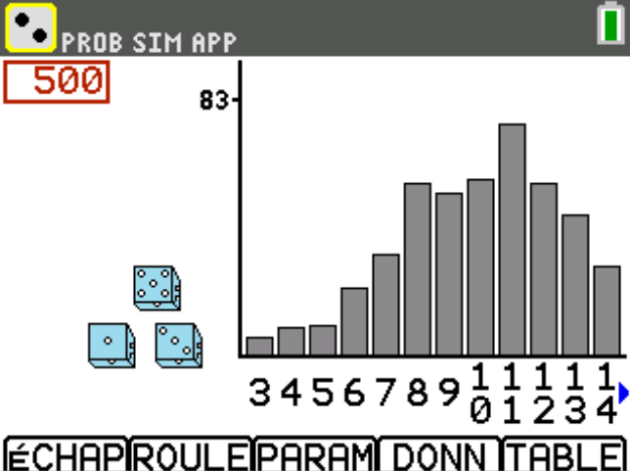
1) Simuler cette expérience à l'aide de votre calculatrice en faisant 500 lancers.
2) Recommencer plusieurs fois et noter pour chaque série les fréquences du 9 et du 10.
Série 1 | Série 2 | Série 3 | Série 4 | Série 5 | Série 6 | Série 7 | Série 8 | Moyenne | |
|---|---|---|---|---|---|---|---|---|---|
Fréquence du 9 | |||||||||
Fréquence du 10 |
\(\color{magenta}{\textbf{Partie II : Théorie : }}\)
\(\color{red}{\textbf{Le paradoxe, que le Duc avait exposé à Galilée, réside dans le fait qu'il y a autant de façons d'écrire 10 que 9 comme sommes de trois entiers compris entre 1 et 6 (6 façons).}}\)
3) Donner les décompositions possibles de ces deux nombres.
4) Quel est l'univers de cette expérience et quel est son cardinal ?
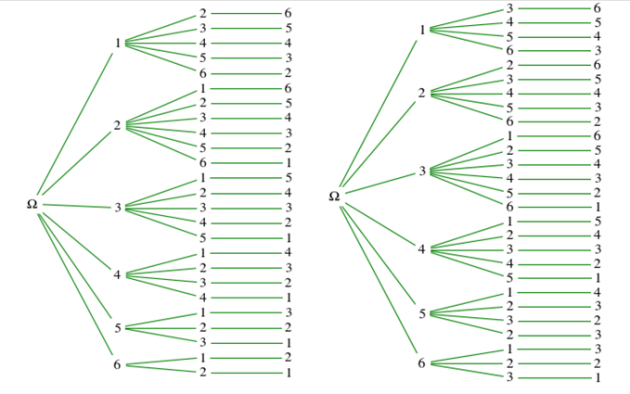
5) Faire un arbre pour déterminer combien de lancers différents permettent d'obtenir 9.
6) Quelle est la probabilité d'obtenir 9 ?
7) Faire un arbre pour déterminer combien de lancers différents permettent d'obtenir 10.
8) Quelle est la probabilité d'obtenir 10 ?w<
Complément :
Exemple de tableau obtenu :
Série 1 | Série 2 | Série 3 | Série 4 | Série 5 | Série 6 | Série 7 | Série 8 | Moyenne | |
|---|---|---|---|---|---|---|---|---|---|
Fréquence du 9 | 64 | 48 | 56 | 48 | 48 | 66 | 51 | 62 | 55,375 |
Fréquence du 10 | 67 | 63 | 70 | 66 | 62 | 56 | 69 | 65 | 64,75 |
\(\color{magenta}{\textbf{Ecriture des décompositions des nombres :}}\)
\(\fbox{9}\): 1-2-6 , 1-3-5 , 1-4-4 , 2-2-5 , 2-3-4 , 3-3-3 \(\mapsto\) 6 décompositions
\(\fbox{10}\) : 1-3-6 , 1-4-5 , 2-2-6 , 2-3-5, 2-4-4 , 3-3-4 \(\mapsto\) 6 décompositions
\(\color{red}{\textbf{Donc il y a autant de façons d'écrire 10 et 9 comme sommes de trois entiers compris entre 1 et 6 (6 façons).}}\)
3. Décomposition des nombres 9 et 10 :
4) L'univers de cette expérience est \(\Omega\)={(1,1,1),(1,1,2),(1,1,3), \(\dots\) ,(6,6,6)}
Le cardinal de \(\Omega\) est 6 issues premier lancer \(\times\) 6 issues second lancer \(\times\) 6 issues troisième lancer=\(6^3\)
6) p("obtenir 9")=\(\frac{25}{216}\)
8) p("obtenir 10")=\(\frac{27}{216}\)
\(\color{red}{\textbf{Il y a donc bien plus de chance d'obtenir un 10 que d'obtenir un 9 en 3 lancers de dés.}}\)
\(\color{magenta}{\textbf{Nombre théorique de 9 pour 500 lancers :}}\)
\(\frac{25}{216}\times 500\simeq57 ,87\)
\(\color{magenta}{\textbf{Nombre théorique de 10 pour 500 lancers :}}\)
\(\frac{27}{216}\times 500\simeq62,5\)
\(\color{magenta}{\textbf{Pourcentage théorique de 9 :}}\)
\(\frac{25}{216}\times 100\simeq11,6\%\)
\(\color{magenta}{\textbf{Pourcentage théorique de 10 :}}\)
\(\frac{27}{216}\times 100\simeq12,5\%\)