Principe de la simulation
On va simuler le lancer d'un dé à six faces bien équilibré, c'est-à-dire pour lequel chaque face a autant de chances de « sortir ».
Définition :
Une simulation d'expérience aléatoire consiste à utiliser un générateur pseudo-aléatoire informatique pour simuler la réalisation effective de l'expérience.
Il fournit un nombre pris au hasard dans un intervalle donné.
Complément : I/ Simulation avec un tableur
On combine plusieurs commandes du logiciel.
= ALEA( ) fournit un nombre décimal de l'intervalle [0 ; 1[,
= 6*ALEA( ) fournit un nombre décimal de l'intervalle [0 ; 6[,
= 6*ALEA( )+1 fournit un nombre X décimal de l'intervalle [1 ; 7[.
En prenant la partie entière de « 6*ALEA( )+1 », notée « ENT »,
on obtient alors un nombre entier élément de l'ensemble {1 ; 2 ; 3 ; 4 ; 5 ; 6}.
La formule
= ENT(6*ALEA( )+1) permet donc de simuler le jet d'un dé.
1) En utilisant l'explication précédente, nous allons simuler 1000 tirages d'un dé.
a) Dans la cellule A1, écrire la formule : = ENT(6*ALEA( )+1)
b) Sélectionner la cellule A1, et cliquer dans le champ ![]()
puis y écrire ![]() et valider.
et valider.
c) Choisir le menu "Remplissage\En bas"
ce qui copiera la formule écrite en A1 dans tout le reste de la liste.
d) Appuyer plusieurs sur la touche « F9 » pour faire de nouvelles simulations
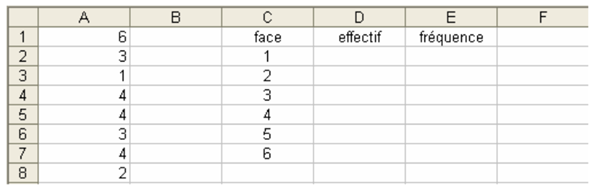
1) Détermination des effectifs :
Pour compter le nombre de 1 qu'il y a dans la colonne A, nous allons utiliser la fonction
NB.SI. Cette fonction compte le nombre de cellules qui répondent à un critère donné
à l'intérieur d'une plage de cellules
Dans la cellule D2, écrire la formule =NB.SI(A$1:A$1000 ;C2) puis étirer la colonne D vers le bas.
2) Détermination des fréquences :
Dans la cellule E2, écrire la formule =D2/1000 et l'étirer vers le bas.
3) Appuyer plusieurs fois sur la touche F9; que constate-t-on au sujet des fréquences ?
Méthode : II/ Simulation d'un dé équilibré sur la calculatrice :

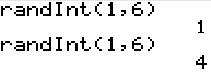
En utilisant la calculatrice, simuler 20 lancers de deux dés équilibrés et compter le nombre de réalisation de chaque événement :
A : “la somme des résultats des deux dés est 9”
B : “la somme des résultats des deux dés est strictement supérieure à 10”
C : “la somme des résultats des deux dés est un multiple de 3”.
Evénement | A | B | C |
|---|---|---|---|
Effectif | |||
Fréquence |
Exemple : Question de compréhension :
On lance un dé équilibré. Que pensez-vous des affirmations suivantes.
a) On obtient 5 une fois sur six.
b) La fréquence du résultat 5 vaut \(\frac{1}{6}\) .
c) La fréquence du résultat 5 s'approche de \(\frac{1}{6}\) au fur et à mesure que le nombre de lancers augmente.
d) La probabilité du résultat 5 vaut \(\frac{1}{6}\).