Exercice : Vidéo Digicode
A écouter :

Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Une porte est munie d'un clavier portant les touches 0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
La porte s'ouvre lorsqu'on frappe dans l'ordre 3 chiffres et 2 lettres qui forment un code.
\(\color{magenta}{\textbf{Les chiffres sont distincts, les lettres peuvent être identiques.}}\)
On suppose dans tout l'exercice que les manipulateurs connaissent le mode d'emploi du dispositif.
1. Quelle est la probabilité pour qu'une personne ouvre la porte au 1er essai si :
Question
a. Elle ignore le code.
Solution
Déterminons Card Ω
Chaque issue est de la forme \(\color{magenta}{(c_1;c_2:c_3;l_1;l_2)}\) avec :
• pour \(c_1\): 10 choix possibles
•pour \(c_2\): 9 choix possibles
•pour \(c_3\): 8 choix possibles
•pour \(l_1\) : 2 choix possibles
•pour \(l_2\) : 2 choix possibles
soit un total de 10× 9 × 8 × 2 × 2 =2880 issues donc \(\color{red}{card Ω = 2880}\).
La probabilité pour qu'une personne ouvre la porte au 1er essai si elle ignore le code est p(A)=\(\frac{1}{2880}\).
Question
b. Elle se souvient seulement que les 3 chiffres du code sont pairs.
Solution
B : « Les 3 chiffres du code sont pairs ».
• pour \(c_1\): 5 choix possibles (0,2,4,6,8)
• pour \(c_2\): 4 choix possibles
• pour \(c_3\): 3 choix possibles
•pour \(l_1\): 2 choix possibles
•pour \(l_2\): 2 choix possibles
soit un total de 240 issues donc \(p(B) =\frac{1}{240}\)
Question
c. Elle se souvient que les deux lettres sont identiques.
Solution
C : « Les deux lettres sont identiques ».
• pour \(c_1\): 10 choix possibles
• pour \(c_2\): 9 choix possibles
•pour \(c_3\): 8 choix possibles
•pour \(l_1\) : 2 choix possibles
•pour \(l_2\) :1 seule lettre possible
soit un total de 1440 issues donc Card C=1440 et par suite p(C) = \(\frac{1}{1440}\)
2. La porte est équipée d'un système d'alarme se déclenchant lorsque aucun des 3 chiffres tapés ne fait partie du code.
Une personne ignorant le code tente sa chance.
Question
a.Quelle est la probabilité pour qu'elle provoque l'alarme au premier essai ?
Solution
Soit D : « la personne déclenche l'alarme »
•pour \(c_1\): 7choix possibles
•pour \(c_2\) : 6 choix possibles
•pour \(c_3\) : 5 choix possibles
•pour \(l_1\) : 2 choix possibles
•pour \(l_2 \): 2 choix possibles
soit un total de 840 issues donc Card D=840 et par suite \(p(D) = \frac{840}{2880}=\frac{7}{24}\)
Question
b. Quelle est la probabilité pour qu'elle ne provoque pas l'alarme au premier essai ?
Solution
La probabilité qu'elle ne déclenche pas l'alarme est donc de p(E)=\(1-\frac{7}{24}=\frac{17}{24}\)
Question
c. Elle effectue 4 essais successifs et indépendants.
Quelle est la probabilité pour qu'elle déclenche l'alarme au moins une fois au cours des 4 essais ? Quel est le nombre d'issues de l'univers ?
Solution
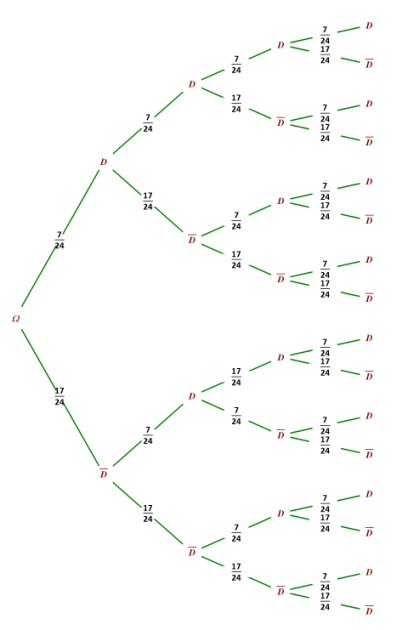
b. F : « elle déclenche l'alarme au moins une fois »
\(\overline{F} : « elle ne déclenche jamais l'alarme ».\)
Les 4 essais sont indépendants et par suite,
on a \(p(\overline{F} )=(p(E))^4\)\(=(\frac{17}{24})^4\)
donc \(p(F)=1–(\frac{17}{24})^4 \simeq 0,748\)
donc 74,8% de chance qu'elle déclenche l'alarme au moins une fois.