Exercice : Problème de Physique
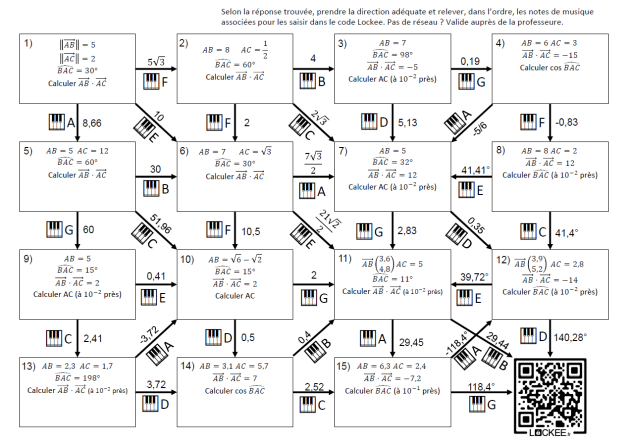
Question
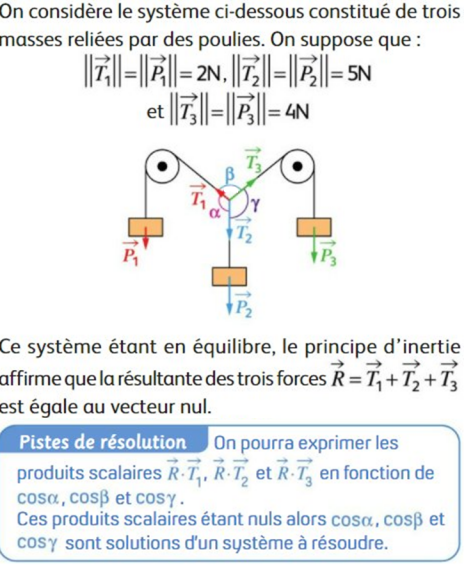
Déterminer les valeurs de \(\alpha,\beta et \gamma\)
Solution
\(\vec{P_1}+\vec{P_2}+\vec{P_3}=\vec{0}\)
or
\(\vec{P_1}=\vec{T_1}\)
\(\vec{P_2}=\vec{T_2}\)
\(\vec{P_3}=\vec{T_3}\)
donc \(\vec{T_1}+\vec{T_2}+\vec{T_3}=\vec{0}\)
\(\vec{T_1}.(\vec{T_1}+\vec{T_2}+\vec{T_3})=\vec{T_1}.\vec{0}=0\)
car le produit scalaire de tout vecteur et du vecteur nul est nul.
\(\iff ||\vec{T_1}|| \times ||\vec{T_1}|| cos((\vec{T_1};\vec{T_1}))+||\vec{T_1}|| \times ||\vec{T_2}|| cos((\vec{T_1};\vec{T_2}))+||\vec{T_1}|| \times ||\vec{T_3}|| cos((\vec{T_1};\vec{T_3}))=0\)
\(\iff 2 \times 2 \times cos(0°)+2 \times 5 \times cos(\alpha)+2 \times 4 \times cos(\beta)=0\)
\(\iff 4+10cos(\alpha)+8cos(\beta)=0\)
\(\vec{T_2}.(\vec{T_1}+\vec{T_2}+\vec{T_3})=\vec{T_2}.\vec{0}=0\)
car le produit scalaire de tout vecteur et du vecteur nul est nul.
\(\iff ||\vec{T_2}|| \times ||\vec{T_1}|| cos((\vec{T_2};\vec{T_1}))+||\vec{T_2}|| \times ||\vec{T_2}|| cos((\vec{T_2};\vec{T_2})+||\vec{T_2}|| \times ||\vec{T_3}|| cos((\vec{T_2};\vec{T_3}))=0\)
\(\iff 5 \times 2 \times cos(\alpha)+5 \times 5 \times cos(0°)+5 \times 4 \times cos(\gamma)=0\)
\(\iff 10 cos(\alpha)+25+20 cos(\gamma)=0\)
\(\vec{T_3}.(\vec{T_1}+\vec{T_2}+\vec{T_3})=\vec{T_3}.\vec{0}=0\)
car le produit scalaire de tout vecteur et du vecteur nul est nul.
\(\iff ||\vec{T_3}|| \times ||\vec{T_1}|| cos((\vec{T_3};\vec{T_1})+||\vec{T_3}|| \times ||\vec{T_2}|| cos((\vec{T_3};\vec{T_2})+||\vec{T_3}|| \times ||\vec{T_3}|| cos(0°)=0\)
\(\iff 4 \times 2 cos(\beta)+4 \times 5 cos(\gamma))+4 \times 4 \times cos(0°)=0\)
\(\iff 8 cos(\beta)+20 cos(\gamma)+16=0\)
En reprenant les 3 équations obtenues :
\(\begin{cases}4+10cos(\alpha)+8cos(\beta)=0\\10 cos(\alpha)+25+20 cos(\gamma)=0\\8 cos(\beta)+20 cos(\gamma)+16=0\end{cases}\)
\(\iff \begin{cases}2+5cos(\alpha)+4cos(\beta)=0\\2 cos(\alpha)+5+4 cos(\gamma)=0\\2 cos(\beta)+5cos(\gamma)+4=0\end{cases}\)
\(\iff \begin{cases}5cos(\alpha)+4cos(\beta)=-2\\2 cos(\alpha)+4 cos(\gamma)=-5\\2 cos(\beta)+5cos(\gamma)=-4\end{cases}\)
\(\iff \begin{cases}5cos(\alpha)+4cos(\beta)+0cos(\gamma)=-2\\2 cos(\alpha)+0cos(\beta)+4 cos(\gamma)=-5\\0cos(\alpha)+2 cos(\beta)+5cos(\gamma)=-4\end{cases}\)
En posant \(\begin{cases}x=cos(\alpha)\\y=cos(\beta)\\z=cos(\gamma) \end{cases}\)
\(\Rightarrow \begin{cases}5x+4y+0z=-2\\2x+0y+4z=-5\\0x+2 y+5z=-4\end{cases}\)


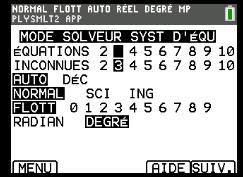

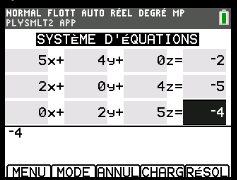

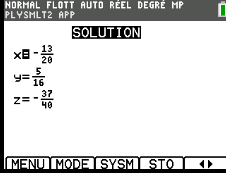
donc \(\begin{cases}x=cos(\alpha)=\frac{-13}{20}\\y=cos(\beta)=\frac{5}{16}\\z=cos(\gamma) =\frac{-37}{40}\end{cases}\)
\(\iff \begin{cases}\alpha=Arccos(\frac{-13}{20})\\\beta=Arccos(\frac{5}{16})\\\gamma =Arccos(\frac{-37}{40})\end{cases}\)
Arrondi au degré :
\(\iff \begin{cases}\alpha=Arccos(\frac{-13}{20})\simeq 131°\\\beta=Arccos(\frac{5}{16})\simeq 72° \\\gamma =Arccos(\frac{-37}{40})\simeq 158°\end{cases}\)
Par le calcul :
\(\begin{cases}5x+4y+0z=-2\\2x+0y+4z=-5\\0x+2 y+5z=-4\end{cases}\)
\(\iff \begin{cases}5x+4y+0z=-2\\0x+2 y+5z=-4\\10x+0y+20z=-25\end{cases}\)
\(\iff \begin{cases}5x+4y+0z=-2\\0x+2 y+5z=-4\\0x-8y+20z=-21 L_3-2L_1\end{cases}\)
\(\iff \begin{cases}5x+4y+0z=-2\\0x+2 y+5z=-4\\0x+0y+40z=-37 L_3+4L_2\end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y+5z=-4\\40z=-37 L_3+4L_2\end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y+5z=-4\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y+5 \times \frac{-37}{40}=-4\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y+ \frac{-37}{8}=-4\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y=-4+\frac{37}{8}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y=-\frac{32}{8}+\frac{37}{8}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\2 y=\frac{5}{8}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4y=-2\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+4 \times \frac{5}{16} =-2\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x+ \frac{5}{4} =-2\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x =-2-\frac{5}{4}\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x =-\frac{8}{4}-\frac{5}{4}\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}5x =-\frac{13}{4}\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)
\(\iff \begin{cases}x =-\frac{13}{20}\\y=\frac{5}{16}\\z=\frac{-37}{40} \end{cases}\)