Exercice : Difficile 4 : Triangle rectangle
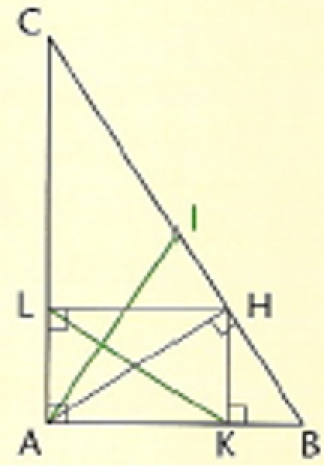
ABC est un triangle rectangle en A, I est le milieu de [BC], H est le pied de la hauteur issue de A,
L et K sont les projetés orthogonaux de H sur (AC) et (AB) respectivement.
Démontrer que (AI) et (LK) sont perpendiculaires
Question
1. Montrer que \(\vec{AI} = \vec{AB} + \frac{1}{2} \vec{BC}\)
Indice
Par la relation de Chasles :
\(\vec{AI} = \vec{AB} + \vec{BI}\)
or I est le milieu de [BC]
donc \(\vec{BI}=\frac{1}{2} \vec{BC}\)
Finalement : \(\vec{AI} = \vec{AB} +\frac{1}{2} \vec{BC}\)
Question
2. En introduisant le point A dans le vecteur \(\vec{BC}\) montrer que
\(\vec{AI} = \frac{1}{2}(\vec{AB} + \vec{AC})\)
Solution
\(\vec{AI} = \vec{AB} +\frac{1}{2} \vec{BC}\)
Par la relation de Chasles :
\(\vec{BC} =\vec{BA} + \vec{AC}\)
\(\vec{AI} = \vec{AB} +\frac{1}{2} (\vec{BA} + \vec{AC})\)
\(\iff \vec{AI} = \vec{AB} +\frac{1}{2} \vec{BA} + \frac{1}{2} \vec{AC}\)
\(\iff \vec{AI} = \vec{AB} -\frac{1}{2} \vec{AB} + \frac{1}{2} \vec{AC}\)
\(\iff \vec{AI} = \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{AC}\)
\(\iff \vec{AI} = \frac{1}{2}( \vec{AB} + \vec{AC})\)
Question
3.Justifier que
\(\vec{AB}\cdot\vec{LK}\)=\(\vec{AB}\cdot\vec{AK}\)=\(\vec{AB}\cdot\vec{AH}\)
Solution
L se projette orthogonalement en A sur (AB) donc :
\(\vec{AB}\cdot\vec{LK}\)=\(\vec{AB}\cdot\vec{AK}\)
H se projette en K sur (AB)
donc :
\(\vec{AB}\cdot\vec{AK}\)=\(\vec{AB}\cdot\vec{AH}\)
Finalement :
\(\vec{AB}\cdot\vec{LK}=\vec{AB}\cdot\vec{AH}\)
Question
4.Justifier que
\(\vec{AC}\cdot\vec{LK}\)=\(\vec{AC}\cdot\vec{LA}=-\vec{AC}\cdot\vec{AH}\)
Solution
K se projette orthogonalement en A sur (AC) donc :
\(\vec{AC}\cdot\vec{LK}\)=\(\vec{AC}\cdot\vec{LA}\)
H se projette en L sur (AB)
donc :
\(\vec{AC}\cdot\vec{LA}\)=\(\vec{AC}\cdot\vec{HA}\)=-\(\vec{AC}\cdot\vec{AH}\)
Finalement :
\(\vec{AC}\cdot\vec{LK}=-\vec{AC}\cdot\vec{AH}\)
Question
5.Montrer que le produit scalaire \(\vec{AI} \cdot \vec{LK}\) est nul.
Solution
\(\vec{AI} \cdot \vec{LK}\) =\(\frac{1}{2}(\vec{AB}+\vec{AC})\cdot\vec{LK}\)
\(=\frac{1}{2}\vec{AB}\cdot\vec{LK}+\frac{1}{2}\vec{AC}\cdot\vec{LK}\)
\(=\frac{1}{2}\vec{AB}\cdot\vec{AK}+\frac{1}{2}\vec{AC}\cdot(\vec{LA})\)
\(=\frac{1}{2}\vec{AB}\cdot\vec{AH}+\frac{1}{2}\vec{AC}\cdot(-\vec{AH})\)
\(=\frac{1}{2}(\vec{AB}-\vec{AC})\cdot(\vec{AH})\)
\(=\frac{1}{2}(\vec{AB}+\vec{CA})\cdot(\vec{AH})\)
\(=\frac{1}{2}(\vec{CB})\cdot(\vec{AH})=0\)
Question
6.Que peut on en déduire pour les droites (BC) et (AH) ?
Solution
(AI) est donc perpendiculaire à (LK)