Exercice : Difficile 6 Carré
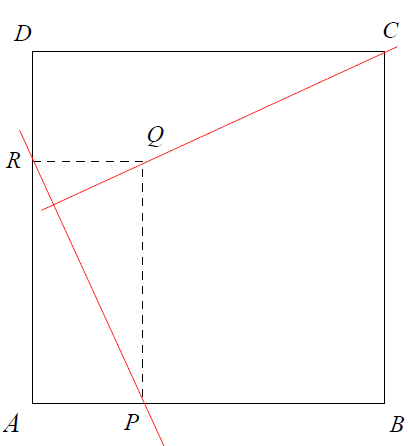
Soit un carré ABCD.
On construit un rectangle APQR tel que :
· P et R sont sur les côtés [AB] et [AD] du carré
· AP = DR
Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.
Question
Justifier que :
\(\vec{QC}. \vec{PR}=\vec{QC}. ( \vec{AR}– \vec{AP})\))
Solution
On utilise la relation de Chasles :
\(\vec{QC}. \vec{PR}=\vec{QC}. ( \vec{PA} + \vec{AR}\))
\(\iff \vec{QC}. \vec{PR}=\vec{QC}. ( -\vec{AP} + \vec{AR}\))
\(\iff \vec{QC}. \vec{PR}=\vec{QC}. ( \vec{AR}-\vec{AP}\))
Question
2.
On appelle \(a\) la longueur du côté du carré et \(l\) la longueur AP
Exprimer les vecteurs \(\vec{AR}\) ,\(\vec{AP}\) et \(\vec{QC}\) dans la base \((A ; \vec{AB} ;\vec{AC})\)
Solution
\(\vec{AR}=(a-l)\vec{AD}\)
\(\vec{AP}=l\vec{AB}\)
\(\vec{QC}=(a-l)\vec{AB}+l\vec{AD}\)
Question
2.En déduire que les droites (QC) et (PR) sont perpendiculaires.
Solution
\(\vec{QC}. \vec{PR}=\vec{QC}. ( \vec{AR}-\vec{AP}\))
\(\iff \vec{QC}. \vec{PR}=((a-l)\vec{AB}+l\vec{AD}). ((a-l)\vec{AD}-l\vec{AB}\))
\(\iff \vec{QC}. \vec{PR}=(a-l)\vec{AB}.(a-l)\vec{AD}+(a-l)\vec{AB}(-l\vec{AB})+l\vec{AD}. (a-l)\vec{AD}+l\vec{AD}.(-l\vec{AB})\))
\(\iff \vec{QC}. \vec{PR}=(a-l)^2\vec{AB}.\vec{AD}-l(a-l)\vec{AB}.\vec{AB}+l(a-l)\vec{AD}.\vec{AD}-l^2\vec{AD}.\vec{AB}\)
\(\vec{AB}.\vec{AD}=\vec{AD}.\vec{AB}=0\) car les vecteurs \(\vec{AB}\) et \(\vec{AD}\) sont orthogonaux,[AB] et [AD] sont deux côtés consécutifs d'un carré.
\(\iff \vec{QC}. \vec{PR}=-l(a-l)\vec{AB}.\vec{AB}+l(a-l)\vec{AD}.\vec{AD}\)
\(\vec{u}.\vec{u}=||\vec{u}||.||\vec{u}||.cos((\vec{u} ;\vec{u}))=||\vec{u}||^2.cos(0)=||\vec{u}||^2\)
\(\iff \vec{QC}. \vec{PR}=-l(a-l)AB^2+l(a-l)AD^2\)
Or AB=AC car
\(\iff \vec{QC}. \vec{PR}=-l(a-l)AB^2+l(a-l)AD^2\)
[AB] et [AD] sont deux côtés consécutifs d'un carré.
donc \(AB^2=AC^2\)
\(\iff \vec{QC}. \vec{PR}=l(a-l)(AD^2-AB^2)\)
\(\iff \vec{QC}. \vec{PR}=l(a-l) \times 0\)
donc les vecteurs \(\vec{QC}\) et \(\vec{PR}\) sont orthogonaux
et les droites \((QC)\) et \((PR)\) sont perpendiculaires.