Exercice : Difficile 5 : Drapeau
Question
Un grand drapeau de la forme d'un triangle équilatéral est suspendu
par deux de ses coins au sommet de mats verticaux de 3 et 4 mètres
de haut. Le troisième coin affleure exactement au sol.
Quelles sont les dimensions exactes de ce drapeau ?
Indice
L'observation de la figure doit vous faire penser aux triangles rectangles,
donc au théorème de Pythagore et aux formules de trigonométrie.
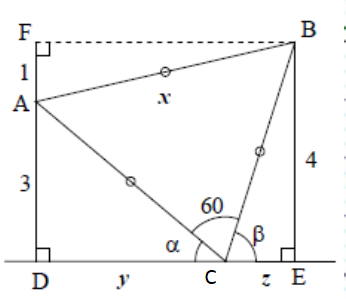
On pose AB = BC = CA = \(x\), DC = \(y\) et CE = \(z\).
Les triangles ADC, BCE et AFE sont rectangles respectivement
en D, E et F, donc d'après la propriété de Pythagore, on a :
\(AC^2 = AD^2 + DC^2\) soit \(x^2 = 9 + y^2\) soit \(y^2 = x^2 - 9\) (1)
\(BC^2 = BE^2 + EC^2\) soit \(x^2 = 16 + z^2\) soit \(z^2 = x^2 - 16\) (2)
\(AB^2 = AF^2 + FB^2\) soit \(x^2 = 1 + (y + z)^2\)
soit \(x^2 = 1 + y^2 + z^2 + 2yz\) (3)
L'addition de (1) et (2) nous donne :
\(y^2 + z^2 = 2x^2 - 25\)
On remplace dans (3) :\( x^2 = 1 + (2x^2 - 25) + 2yz\) donc
\(2yz = x^2 -1 - 2x^2 + 25\) soit
\(2yz = 24 - x^2\)
soit \(4y^2z^2 = (24 - x^2)^2\)
On remplace \(y^2\) et \(z^2\) par leur valeur donnée en (1) et (2) :
\(4(x^2 -9)(x^2 - 16) = (24 - x^2)^2\)
On obtient donc :
\(4(x^4 - 16x^2 - 9x^2 + 144) = 576 - 48x^2 + x^4\)
\(\leftrightarrow\) \(4x^4 -100x^2 + 576 = 576 - 48x^2 + x^4\)
\(\leftrightarrow\)\( 3x^4 + 52x^2 = 0\)
\(\leftrightarrow\)\( x^2(3x^2 + 52) = 0\)
\(\leftrightarrow\) \(x^2 = 0\) ou \(3x^2 + 52 = 0\)
\(\leftrightarrow\) x = 0 ou x = \(\sqrt{\frac{52}{3}}\) ou \(x = -\sqrt{\frac{52}{3}}\)
Or \(x\) est une longueur non nul, donc le côté du drapeau mesure \(\sqrt{\frac{52}{3}}\) mètres, soit environ environ 4,16 mètres.
Question
Autre méthode avec la trigonométrie.
Solution

On sait que DCE est un angle plat, donc \(\alpha + 60 + \beta = 180\)
, donc \(\alpha + \beta = 120\)
soit \(\beta = 120-\alpha.\)
Donc
\(sin \beta= sin(120 -\alpha) = sin120 cos \alpha - cos120 sin \alpha =\frac{\sqrt{3}}{2}cos \alpha -\frac{-1}{2}sin \alpha\)
Donc
\(sin \beta= \frac{\sqrt{3}}{2}cos \alpha +\frac{1}{2}sin \alpha\) (Eq)
Dans le triangle ABD rectangle en D, on a :
\(cos \alpha = \frac{y}{x}\)
et
\(sin \alpha = \frac{3}{x}\)
Dans le triangle BEC rectangle en E, on a : \(sin \beta= \frac{4}{x}\)
On remplace \(cos \alpha\), \(sin \alpha\) et \(sin \beta\) par leur valeur dans (Eq) :
\(\frac{4}{x}= \frac{\sqrt{3}}{2}\frac{y}{x} +\frac{1}{2}\frac{3}{x}\)
On obtient alors :
\(2 \times 4 = \sqrt{3} y + 3 soit y = \frac{8-3}{\sqrt{3}}\)
soit \(y = \frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{3}\)
Or le triangle ADC est rectangle en D,
donc d'après la propriété de Pythagore, on a :
\(AC^2 = AD^2 + DC^2\)
soit \(x^2 = 9 + y^2\)
soit \(x^2 = 9 + \frac{25}{3} = \frac{52}{3}\)
soit \(x = \sqrt{\frac{52}{3}}\) ou \(x = -\sqrt{\frac{52}{3}}\)
Comme \(x\) est une longueur, on obtient : \(x = \sqrt{\frac{52}{3}}\)