Exercice : Difficile 1 : Triangle rectangle

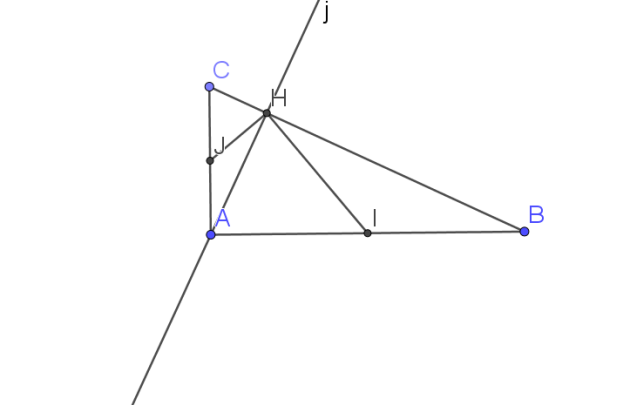
Soit ABC un triangle rectangle en A.

I et J sont les milieux respectifs des côtés [AB] et [AC]

H est le le pied de la hauteur issue de A.

Difficile.ggb [ggb, 9,4 ko]

1.Démontrer les égalités suivantes :

Question

a. \(\vec{AB}\cdot\vec{HC}=\vec{HB}\cdot\vec{HC}\)

Solution

Le projeté orthogonal de A sur la droite (HC) est le point H.

donc le projeté orthogonal du vecteur \(\vec{AB}\) est \(\vec{HB}\)

finalement :

\(\vec{AB}\cdot\vec{HC}=\vec{HB}\cdot\vec{HC}\)

Question

b.\(\vec{AB}\cdot\vec{HA}=\vec{AB}\cdot\vec{HC}\)

Indice

Introduire le point C par la relation de Chasles dans le vecteur \(\vec{HA}\)

Solution

\(\vec{AB}\cdot\vec{HA}=\vec{AB}\cdot(\vec{HC}+\vec{CA})\)

\(\iff \vec{AB}\cdot\vec{HA}=\vec{AB}\cdot \vec{HC}+\vec{AB}\cdot \vec{CA}\)

or \(\vec{AB}\cdot \vec{CA}=0\) car les vecteurs \(\vec{AB}\) et \(\vec{CA}=-\vec{AC}\) sont orthogonaux.

\(\iff \vec{AB}\cdot\vec{HA}=\vec{AB}\cdot \vec{HC}\)

Question

c.\(\vec{HA}+\vec{HB}=2\vec{HI}\)

Indice

Introduire le point I par la relation de Chasles dans les vecteurs \(\vec{HA}\) et \(\vec{HB}\)

Solution

\(\vec{HA}+\vec{HB}\)

=\(\vec{HI}+\vec{IA}+\vec{HI}+\vec{IB}\)

I milieu de [AB] donc \(\vec{IA}=-\vec{IB}\)

Finalement

\(\vec{HA}+\vec{HB}\)

=\(2\vec{HI}\)

Question

d.\(\vec{HA}+\vec{HC}=2\vec{HJ}\)

Indice

Introduire le point J par la relation de Chasles dans les vecteurs \(\vec{HA}\) et \(\vec{HB}\)

Solution

\(\vec{HA}+\vec{HC}\)

\(=\vec{HJ}+\vec{JA}+\vec{HJ}+\vec{JC}\)

or J milieu de [AC] donc \(\vec{JA}=-\vec{JC}\)

Finalement :

\vec{HA}+\vec{HC}=2\vec{HJ}

Question

2. En déduire que \(\vec{HB}\cdot\vec{HC}=-AH^2\)

Indice

Montrer que \(\vec{HB}\cdot\vec{HC}=\vec{AB}\cdot\vec{HA}\) grâce aux questions 1. a. et 1. b. puis projeter \(\vec{AB}\) sur \(\vec{HA}\)

Solution

\(\vec{HB}\cdot\vec{HC}=\vec{AB}\cdot\vec{HC}(1.a.)=\vec{AB}\cdot\vec{HA}(1.b.)\)

Le projeté de A sur (AH) est A

Le projeté de B sur (AH) est H

donc

\(\iff \vec{HB}\cdot\vec{HC}=\vec{AH}\cdot\vec{HA}=\vec{AH}\cdot(-\vec{AH})\)

\(\iff \vec{HB}\cdot\vec{HC}=-AH^2\)

Question

3.En déduire que \(\vec{HI}\cdot\vec{HJ}=0\)

Solution

\(\vec{HI}\cdot\vec{HJ}=\frac{1}{2}(\vec{HA}+\vec{HB})\cdot\frac{1}{2}(\vec{HA}+\vec{HC})\)

\(\iff \vec{HI}\cdot\vec{HJ}=\frac{1}{4}(\vec{HA}+\vec{HB})\cdot(\vec{HA}+\vec{HC})\)

\(\iff \vec{HI}\cdot\vec{HJ}=\frac{1}{4}(\vec{HA}\cdot\vec{HA}+\vec{HA}\cdot\vec{HC}+\vec{HB}\cdot\vec{HA}+\vec{HB}\cdot\vec{HC})\)

\(\iff \vec{HI}\cdot\vec{HJ}=\frac{1}{4}(HA^2+\vec{HA}\cdot\vec{HC}+\vec{HB}\cdot\vec{HA}+\vec{HB}\cdot\vec{HC})\)

\(\vec{HA}\cdot\vec{HC}=0\)

car les vecteurs \(\vec{HA}\) et \(\vec{HC}\) sont orthogonaux.

\(\vec{HB}\cdot\vec{HA}=0\)

car les vecteurs \(\vec{HA}\) et \(\vec{HB}\) sont orthogonaux.

\(\iff \vec{HI}\cdot\vec{HJ}=\frac{1}{4}(HA^2-AH^2)=0\)

Question

5.Que pouvez vous conclure ?

Solution

On en déduit que les droites (HI) et (HJ) sont orthogonaux.