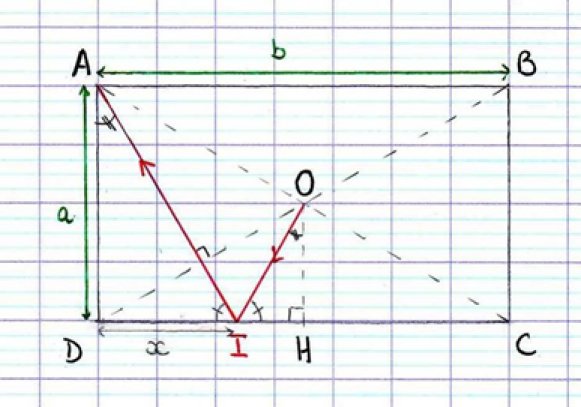
Exercice : Difficile 3 : Billard
On considère un billard américain rectangulaire ABCD, tel que AD=\(a\) et AB=\(b\).
Une boule placée au centre O du billard rentre dans le trou placé en A, après un seul rebond sur la bande (CD).
On s'aperçoit alors que (IA) est orthogonale à la droite (BD).
Quel est le format du rectangle ?
Question
1.Justifier que \(\vec{AI} .\vec{DB}=0\)
Solution
\(\vec{AI} .\vec{DB}=0\) car les droites (AI) et (DB) sont perpendiculaires
donc les vecteurs \(\vec{AI}\) et \(\vec{DB}\) sont orthogonaux.
Question
2. Dans le repère (D ;\(\vec{DC}\);\(\vec{DA}\))
donner les coordonnées des vecteurs \(\vec{AI}\) et \(\vec{DB}\)
Solution
Dans le repère (D ;\(\vec{DC}\);\(\vec{DA}\)) ,
les coordonnées du vecteur\(\vec{AI}\) sont \(\begin{array}[c]x\\-a\end{array}\)
celles du vecteur \(\vec{DB}\) sont \(\begin{array}[c]b\\a\end{array}\)
Question
3. En déduire que \(x\times b-a^2 =0\) (Equation 1)
Solution
\(\vec{AI}\) . \(\vec{DB}\)=0
\(\iff \begin{array}[c]x\\-a\end{array}. \begin{array}[c]b\\a\end{array}=0\)
\(\iff xb-a^2=0\)
Question
4.
Soit O' le symétrique de O par rapport à la droite (DC)
En utilisant le théorème de Thalès dans les triangles ADI et O'HI montrer que
\(\frac{a}{\frac{a}{2}}=\frac{x}{\frac{b}{2}-x}\)
Solution
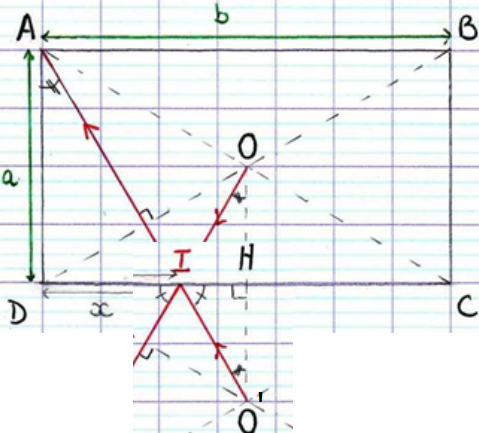
Les points O'IA et HID sont alignés dans le même ordre.
Les droites (AD) et (OH) sont parallèles.
\(\frac{O'H}{AD}=\frac{HI}{ID}=\frac{O'I}{IA}\)
\(\iff \frac{\frac{a}{2}}{a}=\frac{\frac{b}{2}-x}{x}=\frac{O'I}{IA}\)
donc
\(\frac{\frac{a}{2}}{a}=\frac{\frac{b}{2}-x}{x}\)
En inversant les deux fractions :
\(\frac{a}{\frac{a}{2}}=\frac{x}{\frac{b}{2}-x}\)
Question
5.En déduire que \(x=\frac{b}{3}\)
Solution
\(\frac{a}{\frac{a}{2}}=\frac{x}{\frac{b}{2}-x}\)
On calcule le produit en croix :
\(a(\frac{b}{2}-x)=\frac{a}{2}\times x\)
On simplifie par a :
\(\frac{b}{2}-x=\frac{1}{2}\times x\)
\(\iff -x=\frac{1}{2}\times x-\frac{b}{2}\)
\(\iff -x-\frac{1}{2}\times x=-\frac{b}{2}\)
\(\iff -\frac{3}{2}\times x=-\frac{b}{2}\)
\(\iff \frac{3}{2}\times x=\frac{b}{2}\)
\(\iff x=\frac{\frac{b}{2}}{\frac{3}{2}}\)
\(\iff x=\frac{b}{2} \times \frac{2}{3}\)
\(\iff x=\frac{b}{3}\)
Question
6.En remplaçant dans l' Equation 1, montrer que \(b=\sqrt{3}a\)
Solution
\(x\times b-a^2 =0\)
\(\iff \frac{b}{3}\times b-a^2 =0\)
\(\iff \frac{b^2}{3}-a^2 =0\)
\(\iff -a^2 =-\frac{b^2}{3}\)
\(\iff a^2 =\frac{b^2}{3}\)
\(\iff 3a^2 =b^2\)
\(\iff b=\sqrt{3}a\) ou \(b=-\sqrt{3}a\)
or \(b\) est une longueur
donc \(b=\sqrt{3}a\)
Question
7.Conclure
Solution
Les dimensions du rectangle sont \(a\) et \(\sqrt{3}a\)