Exercice : Difficile 7 Triangle
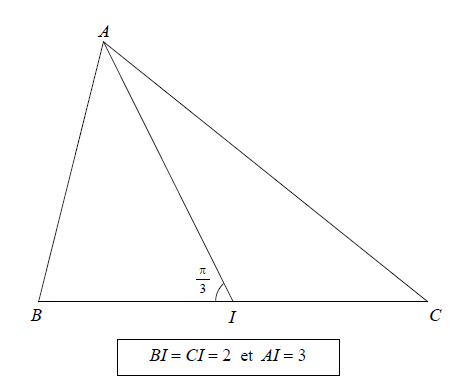
ABC est un triangle et I est le milieu de [BC].
(Voir les données sous la figure)
Calculer :
Question
\(\vec{AB}. \vec{AC}\)
Solution
\(\vec{AB}. \vec{AC}\)
=\((\vec{AI}+\vec{IB}). (\vec{AI}+\vec{IC})\)
=\(\vec{AI}.\vec{AI} + \vec{AI}.\vec{IC}+\vec{IB}. \vec{AI}+\vec{IB}. \vec{IC})\)
=\(AI^2 + \vec{AI}.(\vec{IC}+\vec{IB})+\vec{IB}. \vec{IC})\)
or \(\vec{IC}=-\vec{IB}\)
=\(AI^2 + \vec{AI} \times 0+\vec{IB}. (-\vec{IB})\)
=\(3^2 - \vec{IB} . \vec{IB})\)
=\(3^2 - IB^2\)
=\(3^2 - 2^2\)
=\(9 -4\)
=\(5\)
Question
2.\(AB^2 + AC^2\)
Solution
\(\vec{AB}. \vec{AC}=\frac{1}{2}(AB^2+AC^2-(\vec{AB}-\vec{AC})^2)\)
\(\iff \vec{AB}. \vec{AC}=\frac{1}{2}(AB^2+AC^2-(\vec{AB}+\vec{CA})^2)\)
\(\iff \vec{AB}. \vec{AC}=\frac{1}{2}(AB^2+AC^2-(\vec{CB})^2)\)
\(\iff \vec{AB}. \vec{AC}=\frac{1}{2}(AB^2+AC^2-CB^2)\)
\(\iff 5=\frac{1}{2}(AB^2+AC^2-4^2)\)
\(\iff 10=AB^2+AC^2-16\)
\(\iff 10+16=AB^2+AC^2\)
\(\iff AB^2+AC^2=26\)
Question
3.\(AB^2 – AC^2\)
Solution
\(AB^2 – AC^2=(\vec{AB})^2-(\vec{AC})^2\)
\(\iff AB^2 – AC^2=(\vec{AB}+\vec{AC})(\vec{AB}-\vec{AC})\)
\(\iff AB^2 – AC^2=(\vec{AB}+\vec{AC})(\vec{AB}+\vec{CA})\)
\(\iff AB^2 – AC^2=(\vec{AB}+\vec{AC})(\vec{CB})\)
\(\vec{AB}+\vec{AC}=\vec{AI}+\vec{IB}+\vec{AI}+\vec{IC}=2\vec{AI}\)
car \(\vec{IB}=-\vec{IC}\)
\(\iff AB^2 – AC^2=2\vec{AI} . \vec{CB}=2||\vec{AI}|| \times ||\vec{CB}|| \times cos((\vec{AI};\vec{CB}))\)
\(\iff AB^2 – AC^2=2 \times AI \times CB \times cos((\vec{AI};\vec{CB}))\)
\(\iff AB^2 – AC^2=2 \times 3 \times 4 \times cos(-(\pi - \frac{\pi}{3}))\)
\(\iff AB^2 – AC^2=2 \times 3 \times 4 \times cos(-\frac{2\pi}{3})\)
\(\iff AB^2 – AC^2=2 \times 3 \times 4 \times cos(\frac{2\pi}{3})\)
\(\iff AB^2 – AC^2=2 \times 3 \times 4 \times \frac{-1}{2}\)
\(\iff AB^2 – AC^2=-12\)
Question
4.AB et AC
Solution
\(AB^2+AC^2=26\) (L1)
\(AB^2 – AC^2=-12\) (L2)
donc
\(2AB^2=14\) (L1+L2)
\(\iff AB^2=7\)
\(\iff AB=\sqrt{7}\)
\(2AC^2=38\) (L1-L2)
\(AC^2=19\)
\(AC=\sqrt{19}\)