Exercice : Difficile 2 : Trapèze
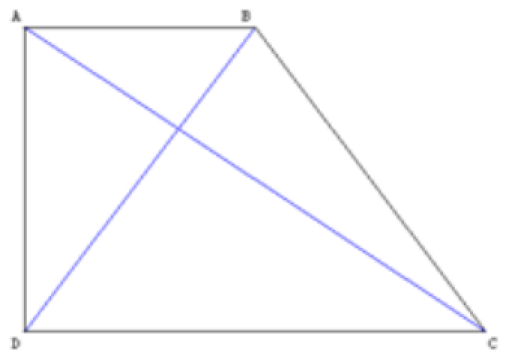
ABCD est un trapèze rectangle en A et D tel que la petite base
AB = \(a\), la grande base DC =\( 2a\) et la hauteur AD = \(h\).
Question
Trouver en fonction de \(a\) la valeur \(h\) pour laquelle les diagonales [AC] et [BD] sont orthogonales.
Indice
1. Les diagonales [AC] et [BD] sont orthogonales si et seulement si \(\vec{AC}\cdot\vec{BD}=0\)
2.Introduire le point A dans le vecteur \(\vec{BD}\) de la relation précédente par la relation de Chasles et le point D dans le vecteur \(\vec{AC}\)
3.En déduire que \(-2a^2 +h^2 =0\)
4. En déduire que \(h=\sqrt{2}a\)
Solution
\(\vec{AC}\cdot\vec{BD}=0\)
\(\iff (\vec{AD}+\vec{DC})\cdot(\vec{BA}+\vec{AD})=0\)
\(\iff \vec{AD}\cdot\vec{BA}+\vec{AD}\cdot\vec{AD}+\vec{DC}\cdot\vec{BA}+\vec{DC}\cdot\vec{AD}=0\)
\(\vec{AD}\cdot\vec{BA}\)=0 car les vecteurs \(\vec{AD}\) et \(\vec{BA}\) sont orthogonaux.
\(\vec{DC}\cdot\vec{AD}\)=0 car les vecteurs \(\vec{DC}\) et \(\vec{AD}\) sont orthogonaux.
\(\iff \vec{AD}^2-DC \times BA=0\)
\(\iff AD^2-DC \times BA=0\)
\(\iff h^2-2a \times a=0\)
\(\iff -2a^2+h^2=0\)
\(\iff h^2=2a^2\)
\(\iff h=\sqrt{2}a\)