QCM3
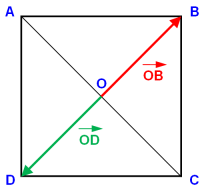
Si ABCD est un carré de centre O tel que AB = 1 alors \(\overrightarrow{OB} . \overrightarrow{OD} = -\frac{1}{2}\).
Votre choixChoix attenduRéponse
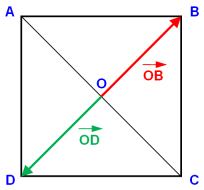
Ici :
- l'angle entre \(\overrightarrow{OB}\) et \(\overrightarrow{OD}\) vaut 180°,
- \(|\overrightarrow{OB}| = |\overrightarrow{OD}| = \frac{DB}{2} = \frac{\sqrt{2}}{2}\).
Donc :
\(\overrightarrow{OB} . \overrightarrow{OD} = ||\overrightarrow{OB}|| \times ||\overrightarrow{OD}|| \times \cos(\overrightarrow{OB}, \overrightarrow{OD}) = \frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2} \times (-1) = -\frac{1}{2}\).