Exercice : Salle de Classe
A l'entrée d'une salle de classe se trouvent 4 interrupteurs identiques un pour chacune des 4 lampes de la classe.
A votre arrivée, vous constatez que le tableau est encore éclairé, et qu'une des trois autres lampes est allumé également.

1. Vous actionnez au hasard l'un des interrupteurs
Calculez la probabilité qu'après cela :
Question
a. Le tableau soit encore éclairé
Solution
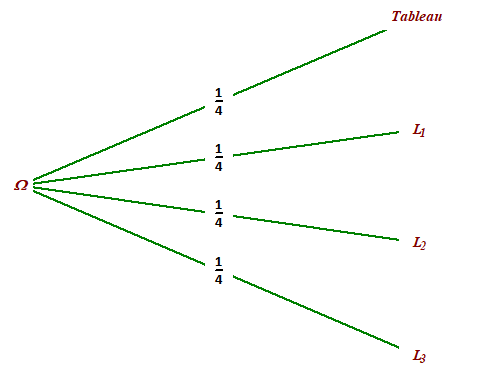
\(p("Le tableau soit encore éclairé")=\frac{3}{4}\)
Il faut actionner n'importe quel interrupteur sauf celui du Tableau.
Question
b. Il y ait trois lampes allumées dans la salle.
Solution
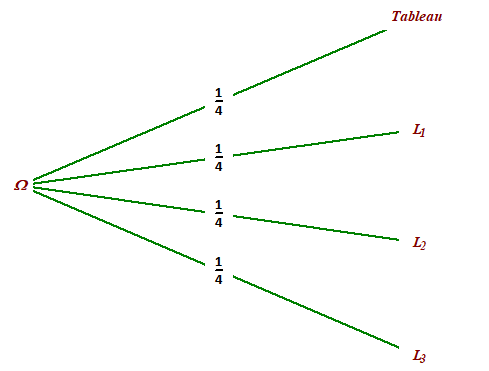
\(p("Trois lampes sont allumées dans la salle de classe")=\frac{2}{4}=\frac{1}{2}\)
Il ne faut pas actionner l'interrupteur d'une lampe déjà allumée.
2. Vous actionnez cette fois successivement deux interrupteurs différents.
Calculez la probabilité qu'après cela :
Question
a. Le tableau ne soit plus éclairé
Solution
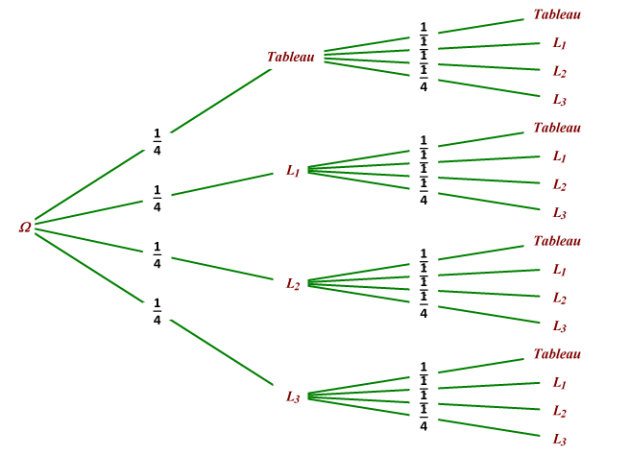
p("Le tableau ne soit plus éclairé")
=p((Tableau,\(L_1\)))+p((Tableau,\(L_2\)))+p((Tableau,\(L_3\)))
+p((\(L_1\),Tableau))+p((\(L_2\),Tableau))+p((\(L_3\),Tableau))
\(=\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}\)
+\(\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}\)
\(=6 \times \frac{1}{4}\times \frac{1}{4}=\frac{6}{16}=\frac{3}{8}\)
Question
b. l'une au moins des deux lampes allumées à votre arrivé le soit encore,
Solution

p("L'une au moins des deux lampes allumées à votre arrivé le soit encore")
\(=p(\overline{"Les deux lampes allumées à votre arrivé sont éteintes"})\)
\(=1-p("Les deux lampes allumées à votre arrivé sont éteintes")\)
Si on suppose que la lampe \(L_1\) soit allumée à l'entrée dans la salle :
\(p("Les deux lampes allumées à votre arrivé sont éteintes")\)
\(=p((L_1,Tableau))+p((Tableau,L_1))\)
\(=\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}\)
\(=\frac{1}{16}+\frac{1}{16}=\frac{2}{16}=\frac{1}{8}\)
p("L'une au moins des deux lampes allumées à votre arrivé le soit encore")
\(=1-\frac{1}{8}=\frac{7}{8}\)
Question
c. les quatre lampes soient allumées
Solution

Si on suppose que la lampe \(L_1\) soit allumée à l'entrée dans la salle :
p("Les quatre lampes soient allumées")
\(=p((L_2,L_3))+p((L_3,L_2))\)
\(=\frac{1}{4}\times \frac{1}{4}+\frac{1}{4}\times \frac{1}{4}\)
\(=\frac{1}{16}+\frac{1}{16}=\frac{2}{16}=\frac{1}{8}\)