Exercice : Star Burst
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
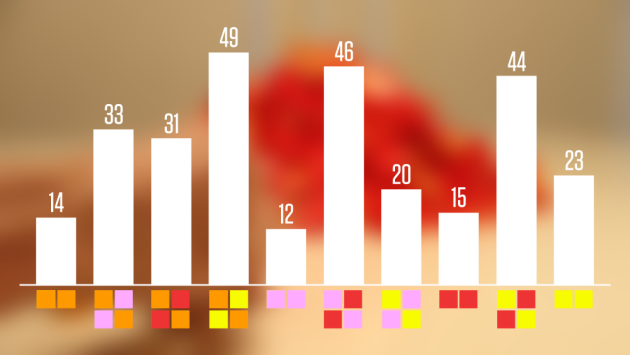
Les couleurs des bonbons disponibles sont :
Question
Sachet que :
un paquet contient deux bonbons
les couleurs sont toutes possibles pour chacun des deux bonbons.
deux bonbons peuvent avoir la même couleur dans un paquet.
Donnez la fréquence d'obtention de chacune des compositions des paquets que je n'aime pas.
Indice
Réaliser un arbre de probabilités.
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
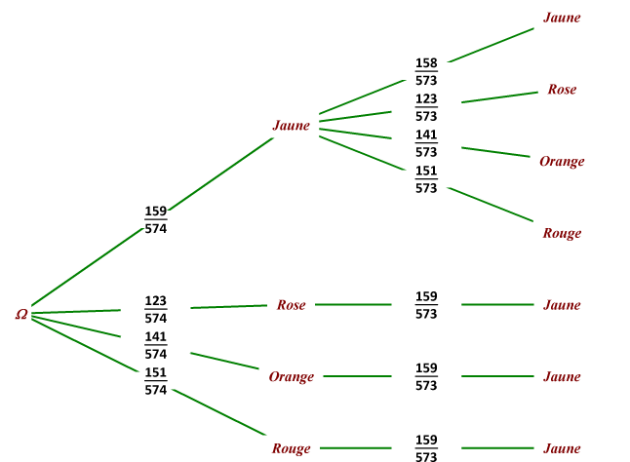
Exemple : Nombre de Bonbons Jaune-Rouge ou Rouge-Jaune:
\((\frac{159}{574}\times \frac{151}{573}+\frac{151}{574} \times \frac{159}{573}) \times 287\)
\(=2(\frac{24 009}{328 902}) \times 287\)
\(=\frac{24 009}{164 451} \times 287\)
\(=\frac{8003}{54 817} \times 287\simeq 42\)
Il devrait y avoir 42 Bonbons Jaune-Rouge ou Rouge-Jaune dans le paquet
Ici, il y en \(44\)
Nombre de Bonbons Jaune-Rose ou Rose-Jaune:
\((\frac{159}{574}\times \frac{123}{573}+\frac{123}{574} \times \frac{159}{573}) \times 287\)
\(=2(\frac{19 557}{328 902}) \times 287\)
\(=\frac{39 114}{328 902} \times 287\)
\(=\frac{6519}{54 817} \times 287\simeq 34\)
Il devrait y avoir 34 Bonbons Jaune-Rose ou Rose-Jaune dans le paquet
Ici, il y en \(20\)
Nombre de Bonbons Jaune-Orange ou Orange-Jaune:
\((\frac{159}{574}\times \frac{141}{573}+\frac{141}{574} \times \frac{159}{573}) \times 287\)
\(=2(\frac{22 419}{328 902}) \times 287\)
\(=\frac{44 838}{328 902} \times 287\)
\(=\frac{7 473}{54 817} \times 287\simeq 39\)
Il devrait y avoir 39 Jaune-Orange ou Orange-Jaune dans le paquet
Nombre de Bonbons Jaune-Jaune:
\(\frac{159}{574}\times \frac{158}{573} \times 287\)
\(=\frac{25 122}{328 902} \times 287\simeq 22\)
Il devrait y avoir 22 Bonbons Jaune-Rouge ou Rouge-Jaune dans le paquet
Ici, il y en \(23\)
Ici, il y en \(49\)
Calcul de la probabilité d'obtenir au moins un bonbon jaune dans le paquet :
\(p(« obtenir au moins un bonbon jaune »)=\frac{159}{574}(\frac{158}{573}+\frac{123}{573}+\frac{141}{573}+\frac{151}{573})+(\frac{123}{574}+ \frac{141}{574}+\frac{151}{574})\times \frac{159}{573}\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{159}{574} \times \frac{573}{573}+\frac{415}{574} \times \frac{159}{573}\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{159}{574} \times 1+\frac{415}{574} \times \frac{159}{573}\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{159}{574}(1+\frac{415}{573})\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{159}{574}(\frac{573}{573}+\frac{415}{573})\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{159}{574} \times \frac{988}{573}\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{157 092}{328 902}\)
\(\iff p(« obtenir au moins un bonbon jaune »)=\frac{26 182}{54 817}\simeq 0,48\)
La probabilité de ne pas avoir un bonbon jaune dans le paquet est donc envrion de \(1-0,48\simeq 0,52\)