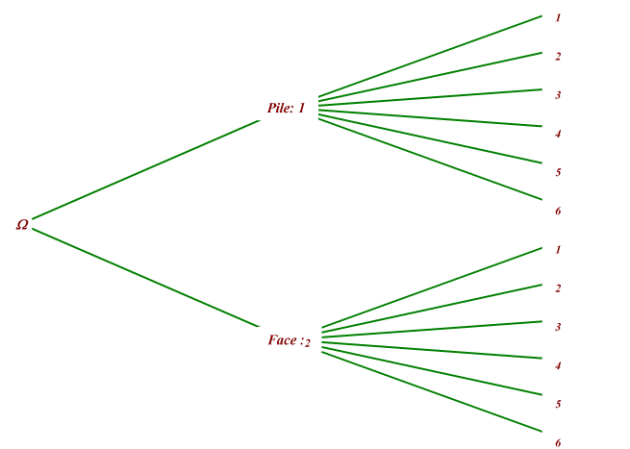
Exercice : Pièce et Dé
Un jeu consiste à lancer simultanément un dé parfait et une pièce équilibrée de 1€.
A pile on associe le nombre 1 et à face le nombre 2.
Un résultat est la somme du numéro obtenu sur le dé et du nombre obtenu par la pièce.


Question
1.Dresser un arbre de toutes les possibilités.
Question
2. En déduire la loi de probabilité des résultats.
Solution
\(s_i\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
p(\(S=s_i\)) | \(\frac{1}{12}\) | \(\frac{2}{12}\) | \(\frac{2}{12}\) | \(\frac{2}{12}\) | \(\frac{2}{12}\) | \(\frac{2}{12}\) | \(\frac{1}{12}\) |
Question
3. Déterminer l'espérance de cette loi de probabilité
Comment interpréter cette grandeur.
Solution
\(E(S)=\frac{1}{12} \times 2+\frac{2}{12} \times 3+\frac{2}{12} \times 4+\frac{2}{12} \times 5+\frac{2}{12} \times 6+\frac{2}{12} \times 7+\frac{1}{12} \times 8\)
\(\iff E(S)=\frac{2}{12}+\frac{6}{12}+\frac{8}{12}+\frac{10}{12}+\frac{12}{12}+\frac{14}{12}+\frac{8}{12}\)
\(\iff E(S)=\frac{60}{12}=5\)
Sur un grand nombre d'expérience, le résultat qu'on a le plus de chance d'obtenir est le 5
4. Déterminer les probabilités suivantes :
Question
a. la somme est impaire ;
Solution
\(p(« la somme est impaire »)=p('2' \cup '4' \cup '6' \cup '8')=\frac{1}{12}+\frac{2}{12}+\frac{2}{12}+\frac{1}{12}=\frac{6}{12}=0,5\)
Question
b. la somme est multiple de 3 ;
Solution
\(p(« la somme est un multiple de 3 »)=p('3' \cup '6' )=\frac{2}{12}+\frac{2}{12}=\frac{4}{12}=\frac{1}{3}\)
Question
c. la somme n'est ni 6, ni 5 ;
Solution
\(p(« la somme n'est ni 6, ni 5 »)=1-p(« la somme est 5 ou 6 » )=1-(\frac{2}{12}+\frac{2}{12})=1-\frac{4}{12}=1-\frac{1}{3}=\frac{2}{3}\)
Question
d. la somme est au moins 4 ;
Solution
\(p("la somme est au moins 4")=p('4' \cup '5' \cup '6' \cup '7' \cup '8')=\frac{2}{12}+\frac{2}{12}+\frac{2}{12}+\frac{2}{12}+\frac{1}{12}=\frac{9}{12}=\frac{3}{4}\)
Question
e. la somme est au plus 3.
Solution
\(p("la somme est au plus 3")=p(\overline{"la somme est au moins 4"})=1-p("la somme est au moins 4"}=1-\frac{3}{4}=\frac{1}{4}\)