Tableau 2
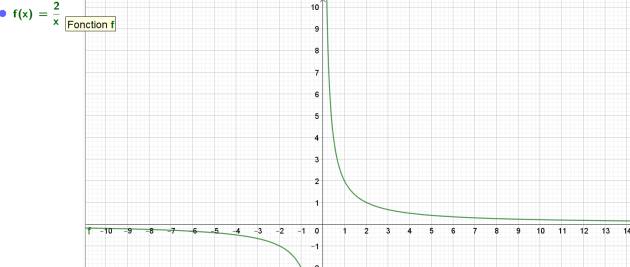
On considère la fonction \(f\) définie par \(f(x) =\frac{2}{x}\) .
Question
1) Compléter le tableau de valeurs puis tracer la représentation graphique de f sur l'intervalle [0,1 ; 5].
\(x\) | 0,1 | 0,2 | 0,5 | 1 | 2 | 4 | 5 |
|---|---|---|---|---|---|---|---|
\(f(x)\) |
Solution
\(x\) | 0,1 | 0,2 | 0,5 | 1 | 2 | 4 | 5 |
|---|---|---|---|---|---|---|---|
\(f(x)\) | \(\frac{2}{0,1}=\frac{2}{\frac{1}{10}}=2 \times 10=20\) | \(\frac{2}{0,2}=\frac{2}{\frac{2}{10}}=2 \times \frac{10}{2}=10\) | \(\frac{2}{0,5}=\frac{2}{\frac{5}{10}}=2\times \frac{10}{5}=4\) | \(\frac{2}{1}=2\) | \(\frac{2}{2}=1\) | \(\frac{2}{4}=0,5\) | \(\frac{2}{5}=0,4\) |
Question
2. Que peut-on dire des symétries de la courbe représentative de \(f\) ?
En déduire le tracé de la représentation graphique de \(f\) sur l'intervalle [-5 ; -0,1].
Solution
La courbe représentative de \(f\) est symétrique par rapport à l'origine du repère donc
le tracé de la représentation graphique de \(f\) sur l'intervalle [-5 ; -0,1] se déduit de celui des points du tableau précédent par symétrie par rapport à l'origine du repère.