Courbe deduite
Question
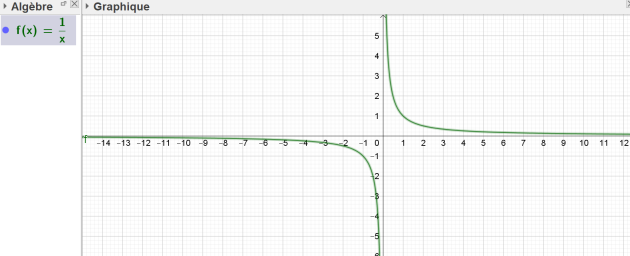
Tracer dans un repère orthonormal \((O;\mathbf{i};\mathbf{j} )\), la courbe C de la fonction \(\frac{1}{x}\)
Question
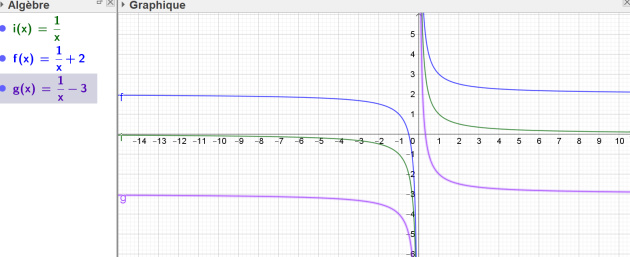
Les fonctions f et g sont définies par \(f(x)=\frac{1}{x}+2\) et \(g(x)=\frac{1}{x}-3\).
On appelle \(C_1\) et \(C_2\) leurs courbes représentatives.
a.Par quelle transformation passe-t-on de C à \(C_1\) ? de C à \(C_2\)?
b.Tracer \(C_1\) et \(C_2\)
Solution
Pour obtenir la courbe de f, on rajoute 2 aux ordonnées de celle de la fonction \(\frac{1}{x}\) donc il faut décaler de deux unités verticalement dans le sens des ordonnées croissantes la courbe représentative de la fonction \(\frac{1}{x}\)
Pour obtenir la courbe de g, on soustrait 3 aux ordonnées de celle de la fonction \(\frac{1}{x}\) donc il faut décaler de trois unités verticalement dans le sens des ordonnées décroissantes la courbe représentative de la fonction \(\frac{1}{x}\)
Question
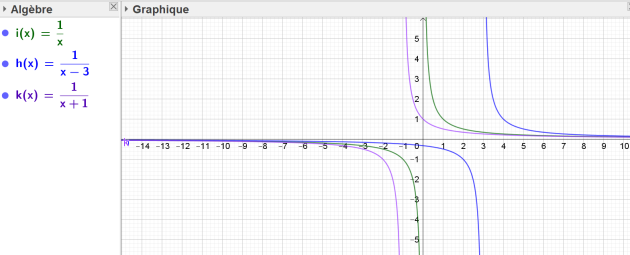
Les fonctions h et k sont définies par \(h(x)=\frac{1}{x-3}\) et \(k(x)=\frac{1}{x+1}\)
On appelle \(C_3\) et \(C_4\) leurs courbes représentatives.
a.Par quelle transformation passe-t-on de C à \(C_3\)? de C à \(C_4\) ?
b. Tracer \(C_3\) et \(C_4\)
Solution
Pour obtenir la courbe de h, il faut décaler de trois unités horizontalement dans le sens des abscisses croissantes la courbe représentative de la fonction \(\frac{1}{x}\)
Pour obtenir la courbe de k, il faut décaler de une unité horizontalement dans le sens des abscisses décroissantes la courbe représentative de la fonction \(\frac{1}{x}\)
Question
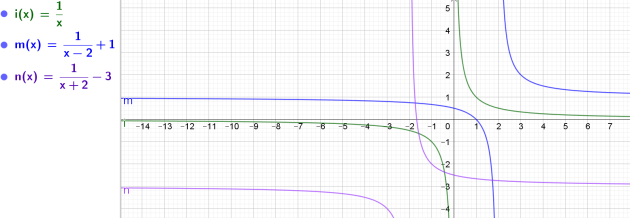
Les fonctions m et n sont définies par \(m(x)=\frac{1}{x-2}+1\)et \(n(x)=\frac{-3x-5}{x+2}\)
On appelle \(C_5\) et \(C_6\) leurs courbes représentatives.
a. Par quelle transformation passe-t-on de C à \(C_5\)? Tracer \(C_5\).
b.) Démontrer que \(n(x)=\frac{-3x-5}{x+2}=\frac{1}{x+2}-3\) En déduire le tracé de \(C_6\)
Solution
Pour obtenir la courbe de m, il faut décaler de deux unités horizontalement dans le sens des abscisses croissantes la courbe représentative de la fonction \(\frac{1}{x}\) pour obtenir la courbe représentative de la fonction \(\frac{1}{x-2}\) puis de une unité verticalement dans le sens des ordonnées croissantes la courbe représentative de la fonction \(\frac{1}{x-2}\)
\(\frac{1}{x+2}-3=\frac{1}{x+2}-3\frac{x+2}{x+2}=\frac{1-3(x+2)}{x+2}=\frac{1-3x-6}{x+2}=\frac{-3x-5}{x+2}\)
Pour obtenir la courbe de n, il faut décaler de deux unités horizontalement dans le sens des abscisses décroissantes la courbe représentative de la fonction \(\frac{1}{x}\) pour obtenir la courbe représentative de la fonction \(\frac{1}{x+2}\) puis de trois unités verticalement dans le sens des ordonnées décroissantes la courbe représentative de la fonction \(\frac{1}{x+2}-3\)