Exercice : Bibliotheque
Un étudiant peut emprunté au maximum un livre et un magazine.
Un bibliothécaire a constaté que :
– Lorsqu'un étudiant choisit un livre, ce livre est une bande dessinée avec une probabilité égale à 0,3 ou un roman une fois sur cinq ; sinon c'est un livre de cours.
– Lorsque l'étudiant choisit un roman, il prend aussi un magazine une fois sur deux.
– La probabilité qu'il emprunte à la fois une bande dessinée et un magazine est 0,24.
– Lorsqu'il prend un livre de cours, il n'emprunte pas de magazine.
Un étudiant entre dans la bibliothèque et emprunte un livre.
On notera :
B l'événement « il emprunte une bande dessinée » ;
R l'événement « il emprunte un roman » ;
C l'événement « il emprunte un livre de cours » ;
M l'événement « il emprunte un magazine »
Question
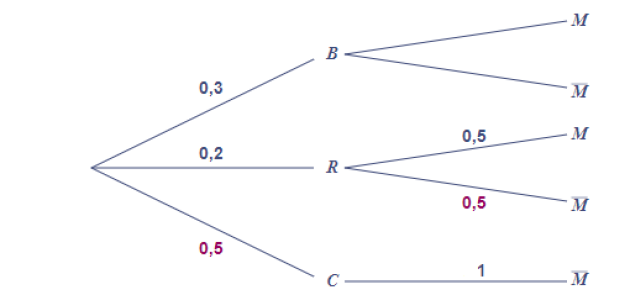
1. Construire un arbre de probabilités correspondant à cette situation.
Question
2. Calculer la probabilité qu'il choisisse un livre de cours.
Solution
p(B)+p(R)+p(C)=1 d'où p(C)=1−(0,3+0,2)=0,5
La probabilité qu'un étudiant choisisse un livre de cours est égale à 0,5.
Question
3. Calculer la probabilité qu'il emprunte un magazine sachant qu'il a déjà pris une bande dessinée.
Solution
\(p_R(M)=\frac{p(R∩M)}{p(R)}\) soit \(p_R(M)=\frac{0,24}{0,3}\)=0,8
La probabilité qu'un étudiant emprunte un magazine sachant qu'il a déjà pris une bande dessinée est égale à 0,8.
Question
4. Calculer la probabilité qu'il reparte avec un magazine.
Solution
Calculer la probabilité qu'il reparte avec un magazine.
Les évènements B, R et C déterminent une partition de l'ensemble des résultats de l'expérience aléatoire, alors d'après la formule des probabilités totales :
p(M)=p(B∩M)+p(R∩M)+p(C∩M)
Or p(C∩M)=0 et
p(R∩M)=\(p_R(M)\)×p(R).
Soit p(R∩M)=0,5 × 0,2=0,1.
D'où p(M)=0,24+0,1= 0,34
Ainsi, la probabilité qu'un étudiant reparte avec un magazine est égale à 0,34.
Question
5. Quelle est la probabilité qu'il emprunte un roman sachant qu'il a pris un magazine ?Le résultat sera arrondi au millième.
Solution
5.\(p_M(R)=\frac{p(R∩M)}{p(M)}\)
soit \(p_M(R)=\frac{0,1}{0,34}=\frac{5}{17}=\frac{5}{17}\simeq0,294\)
Arrondie au millième, la probabilité qu'un étudiant emprunte un roman sachant qu'il a pris un magazine est environ 0,294 soit environ 29,4 %.